21.2: Розбиття полів

Last updated
Save as PDF

Page ID: 64227

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

$F$Дозволяти$p(x)$ бути поле і бути непостійним многочленом в$F[x]\text{.}$ Ми вже знаємо, що ми можемо знайти розширення поля,$F$ що містить корінь з$p(x)\text{.}$ Однак, ми хотіли б знати, чи є розширення$E$$F$ містить всі корені$p(x)$ існує. Іншими словами, чи можемо ми знайти розширення поля$F$ таких, що$p(x)$ факторів у добуток лінійних многочленів? Що таке «найменша» розширення, що містить всі коріння$p(x)\text{?}$

$F$Дозволяти бути полем і$p(x) = a_0 + a_1 x + \cdots + a_n x^n$ бути непостійним многочленом в$F[x]\text{.}$ Поле розширення$E$ з$F$ є поле розщеплення,$p(x)$ якщо є елементи$\alpha_1, \ldots, \alpha_n$ в$E$ такому, що$E = F( \alpha_1, \ldots, \alpha_n )$ і

\[ p(x) = ( x - \alpha_1 )(x - \alpha_2) \cdots (x - \alpha_n)\text{.} \nonumber \]

Поліном$p(x) \in F[x]$ розщеплюється,$E$ якщо він є добутком лінійних факторів в$E[x]\text{.}$

Приклад$21.29$.

Нехай$p(x) = x^4 + 2x^2 - 8$ буде в${\mathbb Q}[x]\text{.}$ Тоді

Рішення

$p(x)$має$x^2 -2$ незведені фактори, і$x^2 + 4\text{.}$ тому поле${\mathbb Q}( \sqrt{2}, i )$ є розщеплюючим полем для$p(x)\text{.}$

Приклад$21.30$.

$p(x) = x^3 - 3$Дозволяти бути в${\mathbb Q}[x]\text{.}$ Тоді$p(x)$ має корінь в полі${\mathbb Q}( \sqrt[3]{3}\, )\text{.}$

Рішення

Однак це поле не є полем розщеплення,$p(x)$ оскільки складні кубові коріння 3,

\[ \frac{ -\sqrt[3]{3} \pm (\sqrt[6]{3}\, )^5 i }{2}\text{,} \nonumber \]

не в${\mathbb Q}( \sqrt[3]{3}\, )\text{.}$

Теорема$21.31$.

$p(x) \in F[x]$Дозволяти бути непостійним многочленом. Тоді існує поле розщеплення$E$ для$p(x)\text{.}$

Доказ

Ми будемо використовувати математичну індукцію на ступінь$p(x)\text{.}$ If$\deg p(x) = 1\text{,}$$p(x)$ то лінійний многочлен і$E = F\text{.}$ Припустимо, що теорема вірна для всіх поліномів ступеня$k$ з$1 \leq k \lt n$ і нехай$\deg p(x) = n\text{.}$ Ми можемо припустити, що$p(x)$ це не зводиться; інакше, по нашому індукційна гіпотеза, ми зробили. За теоремою існує$K$ таке поле$21.5$, яке$p(x)$ має нуль$\alpha_1$ в$K\text{.}$ Отже,$p(x) = (x - \alpha_1)q(x)\text{,}$ де$q(x) \in K[x]\text{.}$ Оскільки$\deg q(x) = n -1\text{,}$ існує поле$E \supset K$ розщеплення$q(x)$, що містить нулі$\alpha_2, \ldots, \alpha_n$ нашої$p(x)$ індукції гіпотеза. Отже,

\[ E = K(\alpha_2, \ldots, \alpha_n) = F(\alpha_1, \ldots, \alpha_n) \nonumber \]

є розщеплювальним полем$p(x)\text{.}$

Питання унікальності зараз виникає при розщепленні полів. На це питання відповідає ствердно. З урахуванням двох полів розщеплення$K$ та$L$ полінома$p(x) \in F[x]\text{,}$ існує ізоморфізм поля$\phi : K \rightarrow L$, який зберігає Для$F\text{.}$ того, щоб довести цей результат, ми повинні спочатку довести лему.

Теорема$21.32$.

$\phi : E \rightarrow F$Дозволяти ізоморфізм полів. $K$Дозволяти бути розширенням поля$E$ і$\alpha \in K$ бути алгебраїчним над$E$ з мінімальним многочленом$p(x)\text{.}$ Припустимо, що$\beta$ це поле розширення$F$ такого, що є коренем многочлена в$F[x]$$p(x)$ отриманому з-під зображення$L$ $\phi\text{.}$Потім$\phi$ поширюється на унікальний ізоморфізм$\overline{\phi} : E( \alpha ) \rightarrow F( \beta )$ такий, що$\overline{\phi}( \alpha ) = \beta$ і$\overline{\phi}$ погоджується з$\phi$ на$E\text{.}$

Доказ

Якщо$p(x)$ має ступінь,$n\text{,}$ то за теоремою$21.13$ ми можемо записати будь-який елемент у$E( \alpha )$ вигляді лінійної комбінації$1, \alpha, \ldots, \alpha^{n - 1}\text{.}$ Тому ізоморфізм, який ми шукаємо, повинен бути

\[ \overline{\phi}( a_0 + a_1 \alpha + \cdots + a_{n - 1} \alpha^{n - 1}) = \phi(a_0) + \phi(a_1) \beta + \cdots + \phi(a_{n - 1}) \beta^{n - 1}\text{,} \nonumber \]

де

\[ a_0 + a_1 \alpha + \cdots + a_{n - 1} \alpha^{n - 1} \nonumber \]

є елементом в$E(\alpha)\text{.}$ Той факт, що$\overline{\phi}$ це ізоморфізм можна перевірити шляхом прямого обчислення; однак легше спостерігати, що$\overline{\phi}$ це склад карт, які ми вже знаємо, як ізоморфізми.

Ми можемо$\phi$ поширюватися на ізоморфізм, від$E[x]$$F[x]\text{,}$ якого ми також позначимо, дозволивши$\phi\text{,}$

\[ \phi( a_0 + a_1 x + \cdots + a_n x^n ) = \phi( a_0 ) + \phi(a_1) x + \cdots + \phi(a_n) x^n\text{.} \nonumber \]

Це розширення узгоджується з оригінальним ізоморфізмом,$\phi : E \rightarrow F\text{,}$ оскільки постійні поліноми відображаються на постійні поліноми. За припущенням,$\phi(p(x)) = q(x)\text{;}$$\langle q(x) \rangle\text{.}$ отже,$\phi$ карти$\langle p(x) \rangle$ на Отже, ми маємо ізоморфізм$\psi : E[x] / \langle p(x) \rangle \rightarrow F[x]/\langle q(x) \rangle\text{.}$ За пропозицією$21.12$, ми маємо ізоморфізми$\sigma: E[x]/\langle p(x) \rangle \rightarrow E(\alpha)$ і$\tau : F[x]/\langle q(x) \rangle \rightarrow F( \beta )\text{,}$ визначаємо оцінкою в$\alpha$ і$\beta\text{,}$ відповідно. Тому$\overline{\phi} = \tau \psi \sigma^{-1}$ необхідний ізоморфізм (див. Рис.$21.33$).

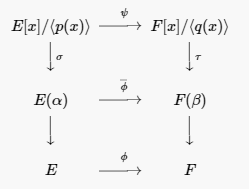
$clipboard_efac96b6fb89d79f1f30f7e405036f7a9.png$

$Figure \text { } 21.33.$

Ми залишаємо доказ унікальності як вправу.

Теорема$21.34$.

$\phi : E \rightarrow F$Дозволяти ізоморфізм полів і нехай$p(x)$ бути непостійним поліном в$E[x]$ і$q(x)$ відповідний поліном в$F[x]$ під ізоморфізмом. Якщо$K$ є розщеплювальним полем$p(x)$ і$L$ є полем розщеплення,$q(x)\text{,}$ то$\phi$ поширюється на ізоморфізм.$\psi : K \rightarrow L\text{.}$

Доказ

Ми будемо використовувати математичну індукцію на ступінь$p(x)\text{.}$ Ми можемо припустити, що$p(x)$ є нескорочуваним над$E\text{.}$ Отже, також$q(x)$ є нескоротним над$F\text{.}$ Якщо$\deg p(x) = 1\text{,}$ то за визначенням розщеплення поля,$K = E$$L = F$ і нічого не доводиться.

Припустимо, що теорема тримає для всіх поліномів ступеня менше, ніж$n\text{.}$ Оскільки$K$ є розщепленням поля$p(x)\text{,}$ всіх коренів$p(x)$ знаходяться в$K\text{.}$ Виберіть один з цих коренів, скажіть$\alpha\text{,}$ такий, що$E \subset E( \alpha ) \subset K\text{.}$ Аналогічно, ми можемо знайти корінь$\beta$$q(x)$ в $L$такий$21.32$, що$F \subset F( \beta) \subset L\text{.}$ За Леммою існує ізоморфізм$\overline{\phi} : E(\alpha ) \rightarrow F( \beta)$ такий, що$\overline{\phi}( \alpha ) = \beta$ і$\overline{\phi}$ погоджується з$\phi$ далі$E$ (див. Рис.$21.35$).

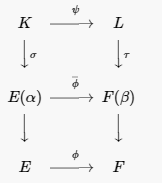
$clipboard_ed62e8e883f02c4e2e9f57520d6deda9f.png$

$Figure \text { } 21.35.$

Тепер пишемо$p(x) = (x - \alpha ) f(x)$ і$q(x) = ( x - \beta) g(x)\text{,}$ де$g(x)$ ступені$f(x)$ і менше ступенів$p(x)$ і$q(x)\text{,}$ відповідно. Розширення поля$K$ - це поле розщеплення для$f(x)$ понад$E( \alpha)\text{,}$ і$L$ є полем розщеплення для$g(x)$ понад$F( \beta )\text{.}$ За нашою індукційною гіпотезою існує ізоморфізм$\psi : K \rightarrow L$ такий, який$\psi$ узгоджується з$\overline{\phi}$ on$E( \alpha)\text{.}$ Отже, існує ізоморфізм$\psi : K \rightarrow L$ такий, що$\psi$ погоджується з$\phi$ на$E\text{.}$

Слідство$21.36$.

$p(x)$Дозволяти поліном в$F[x]\text{.}$ Тоді існує поле$K$ розщеплення$p(x)$, що є унікальним аж до ізоморфізму.