4.2.5: Загальні розв'язки трикутників
- Page ID
- 54622
Застосування теореми піфагора, тригонометричних функцій та законів синусов/косинусів.
Під час розмови з маленькою сестрою одного дня розмова перетворюється на форми. Ваша сестра тільки в молодшій школі, тому, хоча вона знає деякі речі про правильні трикутники, такі як теорема Піфагора, вона нічого не знає про інші типи трикутників. Ви показуєте їй приклад косого трикутника, намалювавши це на аркуші паперу:
Захоплюючись, вона каже вам, що знає, як обчислити площу трикутника, використовуючи звичну формулу\(\dfrac{1}{2} bh\) та довжини сторін, якщо трикутник є прямокутним трикутником, але що вона не може використовувати формули на щойно намалюваному трикутнику.
«Чи знаєте ви, як знайти довжини сторін трикутника і площі?» вона запитує.
Пошук розв'язків для трикутників
Пошук сторін, кутів та площі для прямокутних трикутників часто вивчається в Алгебрі та/або геометрії. Однак зазвичай можна дізнатися, як визначити цю інформацію в неправильних трикутниках в тригонометрії.
Нижче наведено діаграму, що підсумовує
поширені
прийоми трикутника. Ця діаграма описує тип трикутника (правий або косий), надану інформацію, відповідну техніку для використання та те, що ми можемо знайти, використовуючи кожну техніку.
| Тип трикутника: | Дана інформація: | Техніка: | Що ми можемо знайти: |
|---|---|---|---|
| Правий | Дві сторони | Теорема Піфагора | Третя сторона |
| Правий | Один кут і одна сторона | Тригонометричні коефіцієнти | Будь-яка з двох інших сторін |
| Правий | Дві сторони | Тригонометричні коефіцієнти | Будь-який з двох інших кутів |
| Косий | 2 кути і не включена сторона (AAS) | Закон Синеса | Інша сторона, що не входить |
| Косий | 2 кути і включена сторона (ASA) | Закон Синеса | Будь-яка з не включених сторін |
| Косий | 2 сторони і кут, протилежний одній з цих сторін (SSA) - Неоднозначний випадок | Закон Синеса | Кут, протилежний іншій стороні (може дати ні один, ні два рішення) |
| Косий | 2 сторони і включений кут (SAS) | Закон косинусів | третя сторона |
| Косий | 3 сторони | Закон косинусів | Будь-який з трьох |
| кути |
Розв'язування трикутників
1. В\(\Delta ABC\),\(a=12\),\(b=13\),\(c=8\). Розв'яжіть трикутник.
Так як нам дано всі три сторони в трикутнику, ми можемо використовувати Закон Косинуса. Перш ніж ми зможемо вирішити трикутник, важливо знати, якої інформації нам не вистачає. У цьому випадку ми не знаємо жодного з кутів, тому вирішуємо для\(\angle A\)\(\angle B\), і\(\angle C\). Почнемо з пошуку\(\angle A\):
\(\begin{aligned} 12^2 &=8^2+13^2−2(8)(13)\cos A\\ 144 &=233−208\cos A\\ −89 &=−208\cos A\\ 0.4278846154&=\cos A\\ 64.7&\approx \angle A \end{aligned}\)
Тепер ми знайдемо\ кут B, використовуючи Закон Косинусів. Майте на увазі, що тепер ви також можете використовувати Закон Сінеса, щоб знайти\(\angle B\). Використовуйте будь-який метод, з яким ви відчуваєте себе комфортніше.
\(\begin{aligned} 13^2 &=8^2+12^2−2(8)(12) \cos B\\ 169 &=208−192\cos B\\ −39 &=−192\cos B\\ 0.2031 &=\cos B\\ 78.3^{\circ} & \approx \angle B \end{aligned}\)
Тепер ми можемо швидко знайти,\(\angle C\) використовуючи теорему про суму трикутника,
\(180^{\circ} −64.7^{\circ} −78.3^{\circ} =37^{\circ}\)
2. У трикутнику\(DEF\)\(d=43\),\(e=37\),, і\(\angle F=124^{\circ} \). Розв'яжіть трикутник.
У цьому трикутнику ми маємо випадок SAS, оскільки ми знаємо дві сторони та включений кут. Це означає, що ми можемо використовувати Закон Косинусів для розв'язання трикутника. Для того щоб вирішити цей трикутник, нам потрібно знайти сторону\(f\)\(\angle D\), і\(\angle E\). Для початку нам потрібно буде знайти сторону,\(f\) використовуючи Закон Косинуса.
\ (\ почати {вирівняний}
f^ {2} &=43^ {2} +37^ {2} -2 (43) (37)\ cos 124\\
f^ {2} &=4997.351819\\
f &\ приблизно 70,7
\ кінець {вирівняний}\)
Тепер, коли ми знаємо\(f\), ми знаємо всі три сторони трикутника. Це означає, що ми можемо використовувати Закон Косинусів, щоб знайти\(\angle D\) або\(\angle E\). Ми знайдемо\(\angle D\) першим.
\ (\ почати {вирівняний}
43^ {2} &=70.7^ {2} +37^ {2} -2 (70.7) (37)\ cos D\\
1849 &= 6367.49-5231.8\ cos D\\
-4518.49 &= -5231.8\ cos D\\
0.863658779 &=\ cos D\\
30.3^ {\ circ}\ приблизно\ кут D
\ кінець {вирівняний}\)
Щоб знайти\(\angle E\), нам потрібно лише використовувати теорему про суму трикутника,\(\angle E=180−(124+30.3)=25.7^{\circ} \).
3. У трикутнику\(ABC\)\(A=43^{\circ} \),\(B=82^{\circ} \),, і\(c=10.3\). Розв'яжіть трикутник.
Це приклад випадку ASA, що означає, що ми можемо використовувати Закон Синеса для розв'язання трикутника. Для того, щоб використовувати Закон Синеса, ми повинні спочатку знати\(\angle C\), що ми можемо знайти, використовуючи теорему про суму трикутника,\(\angle C=180^{\circ} −(43^{\circ} +82^{\circ} )=55^{\circ} \).
Тепер, коли ми знаємо\(\angle C\), ми можемо використовувати Закон Синеса, щоб знайти будь-яку сторону а або сторону\(b\).
\ (\ почати {вирівняний}
\ розрив {\ sin 55} {10.3} & =\ гідророзриву {\ sin 43} {a} &\ frac {\ sin 55} {10.3} & =\ frac {\ sin 82} {\
a & =\ frac {10.3\ sin 43} {\ sin 55} & b & =\ frac {10.3\ sin 82\ син 55}\\
a & =8.6 & b & =12.5
\ кінець {вирівняний}\)
Раніше вас запитали, як ви можете допомогти своїй сестрі знайти довжини сторін і площу неправильного трикутника.
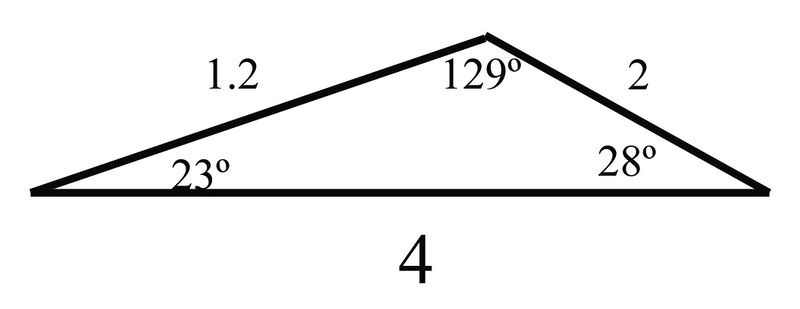
Рішення
Оскільки ви знаєте, що два кути - це\(23^{\circ} \) і\(28^{\circ} \), третій кут в трикутнику повинен бути\(180^{\circ} −23^{\circ} −28^{\circ} =129^{\circ} \). Використовуючи ці кути і знання про те, що одна зі сторін має довжину 4, можна вирішити для довжин двох інших сторін, використовуючи Закон Синусів:
\(\begin{aligned} \dfrac{\sin A}{a}&=\dfrac{\sin B}{b} \\ \dfrac{\sin 23^{\circ} }{a}&=\dfrac{\sin 129^{\circ} }{4} \\ a&=\dfrac{4 \sin 23^{\circ} }{\sin 129^{\circ} }=\dfrac{1.56}{.777} \\ a&\approx 2 \end{aligned}\)
І повторюємо процес для третьої сторони:
\(\begin{aligned} \dfrac{\sin A}{a}&=\dfrac{\sin C}{c} \\ \dfrac{\sin 23^{\circ} }{2}&= \dfrac{\sin 28^{\circ} }{c} \\ c&=\dfrac{2\sin 28^{\circ} }{\sin 23^{\circ} }=\dfrac{.939}{.781} \\ c&\approx 1.2 \end{aligned}\)
Тепер ви знаєте всі три кута і всі три сторони. Ви можете використовувати формулу Герона або альтернативну формулу площі трикутника, щоб знайти площу:
\(\begin{aligned} K&=\dfrac{1}{2} bc\sin A \\ K&=\dfrac{1}{2} (4)(1.2)\sin 23^{\circ} \\K&=\dfrac{1}{2}(4)(1.2)(.391) \\ K&\approx .9384 \end{aligned}\)
Використовуючи надану інформацію, вирішіть, в якому випадку вам надано (SSS, SAS, AAS, ASA або SSA), і чи будете ви використовувати Закон синусів або Закон косинусів, щоб знайти запитувану сторону або кут. Складіть приблизний креслення трикутника і позначте задану інформацію. Крім того, вкажіть, скільки рішень (якщо такі є) трикутник матиме. Якщо трикутник не має рішення або двох рішень, поясніть, чому.
Рішення
\(A=69^{\circ} \),\(B=12^{\circ} \),\(a=22.3\), знайти\(b\)
ААС, Закон Синеса, одне рішення
Використовуючи надану інформацію, вирішіть, в якому випадку вам надано (SSS, SAS, AAS, ASA або SSA), і чи будете ви використовувати Закон синусів або Закон косинусів, щоб знайти запитувану сторону або кут. Складіть приблизний креслення трикутника і позначте задану інформацію. Крім того, вкажіть, скільки рішень (якщо такі є) трикутник матиме. Якщо трикутник не має рішення або двох рішень, поясніть, чому.
Рішення
\(a=1.4\),\(b=2.3\),\(C=58^{\circ} \), знайти\(c\).
SAS, Закон косинусів, одне рішення
Використовуючи надану інформацію, вирішіть, в якому випадку вам надано (SSS, SAS, AAS, ASA або SSA), і чи будете ви використовувати Закон синусів або Закон косинусів, щоб знайти запитувану сторону або кут. Складіть приблизний креслення трикутника і позначте задану інформацію. Крім того, вкажіть, скільки рішень (якщо такі є) трикутник матиме. Якщо трикутник не має рішення або двох рішень, поясніть, чому.
Рішення
\(a=3.3\),\(b=6.1\),\(c=4.8\), знайти\(A\).
SSS, Закон косинусів, одне рішення
Рецензія
Використовуючи надану інформацію, вирішіть, в якому випадку вам надано (SSS, SAS, AAS, ASA або SSA), і чи будете ви використовувати Закон синусів або Закон косинусів, щоб знайти запитувану сторону або кут. Складіть приблизний креслення трикутника і позначте задану інформацію. Крім того, вкажіть, скільки рішень (якщо такі є) трикутник матиме.
- \(a=3\),\(b=4\),\(C=71^{\circ} \), знайти\(c\).
- \(a=8\),\(b=7\),\(c=9\), знайти\(A\).
- \(A=135^{\circ}\),\(B=12^{\circ} \),\(c=100\), знайти\(a\).
- \(a=12\),\(b=10\),\(A=80^{\circ} \), знайти\(c\).
- \(A=50^{\circ} \),\(B=87^{\circ}\),\(a=13\), знайти\(b\).
- В\(\Delta ABC\),\(a=15\),\(b=19\),\(c=20\). Розв'яжіть трикутник.
- В\(\Delta DEF\),\(d=12\),\(E=39^{\circ}\),\(f=17\). Розв'яжіть трикутник.
- В\(\Delta PQR\),\(P=115^{\circ} \),\(Q=30^{\circ} \),\(q=10\). Розв'яжіть трикутник.
- В\(\Delta MNL\),\(m=5\),\(n=9\),\(L=20^{\circ} \). Розв'яжіть трикутник.
- В\(\Delta SEV\),\(S=50^{\circ} \),\(E=44^{\circ} \),\(s=12\). Розв'яжіть трикутник.
- В\(\Delta KTS\),\(k=6\),\(t=15\),\(S=68^{\circ} \). Розв'яжіть трикутник.
- В\(\Delta WRS\),\(w=3\),\(r=5\),\(s=6\). Розв'яжіть трикутник.
- В\(\Delta DLP\),\(D=52^{\circ}\),\(L=110^{\circ} \),\(p=8\). Розв'яжіть трикутник.
- В\(\Delta XYZ\),\(x=10\),\(y=12\),\(z=9\). Розв'яжіть трикутник.
- В\(\Delta AMF\),\(A=99^{\circ}\),\(m=1\),\(f=16\). Розв'яжіть трикутник.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.12.
Лексика
| Термін | Визначення |
|---|---|
| закон косинусів | Закон косинусів - це правило, що стосується сторін трикутника з косинусом одного з його кутів. Закон косинусів говорить про те\(c^2=a^2+b^2−2ab\cos C\),\(C\) де кут поперек з боку\(c\). |
| закон синусів | Закон синусів - це правило, застосоване до трикутників, яке стверджує, що відношення синуса кута до сторони, протилежної цьому куту, дорівнює відношенню синуса іншого кута в трикутнику до сторони, протилежної цьому куту. |