Skip to main content
LibreTexts - Ukrayinska

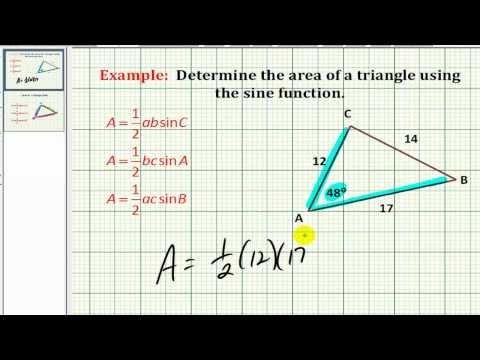
4.2.1: Формула площі для неправильних трикутників

  1. Last updated
  2. Save as PDF
  • Page ID
    54621

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Площа дорівнює половині добутку двох сторін і синусу включеного кута.

    Альтернативна формула для площі трикутника

    Ви вивчаєте Мексиканську затоку у своєму класі географії. Ваш інструктор виховує ідею Бермудського трикутника. Це місце, де, на думку деяких, багато літаків губляться. Ось ілюстрація цього:

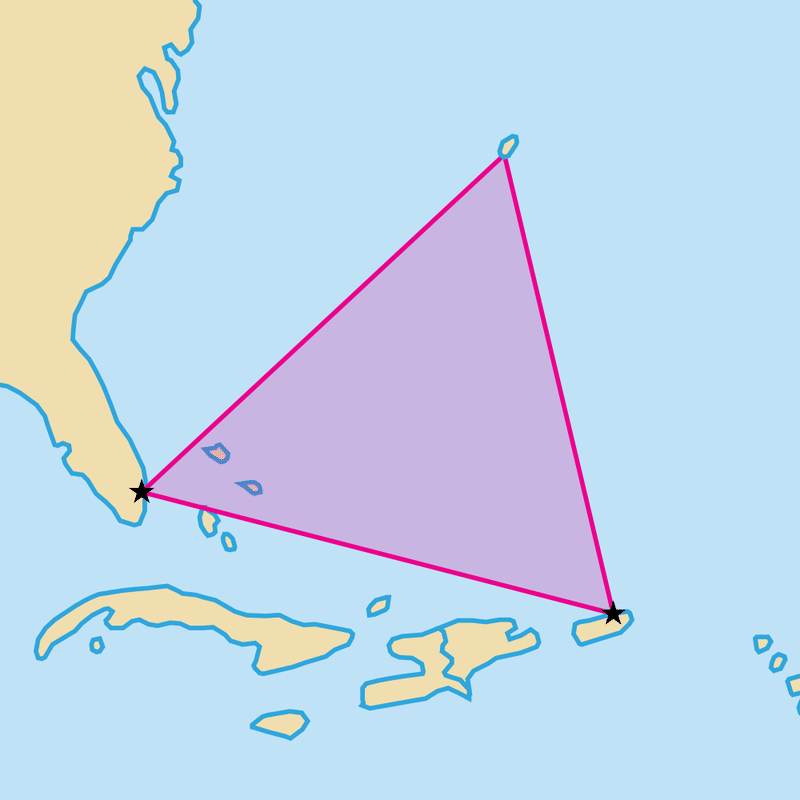
    Ф-д_230С6Д0ДА 4С10БА84С9Ф27ФЕ11А2Б103553878342226 БААФ 7Б57Д85+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Перше, що це змушує вас думати про ваш клас математики, оскільки цей клас є вашим улюбленим. Ви хотіли б знати, наскільки великий Бермудський трикутник. На жаль, Бермудський трикутник не є прямокутним трикутником. Однак ви знаєте, що довжина однієї зі сторін становить 950 миль, інша сторона - 975 миль, а кут між ними є\(60^{\circ} \).

    Чи є спосіб використовувати цю інформацію, щоб допомогти вам дізнатися, наскільки великий Бермудський трикутник?

    Площа трикутника

    У геометрії ви дізналися, що площа трикутника\(b\) є\(A=\dfrac{1}{2} bh\), де основа, а h - висота, або висота.

    Тепер, коли ви знаєте коефіцієнти трига, цю формулу можна змінити навколо, використовуючи синус.

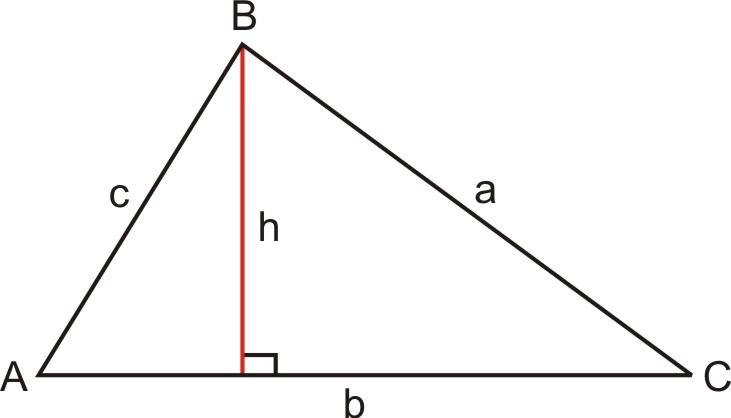
    Ф-Д_КК 75С0Д6С0ФБ4Б9Б54АФБ7191344Е400 БЕ29С75А50744А57А95904Ф+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{2}\)

    Дивлячись на трикутник вище, ви можете використовувати синус для визначення\(h\),\(\sin C=\dfrac{h}{a}\). Отже, вирішуючи це рівняння для\(h\), ми маємо\(a \sin C=h\). Підставивши це для\(h\), ми тепер маємо нову формулу для площі.

    \(A=\dfrac{1}{2} ab \sin C\)

    Це означає, що вам більше не потрібна висота, щоб знайти область. Все, що вам тепер потрібно, це дві сторони і кут між двома сторонами, називається включеним кутом.

    Знаходження області

    1.

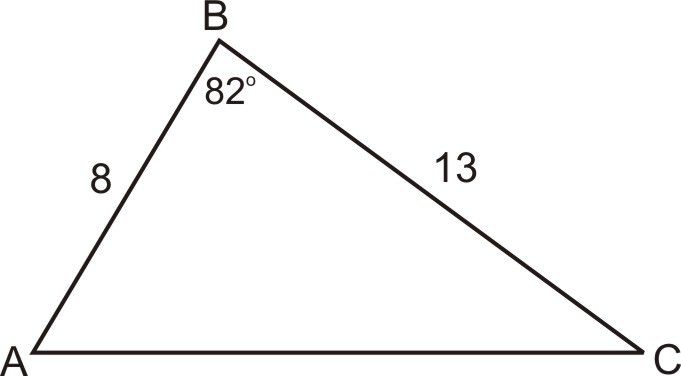
    Ф-Д_4Б05С0Ф082С77АА5054 ФДДДД715С132СБ6А 80Ф619А4ЕФ748Е532ДБ1+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{3}\)

    Використовуючи формулу\(A=\dfrac{1}{2} ab \sin C\), ми маємо

    \(\begin{aligned} A&=\dfrac{1}{2} \cdot 8\cdot 13\cdot \sin 82^{\circ} \\ &=4\cdot 13\cdot 0.990\\ &=51.494 \end{aligned}\)

    2.

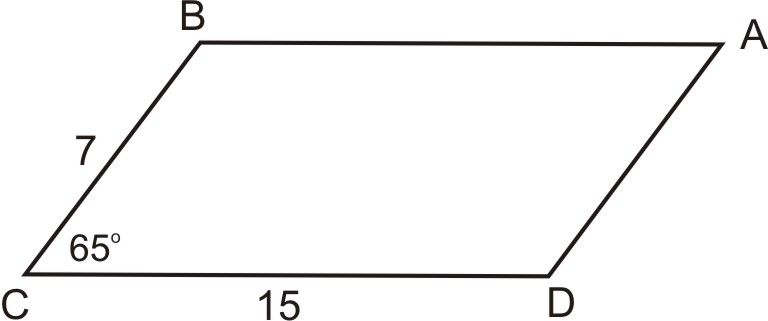
    Ф-д_А1С4Б8ФД6Д9А1648 АЕ082406357361 ДФ 607021867А8А7А7А7Е31Е8+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{4}\)

    Нагадаємо, що паралелограм можна розділити на два трикутника. Таким чином, формула для паралелограма, використовуючи нову формулу, буде:\(A=2\cdot \dfrac{1}{2} ab \sin C\) або\(A=ab \sin C\).

    \(\begin{aligned} A&=7\cdot 15\cdot \sin 65^{\circ} \\&=95.162 \end{aligned} \)

    3.

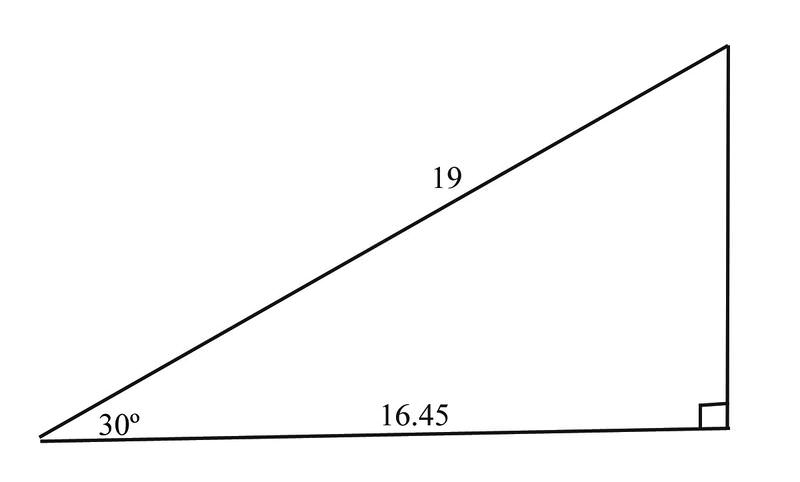
    F-д_615АС6Е69 ЕСД 2424С48ЕБ387Д55 Фе 7270Б0Б0154Б1Б26С143FCED7EB8+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{5}\)

    Використовуючи формулу\(A=\dfrac{1}{2} ab \sin C\), ми маємо

    \(\begin{aligned} A&=\dfrac{1}{2} \cdot 16.45\cdot 19\cdot \sin 30^{\circ} \\ &=8.225\cdot 19\cdot 0.5 \\&=78.14\end{aligned}\)

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, наскільки великий Бермудський трикутник.

    Рішення

    Тепер, коли ви знаєте рівняння для площі трикутника через дві сторони та включений кут, ми можемо використовувати це для вирішення площі Бермудського трикутника:

    \(\begin{aligned} A&=\dfrac{1}{2} ab \sin\theta \\ A&=\dfrac{1}{2} (950)(975) \sin 60^{\circ} \\ A&=\dfrac{1}{2} (950)(975)(.866) \\ A&=401066.25\end{aligned}\)

    Площа трикутника становить приблизно 401,006 квадратних миль.

    Приклад\(\PageIndex{2}\)

    Знайдіть площу трикутника.

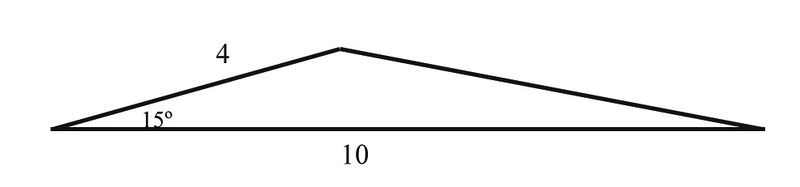
    Ф-Д_9ДАА 59ДФ 286Д734Е460087 АБ792 Ф1Б13Б8СЕ5А5А1295Б0А038СБ6+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{6}\)

    Рішення

    Використовуючи формулу\(A=\dfrac{1}{2} ab \sin C\), ми маємо

    \(\begin{aligned} A&=\dfrac{1}{2} \cdot 4\cdot 10\cdot \sin 15^{\circ} \\ &=2\cdot 10\cdot 0.2589 \\ &=5.178 \end{aligned} \)

    Приклад\(\PageIndex{3}\)

    Знайдіть площу трикутника.

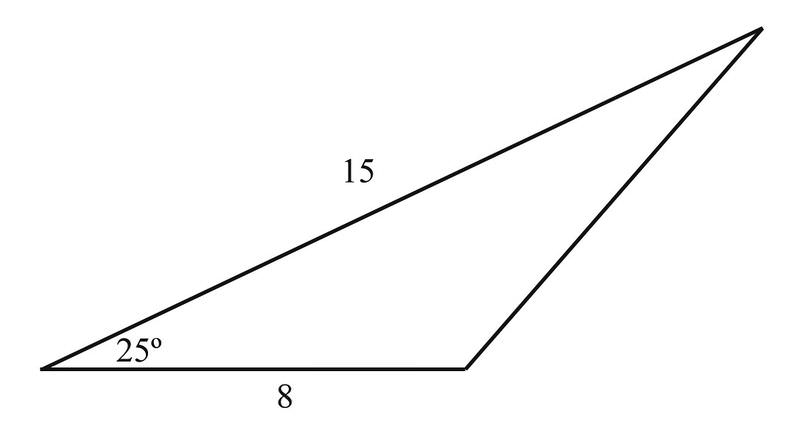
    Ф-Д_076А7990А2ФБ9Б9ББ 16706Ф1С056724Ф42Е4ДФ51ЕАА1С793С02Б13Е617+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{7}\)

    Рішення

    Використовуючи формулу\(A=\dfrac{1}{2} ab \sin C\), ми маємо

    \(\begin{aligned} A&=\dfrac{1}{2}\cdot 8\cdot 15\cdot \sin 25^{\circ} \\ &=4\cdot 15\cdot 0.4226\\ &=25.356 \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть площу трикутника.

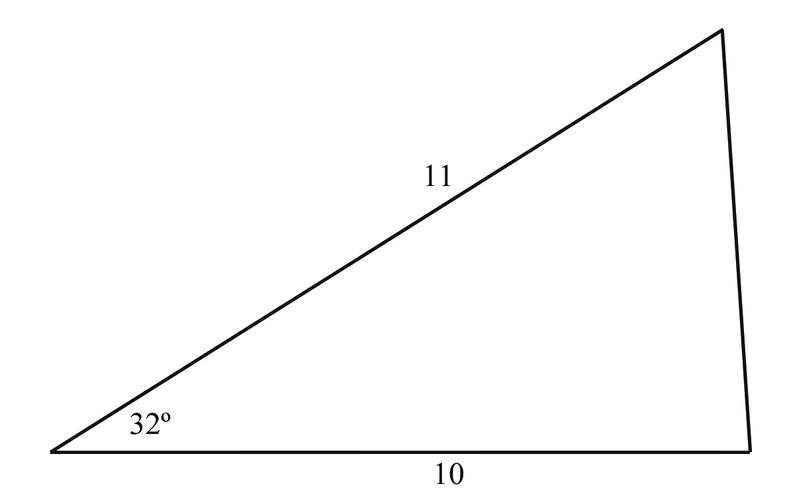
    Ф-Д_0А7473ФБ821537А58389 ДБ5 ЕАБ 483Д2Б09Е0Е3ФФ0Б2БАФД 60АЕ5+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{8}\)

    Рішення

    Використовуючи формулу\(A=\dfrac{1}{2} ab \sin C\), ми маємо

    \(\begin{aligned} A&=\dfrac{1}{2} \cdot 10\cdot 11\cdot \sin 32^{\circ} \\&=5\cdot 11\cdot 0.53 \\ &=29.15 \end{aligned}\)

    Рецензія

    Використовуйте наступну картинку для питань 1 і 2.

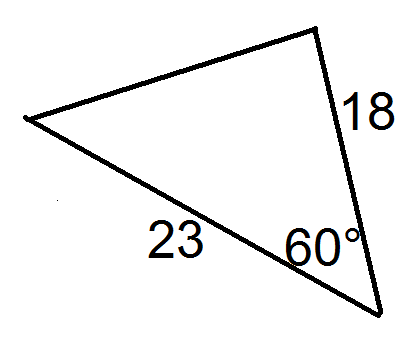
    F-д_д7а 9671 БК 150056DA0A498d6c5677905213d4f70d1a6d82b25910+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)
    1. Знайдіть значення\(a\)\(b\), і\(C\) необхідні для формули, щоб знайти площу трикутника.
    2. Тепер знайдіть площу трикутника.

    Використовуйте наступну картинку для питань 3 і 4.

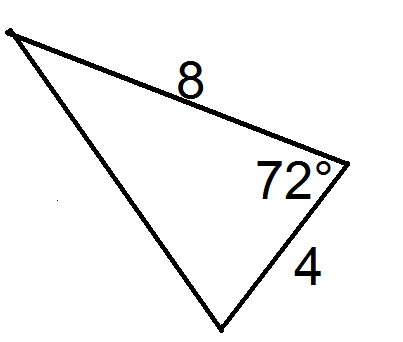
    F-D_CEDEA 896 КДС514Б74 ЕАФ 10027059036Б768Б596 ФК594206408493D41+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)
    1. Знайдіть значення\(a\)\(b\), і\(C\) необхідні для формули, щоб знайти площу трикутника.
    2. Тепер знайдіть площу трикутника.

    Знайдіть площу кожного трикутника нижче.


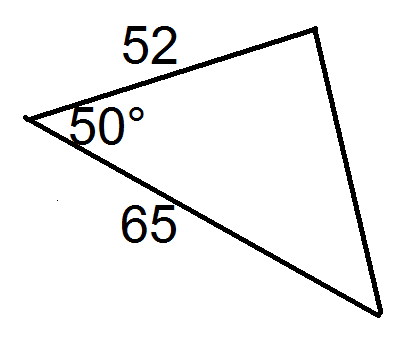
    1. Ф-Д_Б02А0С410Е73Ф281269864Ф92553Д458С9КС647ЕБ68712ДБК36А952С+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{11}\)
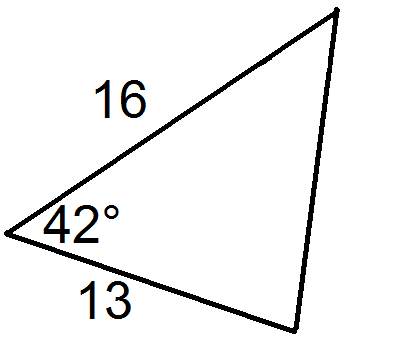
    2. Ф-д_78Б2Ф9Б7А8Е921С632Е883Д8Е4АААБК 2782C0E628FA0890281591535+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
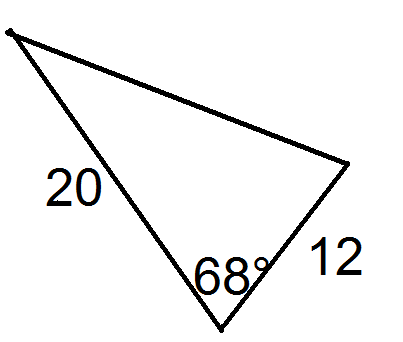
    3. F-D_1C9 АЦФ 952CFDB70CFFA 90Б9Б16614 АД 4659829Б45БК 70Ф9С22574 ДД41+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
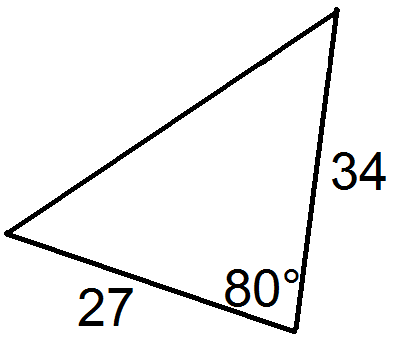
    4. F-д_д1е382АААА Е511С02Б86Д0АД 8Б97070С98Б838Б418502950E2C8C113E+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
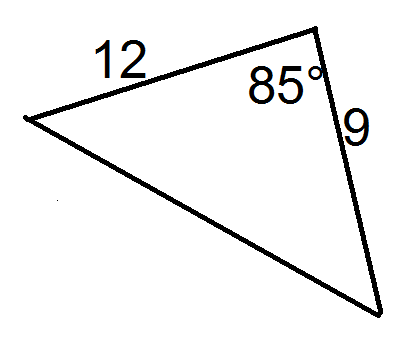
    5. F-D_5C252A3D7D9948 АФ 388ДА049Ф5С499Е021А445Е5Д3926A117EF55089+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
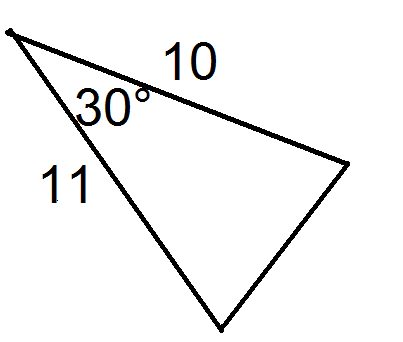
    6. F-D_ЕЦ9БА 4270С2Б6А0602А02Д4Д34 Даба743Е3Ф2А51CE813196A88A3FF+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
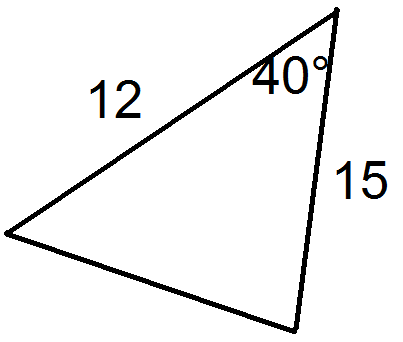
    7. F-D_1866 Фе 5 ДБ4 ФС8 ФЧ 8С30ДФ Ф 1995 А88КС6Б5Д49040E2488023 BE5C+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)

    Знайдіть площу кожного паралелограма.


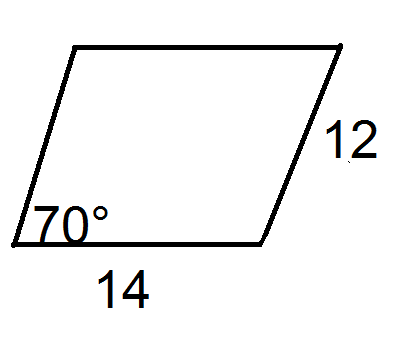
    1. F-D_D41628A214D Дек 200E8D2557260 ДК836Б11 ЕЕБ 277D1D8ADFF01E0E5E+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
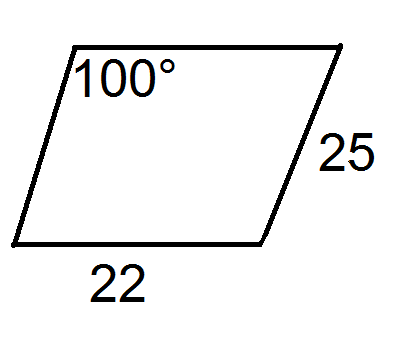
    2. Ф-д_4904020 ФБ31ФЕ 8Ф0С9Б066А 5874Е9 АБ 3ЕФД Д 4Ф6729 ЕД6СЕФ864Д01С+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
    3. Опишіть інший спосіб, яким ви могли б знайти площу паралелограма в попередній задачі.
    4. Коли ви вперше дізналися про синус, ви дізналися, як це працює для правильних трикутників. Поясніть, чому цей метод обчислення площі використовує синус, але працює для неправильних трикутників.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.12.

    Лексика

    Термін Визначення
    У комплекті Кут Вхідний кут в трикутник - це кут між двома відомими сторонами.
    синус Синус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину гіпотенузи.