4.2.4: Формула Герона

Формула площі заснована на довжині сторін трикутника і половини його периметра.

Сарін малює трикутник і вимірює його сторони як 2 дюйми, 5 дюймів і 6 дюймів. Яка площа її трикутника?

Формула чаплі

Формула Герона, названа на честь героя Олександрії 2000 років тому, може бути використана для пошуку площі трикутника з урахуванням трьох довжин сторін. Формула вимагає напівпериметра$s$, або$\dfrac{1}{2}(a+b+c)$$a$, де$c$,$b$ і - довжини сторін трикутника.

Формула чаплі:

$\text{Area}=\sqrt{s(s−a)(s−b)(s−c)}$

Скористаємося формулою Герона, щоб знайти площу трикутника з довжинами сторін 13 см, 16 см і 23 см.

Спочатку знайдіть напівпериметр або$s$:$s=\dfrac{1}{2}(13+16+23)=26$. Далі підставляємо наші значення в формулу, як показано на малюнку, і оцінюємо:

$A=\sqrt{26(26−13)(26−16)(26−23)}=\sqrt{26(13)(10)(3)}=\sqrt{10140}\approx 101 \text{ cm}^2$

Тепер давайте відповімо на наступні питання.

1. Олена планує сад у своєму дворі. Вона використовує три шматки дерева в якості бордюру. Якщо шматки дерева мають довжину 4 футів, 6 футів і 3 футів, яка площа її саду?

Сад буде трикутним з довжиною сторін 4 фути, 6 футів і 3 футів. Знайдіть напівпериметр, а потім скористайтеся формулою Герона, щоб знайти площу.

$\begin{aligned} s&=\dfrac{1}{2}(4+6+3)=\dfrac{13}{2} \\ A&=\sqrt{\dfrac{13}{2}\left(\dfrac{13}{2}−4\right)\left(\dfrac{13}{2}−6\right)\left(\dfrac{13}{2}−3\right)}=\sqrt{\dfrac{13}{2} \left(\dfrac{5}{2}\right) \left(\dfrac{1}{2}\right)\left(\dfrac{7}{2}\right)}=\sqrt{\dfrac{455}{16}} \approx 28 \text{ ft}^2 \end{aligned}$

2. Керолайн хоче виміряти висоту радіовежі. З деякої відстані від вежі кут піднесення від її місця до вершини вежі становить$65^{\circ}$. Керолайн йде на 100 м далі від вежі і вимірює кут піднесення до вершини вежі, щоб бути$48^{\circ}$. Наскільки висока вежа?

Малюнок$\PageIndex{1}$

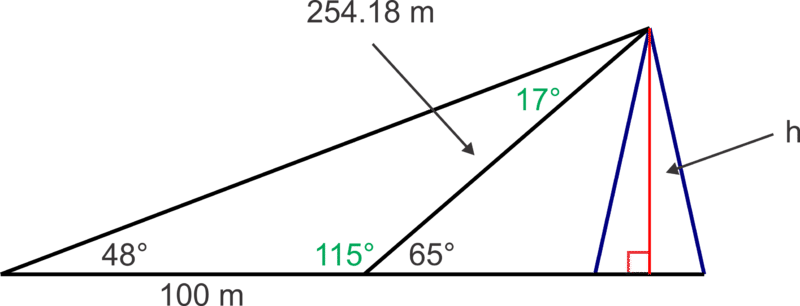
Для початку складіть схему, щоб проілюструвати ситуацію.

Ми можемо використовувати властивості кута (лінійна пара та сума трикутника), щоб знайти кути, показані зеленим кольором на діаграмі.

$180^{\circ} −65^{\circ} =115^{\circ}$і$180^{\circ} −48^{\circ} −115^{\circ} =17^{\circ}$

Далі ми можемо використовувати Закон синусів у тупому трикутнику, щоб знайти гіпотенузу в прямокутному трикутнику:

$\begin{aligned} \dfrac{\sin 17^{\circ} }{100} =\dfrac{\sin 48^{\circ} }{x} \\ x=\dfrac{100 \sin 48^{\circ}}{ \sin 17^{\circ} } \approx 254.18 \end{aligned}$

Нарешті, ми можемо використовувати співвідношення синусів у прямокутному трикутнику, щоб знайти висоту вежі:

$\sin 65^{\circ} =\dfrac{h}{254.18}$,$h=254.18\sin 65^{\circ} \approx 230.37 \text{ m}$

Приклад$\PageIndex{1}$

Раніше вас попросили знайти площу трикутника зі сторонами довжиною 2 дюйми, 5 дюймів і 6 дюймів.

Рішення

Спочатку знайдіть напівпериметр або s:$s=\dfrac{1}{2}(2+5+6)=6.5$. Далі підставляємо наші значення в формулу Герона і оцінюємо:

$A=\sqrt{6.5(6.5−2)(6.5−5)(6.5−6)}=\sqrt{6.5(4.5)(1.5)(0.5)}=\sqrt{21.94} \approx 4.7 \text{ in.}^2$

Використовуйте найбільш підходяще правило або формулу (Закон Синуса, Закон Косинуса, Формула площі з синусом або формула Герона), щоб відповісти на наступні питання.

Приклад$\PageIndex{2}$

Знайти площу трикутника з довжинами сторін 50 м, 45 м і 25 м.

Рішення

Формула чаплі:

$s=\dfrac{1}{2} (50+45+25)=60$,$A=\sqrt{60(60−50)(60−45)(60−25)} \approx 561 \text{ m}^2$.

Приклад$\PageIndex{3}$

Метью планує удобрювати свою траву. Кожен мішок добрива претендує на покриття 500 кв. футів трави. Його власність землі приблизно має форму трикутника. Він вимірює дві сторони свого двору, щоб бути 75 футів і 100 футів, а кут між ними є$72^{\circ}$. Скільки мішків з добривом він повинен купити?

Рішення

Формула площі з синусом:$\dfrac{1}{2} (75)(100)\sin 72^{\circ} \approx 3566 \text{ ft }^2$, Кількість мішків$\dfrac{3566}{500} \approx 7.132\approx 8 \text{ bags}$. Ми округляємо, тому що 7 мішків не зовсім достатньо.

Приклад$\PageIndex{4}$

Пара сусідніх сторін в паралелограмі 3 в і 7 в і кут між ними дорівнює$62^{\circ}$, знайти довжину діагоналей.

Малюнок$\PageIndex{2}$

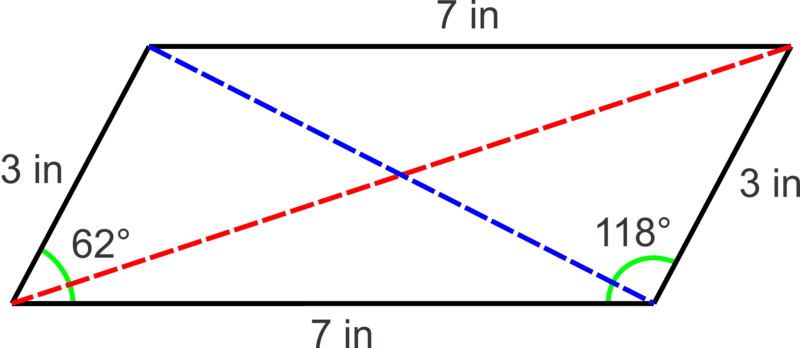
Рішення

Закон Косинуса, щоб знайти синю діагональ:

$\begin{aligned} c^2&=3^2+7^2−2(3)(7)\cos 62^{\circ} \\ c&=\sqrt{38.28}\approx 6.19 \end{aligned}$

Отже, 6.19 в

Щоб знайти зелену діагональ, ми можемо використовувати Закон Косинусів з сусіднім кутом$180^{\circ} −62^{\circ} −118^{\circ}$:

$\begin{aligned} c^2 &=7^2+3^2−2(7)(3)\cos 118^{\circ} \\ c&=\sqrt{77.72} \approx 8.82 \end{aligned}$

Отже, 8.82 в

Рецензія

Використовуйте Закон Синуса, Закон Косинуса, Площа трикутника з синусом або Формулу Герона для вирішення реальних завдань застосування.

1. Два спостерігача, Рейчел і Луїс, стоять на березі, в 0,5 км один від одного. Кожен з них вимірює кут між береговою лінією і вітрильником, що виходить на воду одночасно. Якщо кут Рейчел$63^{\circ}$ і кут Луїса дорівнює$56^{\circ}$, знайдіть відстань між Луїсом і вітрильником до найближчої сотої милі.
2. Двоє пішоходів ходять від протилежних кінців міського кварталу до точки з іншого боку вулиці. Кут, утворений їх доріжками, є$125^{\circ}$. Один пішохід ходить 300 футів, а інший - 320 футів. Як довго знаходиться міський квартал до найближчої ноги?
3. Дві сторони і включений кут паралелограма мають розміри 3,2 см, 4,8 см і$54.3^{\circ}$ відповідно. Знайдіть довжини діагоналей до найближчої десятої частини сантиметра.
4. Міст підтримується трикутними розкосами. Якщо сторони кожної дужки мають довжину 63 футів, 46 футів і 40 футів, знайдіть міру найбільшого кута до найближчого градуса.
5. Знайдіть трикутну ділянку, до найближчого квадратного метра, обнесену трьома шматками огорожі довжиною 123 м, 150 м і 155 м.
6. Знайдіть площу, до найближчого квадратного дюйма, паралелограма зі сторонами довжиною 12 дюймів і 15 дюймів і включеним кутом$78^{\circ}$.
7. Людина в точці$A$ дивиться через схід і помічає НЛО з кутом піднесення$40^{\circ}$. У той же час інша людина, в 1 милі на захід від А дивиться на схід і оглядає той же НЛО з кутом піднесення$25^{\circ}$. Знайти відстань між А і НЛО. Як далеко знаходиться НЛО над землею? Дайте відповіді на найближчу соту милю.
8. Знайдіть площу трикутної майданчика, до найближчого квадратного метра, зі сторонами довжиною 10 м, 15 м і 16 м.
9. Двір обмежений з двох сторін огорожами довжиною 80 футів і 60 футів. Якщо ці огорожі зустрічаються під$75^{\circ}$ кутом, скільки футів огорожі потрібно, щоб повністю закрити трикутну область?
10. Коли хлопчик стоїть на березі річки і дивиться поперек на інший берег, кут западини$12^{\circ}$. Якщо він піднімається на вершину 10-футового дерева і дивиться поперек на інший берег, кут западини дорівнює$15^{\circ}$. Яка відстань від першої позиції хлопчика до іншого берега річки? Наскільки широка річка? Дайте свої відповіді найближчій нозі.

Відповіді на проблеми з оглядом

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 13.17.

Додаткові ресурси

Відео: Формула площі чаплі - приклад 1