2.6.6: Амплітуда

Вимірювання висоти хвилі від центральної осі.

Амплітуда синусоїдальної і косинусної функцій - це вертикальна відстань між синусоїдальної віссю і максимальним або мінімальним значенням функції. По відношенню до звукових хвиль амплітуда - це міра того, наскільки голосно щось.

Яка найпоширеніша помилка, допущена при графіку амплітуди синусоїди?

Амплітуда синусоїдальних функцій

Загальна форма синусоїдальної функції - це:

$f(x)=\pm a\cdot \sin (b(x+c))+d$

Функцію косинуса можна так само легко підставити, і для багатьох завдань буде простіше використовувати рівняння косинуса. оскільки і синусоїдальні, і косинусні хвилі ідентичні за винятком горизонтального зсуву, все залежить від того, де ви бачите хвилю, що починається.

Коефіцієнт а - амплітуда. Коли немає числа, то амплітуда дорівнює 1. Найкращий спосіб визначити амплітуду - це зображення. Нижче наведено графік функції$f(x)=3\cdot \sin x$, яка має амплітуду 3.

Малюнок$\PageIndex{1}$

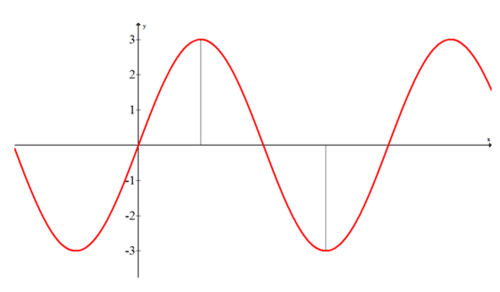
Зверніть увагу, що амплітуда дорівнює 3, а не 6. Це відповідає абсолютному значенню максимального і мінімального значень функції. Якби функція була$f(x)=−3\cdot \sin x$, то весь графік буде відображатися по осі x.

Також зверніть увагу, що вісь x на графіку вище не позначена. Це показує, що амплітуда - це вертикальна відстань. Синусоїдальна вісь - це нейтральна горизонтальна лінія, яка лежить між гребенями і западинами (або піками і долинами, якщо ви віддаєте перевагу). Для цієї функції синусоїдальна вісь була лише віссю x, але якби весь графік був зміщений вгору, синусоїдальна вісь більше не була б віссю x. Натомість це все одно буде горизонтальна лінія безпосередньо між гребенями та коритами, яка також є середнім значенням максимального та мінімального значень.

Перегляньте частину цього відео, обговорюючи амплітуду:

Приклад$\PageIndex{1}$

Раніше вас запитали про найпоширенішу помилку, допущену при графіку амплітуди однієї хвилі. Найпоширеніша помилка - подвоєння або вдвічі зменшення амплітуди без необхідності.

Рішення

Раніше вас запитали про найпоширенішу помилку, допущену при графіку амплітуди однієї хвилі. Найпоширеніша помилка - подвоєння або вдвічі зменшення амплітуди без необхідності.

Приклад$\PageIndex{2}$

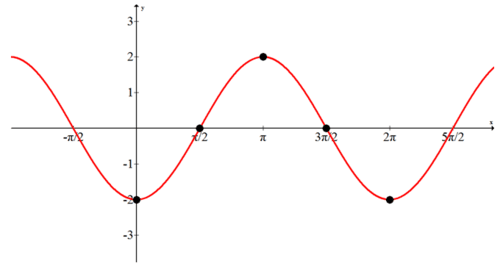
Графік наступної функції шляхом побудови основних пунктів:$f(x)=−2\cdot \cos x$.

Рішення

Амплітуда дорівнює 2, а значить максимальні значення будуть на рівні 2, а мінімальні - на -2. Зазвичай з базовою кривою косинуса точки, що відповідають 0$\dfrac{\pi }{2}$$\pi$,$\dfrac{3\pi }{2}$,,,$2\pi$ падають вище, на або нижче лінії в наступній послідовності: вище, на, внизу, на, вище. Негативний знак у рівнянні перемикається вище на нижче і знизу з вище. Весь графік відбивається по осі x.

Малюнок$\PageIndex{2}$

Приклад$\PageIndex{3}$

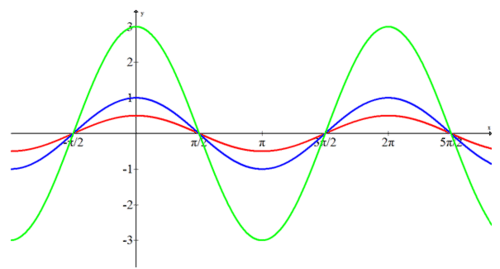
Напишіть рівняння косинуса для кожної з наступних функцій.

Малюнок$\PageIndex{3}$

Рішення

Амплітуди трьох функцій 3, 1$\dfrac{1}{2}$ і жодна з них не відображається по осі x.

$\begin{aligned} f(x)&=3\cdot \cos x \\ h(x)&=\cos x \\ g(x)&=\dfrac{1}{2}\cdot \cos x \end{aligned}$

Зверніть увагу, що сама по собі амплітуда завжди позитивна.

Приклад$\PageIndex{4}$

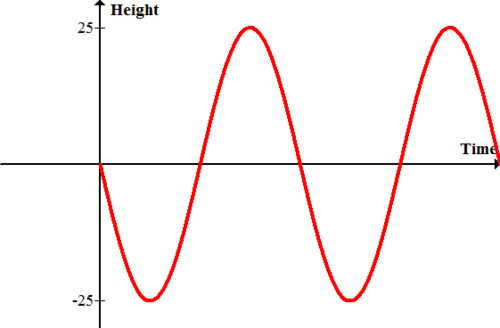
Колесо огляду радіусом 25 футів сидить поруч з платформою. Поїздка починається на платформі і їде вниз, щоб почати. Модель висоти в порівнянні з часом їзди.

Рішення

оскільки немає інформації про час, просто позначте вісь x як час. За часом нуль висота дорівнює нулю. Спочатку висота буде зменшуватися в міру того, як їзда йде нижче платформи. В кінцевому підсумку колесо знайде мінімум і почне збільшуватися знову до кінця, поки не досягне максимуму.

Малюнок$\PageIndex{4}$

Приклад$\PageIndex{5}$

Знайдіть амплітуду функції$f(x)=−3\cos x$ і використовуйте мову перетворень, щоб описати, як графік пов'язаний з батьківською функцією$y=\cos x$.

Рішення

Нова функція відбивається по осі x і вертикально розтягується в 3 рази.

Малюнок$\PageIndex{5}$

Рецензія

1. Поясніть, як знайти амплітуду синусоїдальної функції з її рівняння.
2. Поясніть, як знайти амплітуду синусоїдальної функції з її графіка.

Знайдіть амплітуду кожної з наступних функцій.

3. $g(x)=−5\cos x$

4. 

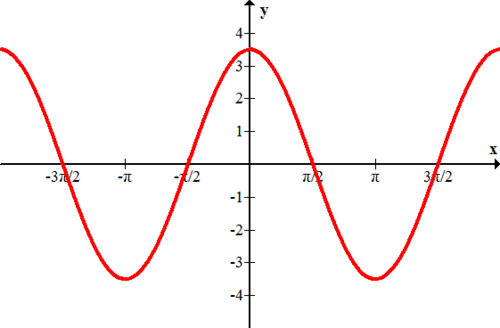
   Малюнок$\PageIndex{6}$

5. $f(x)=\dfrac{1}{2} \sin x$

6. 

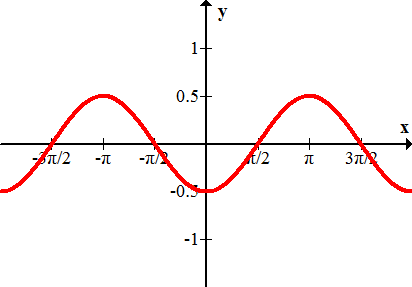
   Малюнок$\PageIndex{7}$

7. $j(x)=3.12\cos x$

8. 

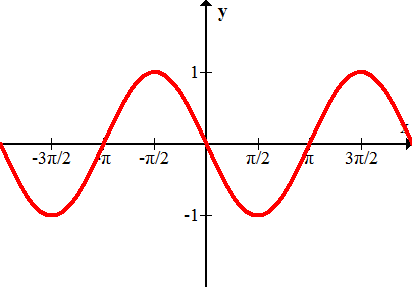
   Малюнок$\PageIndex{8}$

Намалюйте кожну з наступних функцій.

9. $f(x)=3\sin x$

10. $g(x)=−4\cos x$

11. $h(x)=\pi \sin x$

12. $k(x)=−1.2\cos x$

13. $p(x)=\dfrac{2}{3} \cos x$

14. $m(x)=−\dfrac{1}{2} \sin x$

15. Попередній перегляд:$r(x)=3\sin x+2$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.3.

Додаткові ресурси

Відео: Амплітуда і період синуса і косинуса