5.3: Амплітуда синусоїдальних функцій
- Page ID
- 54662
Амплітуда синусоїдальної і косинусної функцій - це вертикальна відстань між синусоїдальної віссю і максимальним або мінімальним значенням функції. По відношенню до звукових хвиль амплітуда - це міра того, наскільки голосно щось.
Яка найпоширеніша помилка, допущена при графіку амплітуди синусоїди?
Амплітуда синусоїдальних функцій
Загальна форма синусоїдальної функції - це:
f (x) =\ пм а\ cdot\ sin (б (х+с)) +д
Функцію косинуса можна так само легко підставити, і для багатьох завдань буде простіше використовувати рівняння косинуса. Оскільки і синусоїди, і косинуси однакові, за винятком горизонтального зсуву, все залежить від того, де ви бачите хвилю, що починається.
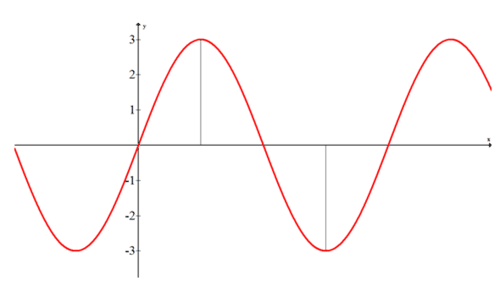
Коефіцієнт\(a\) - амплітуда. Коли немає числа, тоді амплітуда -\(1 .\) найкращий спосіб визначити амплітуду - це зображення. Нижче наведено графік функції,\(f(x)=3 \cdot \sin x,\) яка має амплітуду 3.
Зверніть увагу, що амплітуда дорівнює 3, а не 6. Це відповідає абсолютному значенню максимального і мінімального значень функції. Якби функція була,\(f(x)=-3 \cdot \sin x,\) то весь графік буде відображатися поперек\(x\) осі.
Також зверніть увагу, що\(x\) вісь на графіку вище не позначена. Це показує, що амплітуда - це вертикальна відстань. Синусоїдальна вісь - це нейтральна горизонтальна лінія, яка лежить між гребенями і западинами (або піками і долинами, якщо ви віддаєте перевагу). Для цієї функції синусоїдальна вісь була лише\(x\) віссю, але якби весь графік був зміщений вгору, синусоїдальна вісь більше не була б\(x\) віссю. Натомість це все одно буде горизонтальна лінія безпосередньо між гребенями та коритами, яка також є середнім значенням максимального та мінімального значень.
Перегляньте частину цього відео, обговорюючи амплітуду:
Приклади
Раніше вас запитали про найпоширенішу помилку, допущену при графіку амплітуди однієї хвилі. Найпоширеніша помилка - подвоєння або вдвічі зменшення амплітуди без необхідності. Багато хто забуває, що число\(a\) в рівнянні, як і 3 в\(f(x)=3 \sin x\), - це відстань від\(x\) осі як до піку, так і до долини. Це не загальна відстань від вершини до долини.
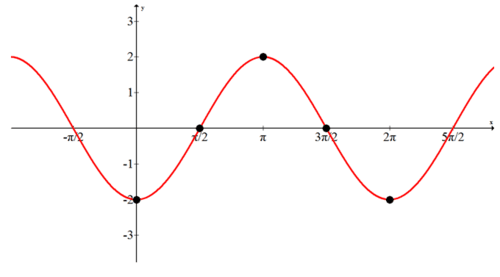
Графік наступної функції шляхом побудови основних пунктів:\(f(x)=-2 \cdot \cos x\).
Амплітуда дорівнює 2, а значить максимальні значення будуть на рівні 2, а мінімальні - на -2. Зазвичай з базовою косинусною кривою точки, відповідні\(0, \frac{\pi}{2}, \pi, \frac{3 \pi}{2}, 2 \pi\) падати вище, на або нижче лінії в наступній послідовності: вище, на, внизу, на, вище. Негативний знак у рівнянні перемикається вище на нижче і знизу з вище. Весь графік відображається поперек\(x\) -осі.
Напишіть рівняння косинуса для кожної з наступних функцій.
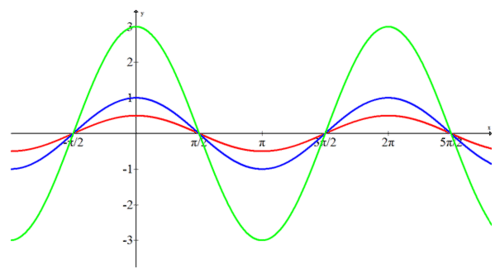
Амплітуди трьох функцій становлять 3,1\(\frac{1}{2}\) і жодна з них не відображається поперек\(x\) осі.
\(f(x)=3 \cdot \cos x\)
\(h(x)=\cos x\)
\(g(x)=\frac{1}{2} \cdot \cos x\)
Зверніть увагу, що сама по собі амплітуда завжди позитивна.
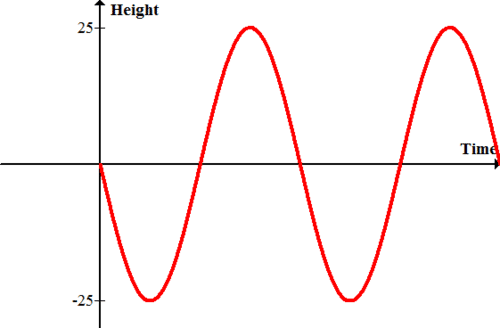
Колесо огляду радіусом 25 футів сидить поруч з платформою. Поїздка починається на платформі і їде вниз, щоб почати. Модель висоти в порівнянні з часом їзди.
Оскільки інформація про час не дається, просто позначте\(x\) вісь як час. За часом нуль висота дорівнює нулю. Спочатку висота буде зменшуватися в міру того, як їзда йде нижче платформи. В кінцевому підсумку колесо знайде мінімум і почне збільшуватися знову до кінця, поки не досягне максимуму.
Знайдіть амплітуду функції\(f(x)=-3 \cos x\) і використовуйте мову перетворень, щоб описати, як графік пов'язаний з батьківською функцією\(y=\cos x\).
Нова функція відбивається поперек\(x\) осі і вертикально розтягується в 3 рази.
Рецензія
1. Поясніть, як знайти амплітуду синусоїдальної функції з її рівняння.
2. Поясніть, як знайти амплітуду синусоїдальної функції з її графіка.
Знайдіть амплітуду кожної з наступних функцій.
3. \(g(x)=-5 \cos x\)
4.
5. \(f(x)=\frac{1}{2} \sin x\)
6.
7. \(j(x)=3.12 \cos x\)
8.
Намалюйте кожну з наступних функцій.
9. \(f(x)=3 \sin x\)
10. \(g(x)=-4 \cos x\)
11. \(h(x)=\pi \sin x\)
12. \(k(x)=-1.2 \cos x\)
13. \(p(x)=\frac{2}{3} \cos x\)
14. \(m(x)=-\frac{1}{2} \sin x\)
15. Попередній перегляд:\(r(x)=3 \sin x+2\)