Skip to main content
LibreTexts - Ukrayinska

5.4: Вертикальний зсув синусоїдальних функцій

  1. Last updated
  2. Save as PDF
  • Page ID
    54647

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ваші знання про перетворення, зокрема вертикальний зсув, стосуються безпосередньо синусоїдальних функцій. На практиці ескізування зсунутих синусоїдних і косинусних функцій вимагає більшої уваги до деталей і більш ретельного маркування, ніж інші функції. Чи можете ви описати наступну трансформацію словами?

    \(f(x)=\sin x \rightarrow g(x)=-3 \sin x-4\)

    В якому порядку відбуваються відображення, розтягування і зсув? Чи є різниця?

    Вертикальний зсув синусоїдальних функцій

    Загальна форма синусоїдальної функції - це:

    \(f(x)=\pm a \cdot \sin (b(x+c))+d\)

    Нагадаємо, що\(a\) контролює амплітуду і\(\pm\) контролює відображення. Тут ви побачите, як\(d\) управляє вертикальним зсувом.

    Найбільш простий спосіб подумати про вертикальний зсув синусоїдальних функцій - зосередитися на синусоїдальній осі, горизонтальній лінії, що проходить через середину синусоїдальної або косинусоїдальної хвилі. На початку завдання виявляють вертикальний зсув і відразу ж малюють нову синусоїдальну вісь. Потім перейдіть до амплітуди графіка та відображення навколо цієї осі на відміну від\(x\) осі.

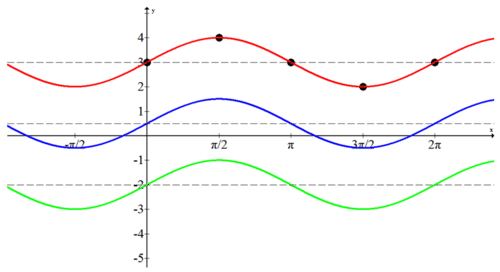
    Графіки наступних трьох функцій наведені нижче:

    \(f(x)=\sin x+3\)
    \(g(x)=\sin x-2\)
    \(h(x)=\sin x+\frac{1}{2}\)

    Щоб намалювати ці графіки, спочатку малюється нова синусоїдальна вісь для кожного графіка. Потім малюється повна синусоїда для кожної з них. Зверніть увагу на п'ять важливих моментів, які розділяють кожен квадрант, щоб допомогти отримати чітке уявлення про графік. У цих графіках немає відображень, і всі вони мають амплітуду 1. Зараз кожен цикл починається з 0 і закінчується на,\(2 \pi\) але це не завжди буде так.

    Перегляньте частини наступного відео, зосередженого на вертикальних перекладах:

    Приклади

    Приклад 1

    Раніше вас запитали, в якому порядку вертикальний зсув і відображення слід виконувати і якщо це має значення. Наступне перетворення можна описати наступним чином.

    \(f(x)=\sin x \rightarrow g(x)=-3 \sin x-4\)

    Опишіть спочатку розтягування і відображення, а потім вертикальний зсув. Це найбільш логічний спосіб обговорення перетворення усно, оскільки тоді числа, такі як 3 та -4, можуть бути явно визначені на графіку.

    Порядок в описі трансформації має значення. При описі вертикальних перетворень найбільш інтуїтивно просто описати перетворення в тому ж порядку, що і порядок операцій.

    Приклад 2

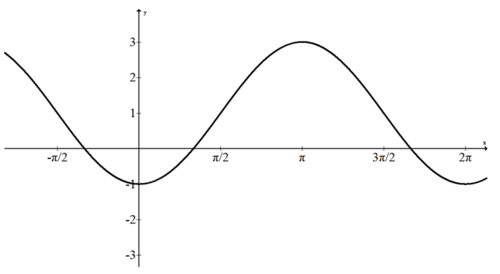
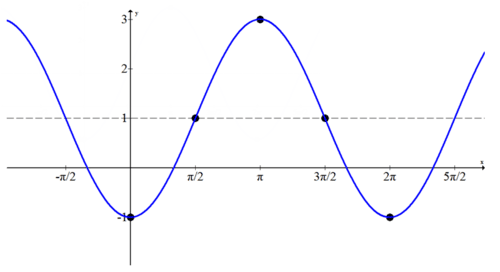
    Визначте рівняння наступного перетвореного косинусного графа.

    оскільки відсутня синусоїдальна вісь, необхідно визначити вертикальний зсув, розтягнення і відображення. Пік відбувається в\((\pi, 3)\) і жолоб відбувається на (0, -1), тому горизонтальна лінія безпосередньо між +3 і -1\(y=1\) є. оскільки синусоїдальна вісь була зрушена вгору на одну одиницю\(d=1\). З цієї висоти графік йде два вище і два нижче, що означає, що амплітуда дорівнює 2. Оскільки цей косинусний графік починає свій цикл з (0, -1), який є нижчою точкою, це негативний косинус. Функція є\(f(x)=-2 \cos x+1\)

    Приклад 3

    Перетворіть наступний синусовий графік двома способами. Спочатку перетворіть синусоїдальний графік, змістивши його вертикально вгору на 1 одиницю, а потім розтягнувши його по вертикалі в 2 одиниці. По-друге, перетворіть синусоїдальний графік, розтягнувши його по вертикалі в 2 одиниці, а потім змістивши його вертикально вгору на 1 одиницю.

    Роблячи впорядковані перетворення, добре показати, з чого ви починаєте і де в кінцевому підсумку, щоб ви могли ефективно порівнювати та протиставити результати. Подивіться, як обидва перетворення починаються із звичайної синусоїди. Два стовпці представляють послідовність перетворень, які дають різні результати.

    Приклад 4

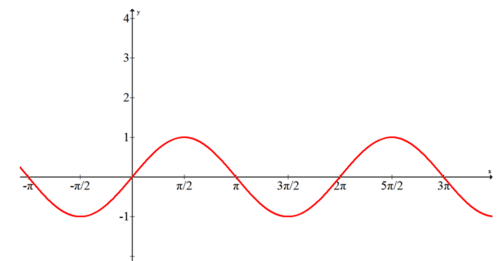
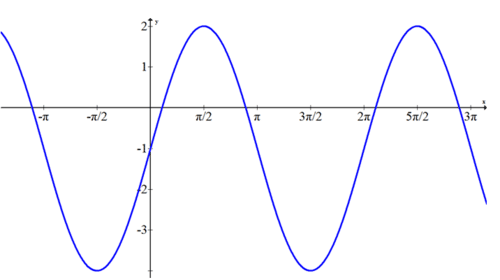
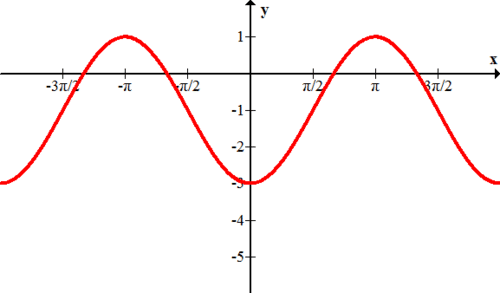
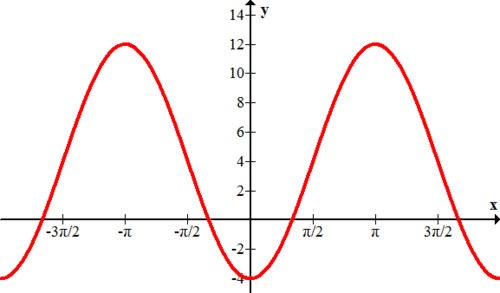
    Яке рівняння моделює наступний графік?

    \(f(x)=3 \cdot \sin x-1\)

    Приклад 5

    Графік наступної функції:\(f(x)=-2 \cdot \cos x+1\)

    Спочатку намалюйте горизонтальну синусоїдальну вісь і виділіть п'ять основних точок для косинусоїдальної хвилі. Будьте обережні, щоб відзначити, що амплітуда дорівнює 2, а косинусна хвиля починається і закінчується в низькій точці через негативний знак.

    Рецензія

    Графік кожної з наступних функцій, які зазнали вертикального розтягування, відображення та/або вертикального зсуву.

    1. \(f(x)=-2 \sin x+4\)

    2. \(g(x)=\frac{1}{2} \cos x-1\)

    3. \(h(x)=3 \sin x+2\)

    4. \(j(x)=-1.5 \cos x+\frac{1}{2}\)

    5. \(k(x)=\frac{2}{3} \sin x-3\)

    Знайдіть мінімальне і максимальне значення кожної з наступних функцій.

    6. \(f(x)=-3 \sin x+1\)

    7. \(g(x)=2 \cos x-4\)

    8. \(h(x)=\frac{1}{2} \sin x+1\)

    9. \(j(x)=-\cos x+5\)

    10. \(k(x)=\sin (x)-1\)

    Дайте рівняння кожної функції на графіку нижче.

    11.

    12.

    13.

    14.

    15.