2.9 Вертикальні асимптоти

Базовою раціональною функцією$f(x)=\frac{1}{x}$ є гіпербола з вертикальною асимптотою при$x=0$. Більш складні раціональні функції можуть мати множинні вертикальні асимптоти. Ці асимптоти є дуже важливими характеристиками функції так само, як дірки. Обидві дірки і вертикальні асимптоти виникають при$x$ значеннях, які роблять знаменник функції нулем. Водійське питання: чим вертикальні асимптоти відрізняються від отворів?

Пошук вертикальних асимптотів

Вертикальні асимптоти виникають, коли множник знаменника раціонального виразу не скасовується з множником від чисельника. Якщо у вас є коефіцієнт, який не скасовує, замість того, щоб зробити отвір у цьому$x$ значенні, існує вертикальна асимптота. Вертикальна асимптота представлена пунктирною вертикальною лінією. Більшість калькуляторів не ідентифікують вертикальні асимптоти, а деякі неправильно намалюють круту лінію як частину функції, де насправді існує асимптота.

Ваша робота полягає в тому, щоб мати можливість ідентифікувати вертикальні асимптоти з функції та описати кожну асимптоту за допомогою рівняння вертикальної лінії.

Візьміть наступну раціональну функцію:

$f(x)=\frac{(2 x-3)(x+1)(x-2)}{(x+2)(x+1)}$

Щоб визначити дірки та рівняння вертикальних асимптотів, спочатку вирішіть, які фактори скасовують. Фактор, який скасовує, являє собою знімний розрив. Є отвір при (-1,15). Вертикальна асимптота виникає при$x=-2$ тому, що фактор$x+2$ не скасовується.

Подивіться наступне відео, зосередившись на частинами про вертикальні асимптоти.

Приклад 1

Раніше вас запитали, чим асимптоти відрізняються від дірок. Дірки виникають при скасуванні множників з чисельника і знаменника. Коли коефіцієнт у знаменнику не скасовується, він створює вертикальну асимптоту. І дірки, і вертикальні асимптоти обмежують область раціональної функції.

Приклад 2

Напишіть функцію, яка відповідає наступним критеріям:

• Вертикальні асимптоти при 0 і 3
• Нулі на 2 і 5
• Отвір на (4, 2)

Кожен критерій допомагає побудувати функцію. Вертикальні асимптоти мають на увазі, що знаменник має два фактори, які не скасовуються чисельником:

$\frac{1}{x \cdot(x-3)}$

Нулі в 2 і 5 означають, що чисельник має два фактори, які не скасовують.

$\frac{(x-2)(x-5)}{x \cdot(x-3)}$

Отвір в (4,2) означає, що існує коефіцієнт$x-4$, який скасовує чисельник і знаменник.

$\frac{(x-2)(x-5)(x-4)}{x \cdot(x-3)(x-4)}$

Складна частина полягає в тому, що висота функції повинна бути 2 після скасування$x-4$ множника і 4 підставляється в. В даний час це$-\frac{1}{2}$

$\frac{(4-2)(4-5)}{4 \cdot(4-3)}=-\frac{1}{2}$

Для того щоб отвір існувало на висоті 2, потрібно помножити функцію на скаляр -4.

$f(x)=\frac{-4(x-2)(x-5)(x-4)}{x \cdot(x-3)(x-4)}$

Приклад 3

Намалюйте вертикальні асимптоти для наступної функції.

$f(x)=\frac{1}{(x-4)(x-2)(x+3)}$

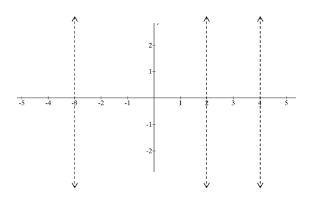
Зверніть увагу, що ви можете не знати характеристик того, що функція робить всередині цих вертикальних ліній. Незабаром ви дізнаєтеся, як використовувати тести знаків, а також методи, які ви вже навчилися заповнювати чотири розділи, на які поділена ця функція.

Приклад 4

Визначте дірки та рівняння вертикальних асимптотів наступної раціональної функції.

$f(x)=\frac{3(x-1)(x+2)(x-3)(x+4)}{5\left(x+\frac{1}{2}\right)(2+x)(3-x)(x-8)}$

Вертикальні асимптоти виникають при$x=-\frac{1}{2}, x=8 .$ Отвори виникають, коли$x$ дорівнює -2 і$3 .$ Щоб отримати висоту отворів у цих точках, не забудьте скасувати те, що можна скасувати, а потім підставити значення. Дуже поширена помилка - забути скасувати$\frac{x-3}{3-x}=-1$

$\begin{aligned} g(x) &=\frac{-3(x-1)(x+4)}{5\left(x+\frac{1}{2}\right)(x-8)} \\ g(-2) &=\frac{6}{25} \\ g(3) &=\frac{12}{25} \end{aligned}$

Отвори знаходяться на$\left(-2, \frac{6}{25}\right),\left(3, \frac{12}{25}\right)$

Приклад 5

Визначте область наступної функції, а потім визначте дірки та вертикальні асимптоти.

$f(x)=\frac{(3 x-4)(1-x)\left(x^{2}+4\right)}{(3 x-2)(x-1)}$

Домен функції, записаної в інтервальному позначенні:$\left(-\infty, \frac{2}{3}\right) \cup\left(\frac{2}{3}, 1\right) \cup(1, \infty) .$ Зверніть увагу, що домен - це всі дійсні числа, за винятком тих випадків, коли знаменник дорівнює нулю.

Розрізняють дві розриви: одна - дірка, а друга - вертикальна асимптота. Отвір виникає при (1,5) Вертикальна асимптота виникає при$x=\frac{2}{3}$

Зверніть увагу, що дірки ідентифікуються як точки, тоді як вертикальні асимптоти ідентифікуються як лінії форми,
$x=a$ де$a$ є певна константа.

Рецензія

1. Напишіть функцію, яка відповідає наступним критеріям:

• Вертикальні асимптоти в 1 і 4
• Нулі на 3 і 5
• Отвір в (6, 3)

2. Напишіть функцію, яка відповідає наступним критеріям:

• Вертикальні асимптоти при -2 і 2
• Нулі на 1 і 5
• Отвір при (3, -4)

3. Напишіть функцію, яка відповідає наступним критеріям:

• Вертикальні асимптоти при 0 і 3
• Нулі на 1 і 2
• Отвір в (8, 21)

4. Напишіть функцію, яка відповідає наступним критеріям:

• Вертикальні асимптоти на 2 і 6
• Нуль на 5
• Отвір на (4, 1)

5. Напишіть функцію, яка відповідає наступним критеріям:

• Вертикальна асимптота при 4
• Нулі при 0 і 3
• Отвір в (5, 10)

Дайте рівняння вертикальних асимптотів для наступних функцій.

6. $f(x)=\frac{(2-x)}{(x-2)(x-4)}$

7. $g(x)=\frac{-x}{(x+1)(x-3)}$

8. $h(x)=6-\frac{x+2}{(x+1)(x-5)}$

9. $j(x)=\frac{10}{x-3}-\frac{x}{(x+2)(x-3)}$

10. $k(x)=2-\frac{(4-x)}{(x+3)(x-4)}$

Визначте дірки та рівняння вертикальних асимптотів наступних раціональних функцій.

11. $f(x)=\frac{3(x-1)(x+1)(x-4)(x+4)}{4(x+4)(2+x)(4-x)(x+1)}$

12. $g(x)=\frac{x(x-3)(x-8)(x-3)(x+4)}{7(x+1)(1+x)(3-x)(x-8)}$

Створіть область наступних раціональних функцій.

13. $h(x)=\frac{x(x+1)(x-3)(x+4)}{x(3-x)(x-1)}$

14. $j(x)=\frac{x^{2}+3 x-4}{x^{2}-6 x-16}$

15. $k(x)=\frac{2 x-10}{x^{3}+4 x^{2}+3 x}$