2.10 Горизонтальні асимптоти

Last updated

Oct 27, 2022
Save as PDF
- 2.6: Рішення раціональних рівнянь
- 2.11 Косий асимптот

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Вертикальні асимптоти описують поведінку функції як значення $x$ наближення до певного числа. Горизонтальні асимптоти описують поведінку функції як значення $x$ стають нескінченно великими і нескінченно малими. оскільки функції не можуть торкатися вертикальних асимптотів, чи не дозволяється їм торкатися і горизонтальних асимптотів?

Знаходження горизонтальних асимптотів

Горизонтальні асимптоти є засобом опису кінцевої поведінки функції. Поведінка кінця по суті є описом того, що відбувається по обидва боки графіка, оскільки функція продовжується вправо і вліво нескінченно. При визначенні горизонтальних асимптотів важливо враховувати і праву, і ліву сторони, тому що горизонтальні асимптоти не обов'язково будуть однаковими в обох місцях. Розглянемо зворотну функцію і зверніть увагу, як як $x$ йде вправо і вліво вона згладжується до лінії $y=0$ .

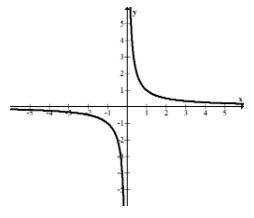
Іноді функції згладжуються, а в інших випадках функції збільшуються або зменшуються без обмежень. Є в основному три випадки.

Випадок 1: Ступінь чисельника менше ступеня знаменника

Перший випадок полягає в тому, що функція згладжується до 0, оскільки $x$ стає нескінченно великою або нескінченно маленькою. Це відбувається, коли ступінь чисельника менше ступеня знаменника. Ступінь визначається найбільшим показником $x$ .

$f(x)=\frac{2 x^{8}+3 x^{2}+100}{x^{9}-12}$

Один із способів пояснити, чому це має сенс, $x$ полягає в тому, що коли це смішно велика кількість, то більшість частин функції навряд чи впливають. Наприклад, 100 - це ніщо в порівнянні, і ні $3 x^{2}$ . Два важливі терміни для порівняння - це $x^{8}$ і $x^{9}$ . 2 зараз навіть не важливо, тому що якщо $x$ навіть мільйон, ніж $x^{9}$ буде в мільйон разів більше, ніж $x^{8}$ і 2 навряд чи має значення знову. По суті, коли $x$ стає досить великим, ця функція діє як $\frac{1}{x}$ яка має горизонтальну асимптоту $0 .$

Випадок 2: Ступінь чисельника дорівнює ступені знаменника

Якщо ступінь чисельника дорівнює ступеня знаменника, то горизонтальна асимптота дорівнює відношенню провідних коефіцієнтів.

$f(x)=\frac{6 x^{4}-3 x^{3}+12 x^{2}-9}{3 x^{4}+144 x-0.001}$

Зверніть увагу, як ступінь чисельника і знаменника дорівнює 4. Це означає, що горизонтальна асимптота є $y=\frac{6}{3}=2$ . Один із способів пояснити, чому це має сенс, полягає в тому, що коли $x$ стає дуже великою кількістю, всі менші повноваження насправді не зроблять значного впливу. Найбільші учасники — це лише найбільші повноваження. Тоді значення чисельника буде приблизно в два рази більше, ніж у знаменника. Як $x$ стає ще більше, то функція стане ще ближче до 2.

Випадок 3: Ступінь чисельника більше, ніж ступінь знаменника

Якщо ступінь чисельника більше ступеня знаменника, горизонтальної асимптоти не існує. Ви повинні визначити, чи збільшується або зменшується функція без обмежень як в лівому, так і в правому напрямку.

Подивіться наступне відео, зосередившись на ділянках про горизонтальні асимптоти.

Приклади

Приклад 1

Раніше вас запитали, чи дозволено функціям торкатися їх горизонтальних асимптотів. Функції можуть торкатися і проходити через горизонтальні асимптоти без обмежень. Це різниця між вертикальними і горизонтальними асимптотами. У обчисленні є суворі докази, які показують, що функції, подібні до того, що в прикладі C, стають довільно близькими до асимптоти.

Приклад 2

Визначте вертикальні і горизонтальні асимптоти наступної раціональної функції.

$f(x)=\frac{(x-2)(4 x+3)(x-4)}{(x-1)(4 x+3)(x-6)}$

Існує фактор, який скасовує, який не є ні горизонтальною, ні вертикальною асимптотою. Вертикальні асимптоти виникають при $x=1$ і $x=6$ . Щоб отримати горизонтальну асимптоту, ви можете методично помножити кожен біном, однак оскільки більшість цих членів не мають значення, ефективніше спочатку визначити відносні сили чисельника та знаменника. У цьому випадку вони обидва трапляються 3. Далі визначаємо коефіцієнт тільки кубічних домішок. Чисельник буде мати $4 x^{3}$ і знаменник буде мати, $4 x^{3}$ і тому горизонтальна асимптота буде відбуватися при $y=\frac{4}{4}=1$

Приклад 3

Опишіть поведінку правого кінця наступної функції.

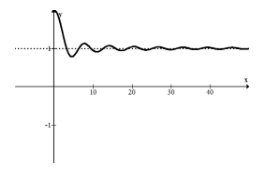
Зверніть увагу, як швидко ця функція гасіння хвилі осідає. Здається, є очевидна горизонтальна вісь праворуч $y=1$

Приклад 4

Визначте горизонтальні асимптоти наступної функції.

$f(x)=\frac{(x-3)(x+2)}{|(x-5)| \cdot(x-1)}$

Спочатку зверніть увагу на абсолютне значення, що оточує один із термінів у знаменнику. Ступені як чисельника, так і знаменника будуть 2, що означає, що горизонтальна асимптота буде відбуватися за числом. Як $x$ стає нескінченно великим, функція приблизно:

$f(x)=\frac{x^{2}}{x^{2}}$

Таким чином, горизонтальна асимптота $y=-1$ як $x$ стає нескінченно великий.

З іншого боку, як $x$ стає нескінченно мало, функція приблизно:

$f(x)=\frac{x^{2}}{-x^{2}}$

Таким чином, горизонтальна асимптота $y=-1$ як $x$ стає нескінченно малий.

У цьому випадку ви не можете сліпо використовувати правило провідного коефіцієнта, оскільки абсолютне значення змінює знак.

Приклад 5

Визначте горизонтальні асимптоти, якщо вони існують для наступних 3 функцій.

1. $f(x)=\frac{3 x^{6}-72 x}{x^{6}+999}$

Ступені чисельника і знаменника рівні так горизонтальна асимптота $y=3$ .

2. $h(x)=\frac{a x^{4}+b x^{3}+c x^{2}+d x+e}{f x^{4}+g x^{3}+h x^{2}}$

Ступені чисельника і знаменника знову рівні, тому горизонтальна асимптота дорівнює $y=\frac{a}{f}$

3. $g(x)=\frac{f(x)}{h(x)}$

Як $x$ стає нескінченно великий,

$g(x)=\frac{f(x)}{h(x)}=\frac{\frac{3 x^{6}-72 x}{x^{6}+999}}{\frac{a x^{4}+b x^{3}+c x^{2}+d x+e}{f x^{4}+g x^{3}+h x^{2}}} \approx \frac{3}{\frac{a}{f}}=\frac{3 f}{a}$

Коли ви вивчаєте обчислення, ви дізнаєтеся суворі методи, які дозволяють вам відчувати себе більш впевнено щодо таких результатів.

Рецензія

Визначте горизонтальні асимптоти, якщо вони існують, для наступних функцій.

1. $f(x)=\frac{5 x^{4}-2 x}{x^{4}+32}$

2. $g(x)=\frac{3 x^{4}-2 x^{6}}{-x^{4}+2}$

3. $h(x)=\frac{3 x^{4}-5 x}{8 x^{3}+3 x^{4}}$

4. $j(x)=\frac{2 x^{3}-15 x}{-x^{4}+3}$

5. $k(x)=\frac{2 x^{5}-3 x}{5 x^{2}+3 x^{4}+2 x-7 x^{5}}$

6. $f(x)=\frac{a x^{14}+b x^{23}+c x^{12}+d x+e}{f x^{24}+g x^{23}+h x^{21}}$

7. $g(x)=\frac{(x-1)(x+4)}{|(x-2)| \cdot(x-1)}$

8. Напишіть функцію, яка відповідає наступним критеріям:

Вертикальні асимптоти при $x=1$ і $x=4$
Нулі на 3 і 5
Отвір при $x=6$
Горизонтальна асимптота при $y=\frac{2}{3}$

9. Напишіть функцію, яка відповідає наступним критеріям:

Вертикальні асимптоти при $x=-2$ і $x=2$
Нулі на 1 і 5
Отвір при $x=3$
Горизонтальна асимптота при $y=1$

10. Напишіть функцію, яка відповідає наступним критеріям:

Вертикальні асимптоти при $x=0$ і $x=3$
Нулі на 1 і 2
Отвір при $x=8$
Горизонтальна асимптота при $y=2$

11. Напишіть функцію, яка відповідає наступним критеріям:

Вертикальні асимптоти на 2 і 6
Нуль на 5
Отвір при $x=4$
Горизонтальна асимптота при $y=0$

12. Напишіть функцію, яка відповідає наступним критеріям:

Вертикальна асимптота при 4
Нулі при 0 і 3
Отвір при $x=5$
Немає горизонтальних асимптотів

Визначте вертикальні та горизонтальні асимптоти наступних раціональних функцій.

13. $f(x)=\frac{(x-5)(2 x+1)(x-3)}{(x-3)(4 x+5)(x-6)}$

14. $g(x)=\frac{x(x-1)(x+3)(x-5)}{3 x(x-1)(4 x+3)}$

15. $h(x)=\frac{(x-2)(x+3)(x-6)}{(x-4)(x+3)^{2}(x+2)}$