2.11 Косий асимптот
- Page ID
- 54517
Коли ступінь чисельника раціональної функції перевищує ступінь знаменника на одиницю, то функція має косі асимптоти. Для того, щоб знайти ці асимптоти, потрібно використовувати поліноміальне довге ділення і незалишкова частина функції стає косою асимптотою. Задати природне запитання: що відбувається, коли ступінь чисельника перевищує ступінь знаменника більш ніж на одиницю?
Косий асимптот
Наступна функція показана до і після виконання поліноміального довгого ділення.
\(f(x)=\frac{x^{4}+3 x^{2}+2 x+14}{x^{3}-3 x^{2}}=x+3+\frac{12 x^{2}+2 x+14}{x^{3}-3 x^{2}}\)
Зверніть увагу, що частина решти буде йти до нуля, коли\(x\) стає надзвичайно великим або надзвичайно малим, оскільки потужність чисельника менше, ніж сила знаменника. Це означає, що, хоча ця функція може йти haywire з малими абсолютними значеннями\(x\), великі\(x\) абсолютні значення надзвичайно близькі до лінії\(y=x+3\).
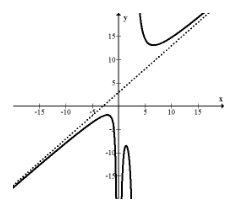
Косими асимптотами є ці похилі асимптоти, які показують, як саме функція збільшується або зменшується без обмежень. Косі асимптоти також називають похилими асимптотами.
Іноді функція матиме асимптоту, яка не схожа на рядок. Погляньте на наступну функцію:
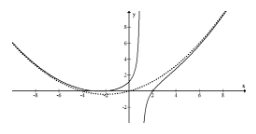
\(f(x)=\frac{\left(x^{2}-4\right)(x+3)}{10(x-1)}\)
Ступінь чисельника дорівнює 3, тоді як ступінь знаменника дорівнює 1, тому похила асимптота не буде лінією. Однак, коли графік спостерігається, все ще існує чітка закономірність щодо того, як ця функція збільшується без обмежень, оскільки\(x\) наближається до дуже великих і дуже малих чисел.
\(f(x)=\frac{1}{10}\left(x^{2}+4 x\right)-\frac{12}{10(x-1)}\)
Як бачите, це виглядає як парабола з залишком. Ця раціональна функція має хребет параболи. Магістраль - це функція, до якої прагне графік. Це технічно не коса асимптота, оскільки це не лінія.
Приклади
Раніше вас запитали, що відбувається, коли сила чисельника перевищує силу знаменника більш ніж на одиницю. Як видно вище, коли сила чисельника перевищує силу знаменника більш ніж на одиницю, функція розвиває кістяк, який має форму будь-якого многочлена. Косі асимптоти - це завжди лінії.
Знайдіть асимптоти та перехоплення функції:
\(f(x)=\frac{x^{3}}{x^{2}-4}\)
Функція має вертикальні асимптоти при\(x=\pm 2\).
Після тривалого поділу функція стає:
\(f(x)=x+\frac{4}{x^{2}-4}\)
Це робить косу асимптоту при\(y=x\)
Визначте вертикальні і косі асимптоти наступної раціональної функції.
\ [
f (x) =\ розрив {x^ {3} -x^ {2} -x-1} {(x-3) (х+4)}
\]
Після використання поліноміального довгого ділення та перезапису функції з часткою залишку та без залишку вона виглядає так:
\ [
f (x) = х-2+\ розрив {13 х-25} {x^ {2} +х-12} =х-2+\ розрив {13 х-25} {(x-3) (х+4)}
\]
Коса асимптота є\(y=x-2\). Вертикальні асимптоти знаходяться в\(x=3\) і\(x=-4\) які легше спостерігати в останній формі функції, оскільки вони явно не скасовуються, щоб стати дірками.
Створіть функцію з косою асимптотою при\(y=3 x-1,\) вертикальних асимптотах при\(x=2,-4\) і включає дірку, де\(x\) дорівнює 7.
Хоча існує нескінченна кількість функцій, які відповідають цим критеріям, один із прикладів:
\ [
f (x) =3 х-1+\ розрив {(x-7)} {(x-2) (х+4) (х-7)}
\]
Визначте кістяк наступної функції і поясніть, чому функція не має косої асимптоти.
\ [
f (x) =\ розриву {5 x^ {5} +27} {x^ {3}}
\]
Хоча багаточлен довгий поділ можливо, також можна просто розділити кожен член на\(x^{3}\).
\ [
f (x) =\ розрив {5 x^ {5} +27} {x^ {3}} =\ розрив {5 x^ {5}} {x^ {3}} +\ розрив {27} {x^ {3}} =5 x^ {2} +\ розрив {27} {x^ {3}}
\]
Опорою цієї функції є парабола\(y=5 x^{2}\). Це не коса асимптота, оскільки це не лінія.
Рецензія
1. Що таке коса асимптота?
2. Як ви можете визначити, дивлячись на рівняння функції, якщо вона буде мати косу асимптоту чи ні?
3. Чи може функція мати як косу асимптоту, так і горизонтальну асимптоту? Поясніть.
Для кожного з наступних графіків намалюйте графік, а потім намалюйте в косому асимптоті, якщо він існує. Якщо його не існує, поясніть, чому б ні.
4.
5.
6.
7.
8.
Знайдіть рівняння косої асимптоти для кожної з наступних раціональних функцій. Якщо косою асимптоти немає, поясніть чому б ні і дайте рівняння хребта функції, якщо така існує.
9. \(f(x)=\frac{x^{3}-7 x-6}{x^{2}-2 x-15}\)
10. \(g(x)=\frac{x^{3}-7 x-6}{x^{4}-3 x^{2}-10}\)
11. \(h(x)=\frac{x^{2}+5 x+6}{x^{2}+2 x+1}\)
12. \(k(x)=\frac{x^{4}+9 x^{3}+21 x^{2}-x-30}{x^{2}+2 x+1}\)
13. Створіть функцію з косими асимптотами при\(y=2 x-1,\) вертикальній асимптоті в\(x=3\) і дірці, де\(x\) дорівнює 7.
14. Створіть функцію з косою асимптотою в\(y=x\), вертикальні асимптоти при\(x=1,-3\) і без дірок.
15. Чи має парабола косий асимптот? А як щодо кубічної функції?




