2.4: Раціональні вирази

Раціональний вираз - це співвідношення, точно так само, як дріб. Однак замість співвідношення між числами раціональним виразом є співвідношення між двома виразами.

Одне з рушійних питань, яке слід задати, полягає в тому, що правила спрощення та дії на раціональних виразах збігаються з правилами спрощення та роботи на дробах?

Робота з раціональними виразами

При спрощенні або роботі над раціональними виразами життєво важливо, щоб кожен поліном був повністю врахований. Після того, як всі вирази будуть враховані, однакові множники в чисельнику та знаменнику можуть бути скасовані або вилучені. Причина, по якій вони можуть бути видалені, полягає в тому, що будь-який вираз, розділений сам по собі, дорівнює 1. Ідентичний вираз в чисельнику і знаменнику - це просто вираз ділиться сам по собі, і так дорівнює 1.

Додавання та віднімання раціональних виразів

Щоб додати або відняти раціональні вирази, важливо спочатку знайти загальний знаменник. У той час як будь-який спільний знаменник буде працювати, використання найменш спільного знаменника - це засіб утримання під контролем кількості додаткових факторів. Подивіться на кожне раціональне вираження, з яким ви працюєте, і визначте бажаний спільний знаменник. Помножте кожен вираз на відповідну форму 1, наприклад\(\frac{x-2}{x-2}\), і тоді ви повинні мати свій спільний знаменник. Крім завдань додавання та віднімання, чисельник повинен бути множений, об'єднаний та повторно врахований, щоб вважати спрощеним.

Множення та ділення раціональних виразів

Щоб помножити раціональні вирази, слід написати добуток всіх чисельників на добуток всіх знаменників множників, а потім скасувати або видалити однакові фактори.Щоб розділити раціональні вирази, слід переписати задачу ділення як задачу множення. Перше раціональне вираз помножте на зворотне другого раціонального виразу. Виконайте наведені вище дії для множення. Як у задачах множення, так і ділення відповіді найчастіше залишаються повністю врахованими, щоб продемонструвати, що все було зменшено належним чином.

Приклади

Приклад 1

Раніше вас запитали, чи збігаються правила спрощення і роботи над раціональними виразами з правилами спрощення і дії на дробах. Раціональні вирази - це розширення дробів і операції спрощення, додавання, віднімання, множення і ділення працюють точно так само.

Приклад 2

Відніміть такі раціональні вирази.

\(\frac{x-2}{x+3}-\frac{x^{3}-3 x^{2}+8 x-24}{2(x+2)\left(x^{2}-9\right)}\)

Вміння ефективно впливати має першорядне значення.

\(=\frac{x-2}{x+3}-\frac{x^{3}-3 x^{2}+8 x-24}{2(x+2)\left(x^{2}-9\right)}\)
\(=\frac{(x-2)}{(x+3)}-\frac{x^{2}(x-3)+8(x-3)}{2(x+2)\left(x^{2}-9\right)}\)
\(=\frac{(x-2)}{(x+3)}-\frac{(x-3)\left(x^{2}+8\right)}{2(x+2)(x+3)(x-3)}\)

Перш ніж віднімати, спростіть, де це можливо, щоб не сприяти надмірно складним знаменникам.

\(=\frac{(x-2)}{(x+3)}-\frac{x^{2}+8}{2(x+2)(x+3)}\)

Лівого виразу не вистачає\(2(x+2)\), тому помножте і його чисельник, і знаменник на\(2(x+2)\)

\(=\frac{2(x+2)(x-2)}{2(x+2)(x+3)}-\frac{\left(x^{2}+8\right)}{2(x+2)(x+3)}\)
\(=\frac{2\left(x^{2}-4\right)-x^{2}-8}{2(x+2)(x+3)}\)
\(=\frac{x^{2}-16}{2(x+2)(x+3)}\)

Приклад 3

Спростіть наступне раціональне вираз.

\(\frac{x^{2}+7 x+12}{x^{2}+4 x+3} \cdot \frac{x^{2}+9 x+8}{2 x^{2}-128} \div \frac{x+4}{x-8} \cdot \frac{14}{1}\)

Першим фактором все. По-друге, перетворити ділення на множення (всього один член). По-третє, скасуйте відповідним чином, який залишить відповідь.

\(=\frac{(x+3)(x+4)}{(x+3)(x+1)} \cdot \frac{(x+8)(x+1)}{2(x+8)(x-8)} \cdot \frac{(x-8)}{(x+4)} \cdot \frac{14}{1}\)
\(=\frac{(x+3)(x+4)}{(x+3)(x+1)} \cdot \frac{(x+8)(x+1)}{2(x+8)(x-8)} \cdot \frac{(x-8)}{(x+4)} \cdot \frac{14}{1}\)
\(=\frac{14}{2}\)
\(=7\)

У цьому прикладі показано страйк наскрізу. Ви повинні використовувати цю техніку, щоб зіставити коефіцієнти в чисельнику і знаменнику при спрощенні.

Приклад 4

Поєднуйте наступні раціональні вирази.

\(\frac{1}{x^{2}+5 x+6}-\frac{1}{x^{2}-4}+\frac{(x-7)(x+5)+5}{(x+2)(x-2)(x+3)(x-4)}\)

Першим фактором все і визначитися з загальним знаменником. Хоча чисельники насправді не потрібно враховувати, іноді це корисно для спрощення окремих виразів перед їх об'єднанням. Зверніть увагу, що чисельник виразу на правій руці здається факторним, але насправді це не так. Оскільки 5 не пов'язана з рештою чисельника шляхом множення, цю частину виразу потрібно помножити і подібні терміни потрібно об'єднати.

\(=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+2)(x-2)}+\frac{x^{2}-2 x-35+5}{(x+2)(x-2)(x+3)(x-4)}\)
\(=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+2)(x-2)}+\frac{x^{2}-2 x-30}{(x+2)(x-2)(x+3)(x-4)}\)

Зауважте, що правий вираз має 4 фактори в знаменнику, тоді як кожен з лівих виразів має два, які збігаються і два, які відсутні в цих чотирьох факторах. Це говорить вам, на що потрібно помножити кожен вираз, щоб знаменники збігалися.

\(=\frac{(x-2)(x-4)}{(x+2)(x-2)(x+3)(x-4)}-\frac{(x+3)(x-4)}{(x+2)(x-2)(x+3)(x-4)}+\frac{x^{2}-2 x-30}{(x+2)(x-2)(x+3)(x-4)}\)

Тепер, оскільки раціональні вирази мають спільний знаменник, чисельники можна перемножити і об'єднати. Іноді замість повторного переписування виразу в математиці можна використовувати абревіатуру. В цьому випадку можна замінити знаменник буквою\(D\) і потім замінити його в кінці.

\(=\frac{(x-2)(x-4)-(x+3)(x-4)+x^{2}-2 x-30}{D}\)
\(=\frac{x^{2}-6 x+8-\left[x^{2}-x-12\right]+x^{2}-2 x-30}{D}\)

Зверніть увагу, як вкрай важливо використовувати дужки, щоб вказати, що віднімання застосовується до всіх термінів середнього виразу не просто\(x^{2}\). Це одна з найпоширеніших помилок.

\(=\frac{x^{2}-6 x+8-x^{2}+x+12+x^{2}-2 x-30}{D}\)
\(=\frac{x^{2}-7 x-10}{D}\)

Після того, як чисельник був повністю спрощений, спробуйте перерахувати вираз, що залишився і подивитися, якщо щось скасовує з знаменником, який вам тепер потрібно замінити.

\(=\frac{(x+2)(x-5)}{(x+2)(x-2)(x+3)(x-4)}\)
\(=\frac{(x-5)}{(x-2)(x+3)(x-4)}\)

Приклад 5

Спростіть наступний вираз.

\(\frac{\frac{1}{x+1}-\frac{1}{x+2}}{\frac{1}{x-2}-\frac{1}{x+1}}\)

Сам вираз не схоже на раціональний вираз, але його можна переписати, щоб воно було більш впізнаваним. Також важливим навиком є робота з фракціями всередині дробів.

\(=\left(\frac{1}{x+1}-\frac{1}{x+2}\right) \div\left(\frac{1}{x-2}-\frac{1}{x+1}\right)\)
\(=\left[\frac{(x+2)}{(x+1)(x+2)}-\frac{(x+1)}{(x+1)(x+2)}\right] \div\left[\frac{(x+1)}{(x+1)(x-2)}-\frac{(x-2)}{(x+1)(x-2)}\right]\)
\(=\left[\frac{1}{(x+1)(x+2)}\right] \div\left[\frac{3}{(x+1)(x-2)}\right]\)
\(=\frac{1}{(x+1)(x+2)} \cdot \frac{(x+1)(x-2)}{3}\)
\(=\frac{(x-2)}{3(x+2)}\)

Приклад бонусу

Спростіть наступний вираз, який має нескінченну кількість дробів, вкладених в інші дроби.

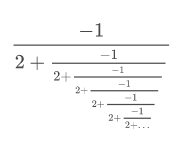
Було б вправою марно намагатися безпосередньо обчислити цей вираз. Замість цього зверніть увагу, що повторюваний характер виразу піддається надзвичайно приємній заміні.

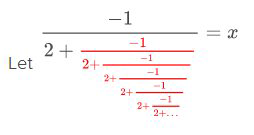
Зверніть увагу, що червона частина дробу точно така ж, як і решта дробу, і тому\(x\) може бути замінена там і вирішена.

\(\begin{aligned} \frac{-1}{2+x} &=x \\-1 &=x(2+x) \\-1 &=x^{2}+2 x \\ 0 &=x^{2}+2 x+1 \\ 0 &=(x+1)^{2} \\ x &=-1 \end{aligned}\)

Причина, чому цей вираз включений в цю концепцію, полягає в тому, що він виділяє один аспект вирішення проблем спрощення виразів, який відрізняє Precalculus від Алгебри 1 та Алгебри 2.

Рецензія

Виконайте зазначену операцію і максимально спростіть.

1. \(\frac{x^{2}+5 x+4}{x^{2}+4 x+3} \cdot \frac{5 x^{2}+15 x}{x+4}\)

2. \(\frac{x^{2}-4}{x^{2}+4 x+4} \cdot \frac{7}{x-2}\)

3. \(\frac{4 x^{2}-12 x}{5 x+10} \cdot \frac{x+2}{x} \div \frac{x-3}{1}\)

4. \(\frac{4 x^{3}-4 x}{x} \div \frac{2 x-2}{x-4}\)

5. \(\frac{2 x^{3}+8 x}{x+1} \div \frac{x}{2 x^{2}-2}\)

6. \(\frac{3 x-1}{x^{2}+2 x-15}-\frac{2}{x+5}\)

7. \(\frac{x^{2}-8 x+7}{x^{2}-4 x-21} \cdot \frac{x^{2}-9}{1-x^{2}}\)

8. \(\frac{2}{x+7}+\frac{1}{x-7}\)

9. \(\frac{6}{x-7}-\frac{6}{x+7}\)

10. \(\frac{3 x+35}{x^{2}-25}+\frac{2}{x+5}\)

11. \(\frac{2 x+20}{x^{2}-4 x-12}+\frac{2}{x+2}\)

12. \(\frac{2}{x+6}-\frac{x-9}{x^{2}-3 x-18}\)

13. \(-\frac{5 x+30}{x^{2}+11 x+30}+\frac{2}{x+5}\)

14. \(\frac{x+3}{x+2}+\frac{x^{3}+4 x^{2}+5 x+20}{2 x^{4}+2 x^{2}-40}\)

15. \(\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\cdots}}}}}}\)