Skip to main content
LibreTexts - Ukrayinska

9.25: Площа поверхні та об'єм сфер

  1. Last updated
  2. Save as PDF
  • Page ID
    54430

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Виведіть і використовуйте формулу: об'єм дорівнює pi,\(\dfrac{4}{3}\) кращому радіусу в кубі.

    Сфери

    Розглянемо суцільну фігуру, що складається з безлічі всіх точок в тривимірному просторі, які знаходяться на рівновіддаленому від однієї точки. Як ви могли визначити, скільки двовимірного та тривимірного простору займає ця фігура?

    Сфера - це сукупність всіх точок в тривимірному просторі, які знаходяться на рівній відстані від однієї точки. Радіус сфери має одну кінцеву точку на поверхні сфери, а іншу кінцеву точку в центрі цієї сфери. Діаметр сфери повинен містити центр.

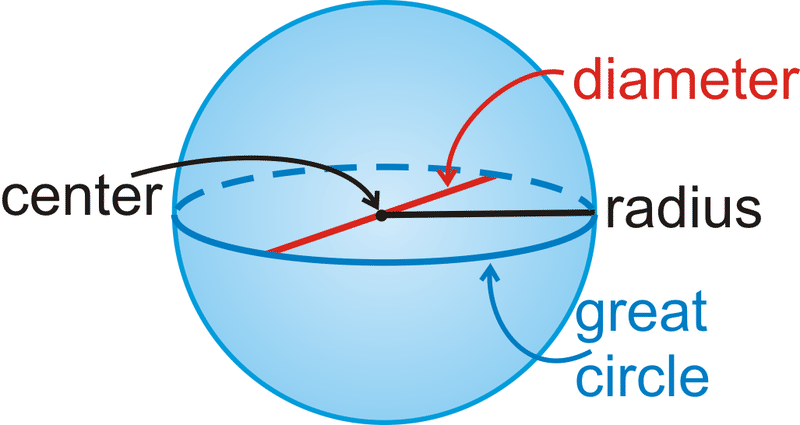
    F-д_д6901д 55б629c386c0641d1a93b432f521a443f41b631A635b57C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Велике коло є найбільшим круглим перетином у сфері. Окружність сфери - це окружність великого кола. Кожне велике коло ділить сферу на дві конгруентні півкулі .

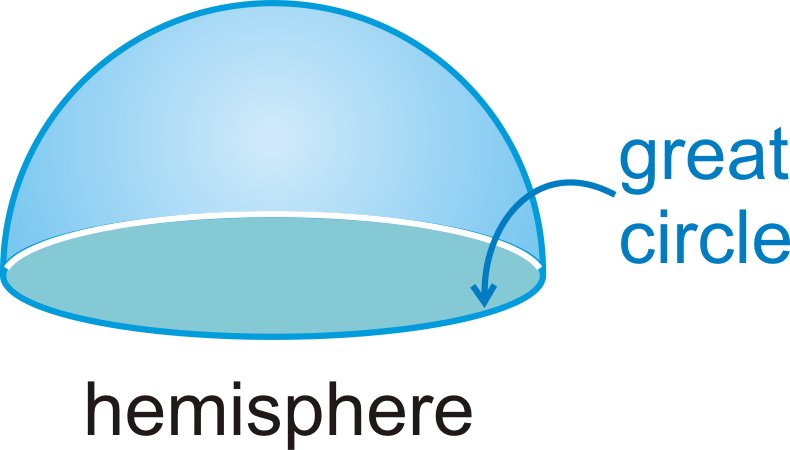
    F-д_Е8Е 831771893961 AE1E76F94C46 ДБ5С08А8ДБ8Д 5804Ф710Де4ДФ 93+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Площа поверхні

    Площа поверхні - це двовимірне вимірювання, яке є загальною площею всіх поверхонь, які зв'язали тверде тіло. Основною одиницею площі є квадратна одиниця.

    Площа поверхні сфери:\(SA=4\pi r^{2}\)

    F-D_0DC BEF 245Б10Б2260Б202А695Б3958 ФДБ 04CD19C27C9EB245876CD6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Обсяг

    Щоб знайти обсяг будь-якого твердого тіла, ви повинні з'ясувати, скільки місця воно займає. Основною одиницею об'єму є кубічна одиниця.

    Обсяг сфери:\(V=\dfrac{4}{3}\pi r^{3}\)

    F-D_0DC BEF 245Б10Б2260Б202А695Б3958 ФДБ 04CD19C27C9EB245876CD6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Приклад\(\PageIndex{1}\)

    Знайдіть площу поверхні малюнка нижче, півсфери з круговим підставою.

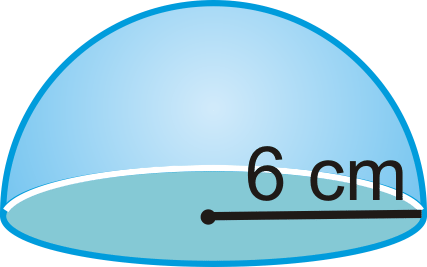
    Ф-д_1С8А850Ф4Б14Б8Е2Д4С602187936454А1578БА 198D1ФЕД 823EBD9A20+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Скористайтеся формулою для площі поверхні:

    \(\begin{aligned} SA&=\pi r^{2} +124\pi r^{2} \\ &=\pi (6^{2})+2\pi (6^{2}) \\&=36\pi +72\pi =108\pi \text{ cm}^{2}\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Куля має об'єм 14 137.167 ft3. Що таке радіус?

    Рішення

    Скористайтеся формулою для обсягу, підключіть заданий обсяг і вирішіть для радіуса, r:

    \(\begin{aligned} V&=\dfrac{4}{3}\pi r^{3} \\ 14,137.167&=\dfrac{4}{3}\pi r^{3} \\ \dfrac{3}{4\pi} \cdot 14,137.167&=r^{3} \\ 3375&\approx r^{3}\end{aligned}\)

    У цей момент вам потрібно буде взяти кубоподібний корінь 3375. У вашому калькуляторі може бути кнопка, яка виглядає як\ sqrt [3] {}, або ви можете скористатися\(3375^{\dfrac{1}{3}}\).

    \(\sqrt[3]{3375}=15\approx r\)

    Приклад\(\PageIndex{3}\)

    Окружність сфери становить 26\ pi футів. Що таке радіус сфери?

    Рішення

    Окружність відноситься до окружності великого кола.

    Використання\(C=2\pi r\):

    \(\begin{aligned} 2\pi r&=26\pi \\ r&=13\text{ ft}\end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть площу поверхні сфери радіусом 14 футів.

    Рішення

    Скористайтеся формулою для площі поверхні:

    \(SA=4\pi (14)^{2}\)

    \(=784\pi \text{ ft}^{2}\)\)

    Приклад\(\PageIndex{5}\)

    Знайти обсяг сфери радіусом 6 м.

    Рішення

    Скористайтеся формулою обсягу:

    \(\begin{aligned} V&=\dfrac{4}{3}\pi 63 \\ &=\dfrac{4}{3}\pi (216) \\ &=288\pi \text{ m}^{3}\end{aligned}\)

    Рецензія

    1. Чи існують поперечні перерізи сфери, які не є колом? Поясніть свою відповідь.
    2. Перерахуйте всі частини сфери, які збігаються з колом.
    3. Перерахуйте будь-які частини сфери, яких коло не має.

    Для 4 - 11 знайдіть площу поверхні і обсяг сфери із заданим розмірністю. Залиште свою відповідь з точки зору\(\pi\).

    1. радіусом 8 дюймів.
    2. діаметром 18 см.
    3. радіусом 20 футів.
    4. діаметром 4 м.
    5. радіусом 15 футів.
    6. діаметром 32 дюйма.
    7. окружності\(26\pi \text{ cm}\).
    8. окружності\(50\pi\text{ yds}\).
    9. Площа поверхні кулі дорівнює\(121\pi \text{ in}^{2}\). Що таке радіус?
    10. Обсяг сфери є\(47916\pi \text{ m}^{3}\). Що таке радіус?
    11. Площа поверхні кулі дорівнює\(4\pi \text{ ft}^{2}\). Що таке обсяг?
    12. Обсяг сфери є\(36\pi \text{ mi}^{3}\). Яка площа поверхні?
    13. Знайдіть радіус сфери, яка має об'єм\(335 \text{ cm}^{3}\). Округлите свою відповідь до найближчої сотої.
    14. Знайдіть радіус сфери, яка має площу поверхні\(225\pi \text{ ft}^{2}\).

    Знайдіть площу поверхні і обсяг наступної форми. Залиште свої відповіді в терміні\ pi.

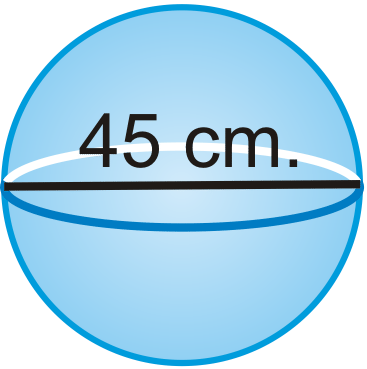
    Ф-д_1а4017Ф7СА67016ЕЕ13КБ88АФ 6770Ф13677Б6279Е728394ФЕ4ФЕ4С59ДА+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.7.

    Лексика

    Термін Визначення
    діаметр Хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.
    Сфера Сфера - це кругле тривимірне тверде тіло. Всі точки на поверхні сфери рівновіддалені від центру сфери.
    Радіус Радіус кола - це відстань від центру кола до краю кола.
    Обсяг Об'єм - це кількість простору всередині меж тривимірного об'єкта.
    Принцип Кавальєрі Заявляється, що якщо два твердих тіла мають однакову висоту і однакову площу поперечного перерізу на кожному рівні, то вони будуть мати однаковий обсяг.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи сфер - Основні

    Види діяльності: Сфери Питання обговорення

    Навчальні посібники: Сфера навчальний посібник

    Практика: Площа поверхні та об'єм сфер

    Реальний світ: Де ми живемо!