Skip to main content
LibreTexts - Ukrayinska

9.24: Обсяг шишок

  1. Last updated
  2. Save as PDF
  • Page ID
    54446

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Об'єм дорівнює площі\(\dfrac{1}{3}\) базового часу висоти.

    F-D_F0578c5f59017e76509175f35fd161FF69a668C09C5AB6DA66128C20+зображення_thumb_листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Пошук об'єму конуса

    Щоб розібратися в обсязі конуса, давайте спочатку розглянемо, як можна порівняти його з іншою солідною фігурою. Найближча суцільна фігура до конусу - циліндр. І конуси, і циліндри мають круглі підстави. Різниця між ними полягає в тому, що циліндр має дві круглі основи, конус має лише одну.

    Ось циліндр і формула знаходження обсягу циліндра.

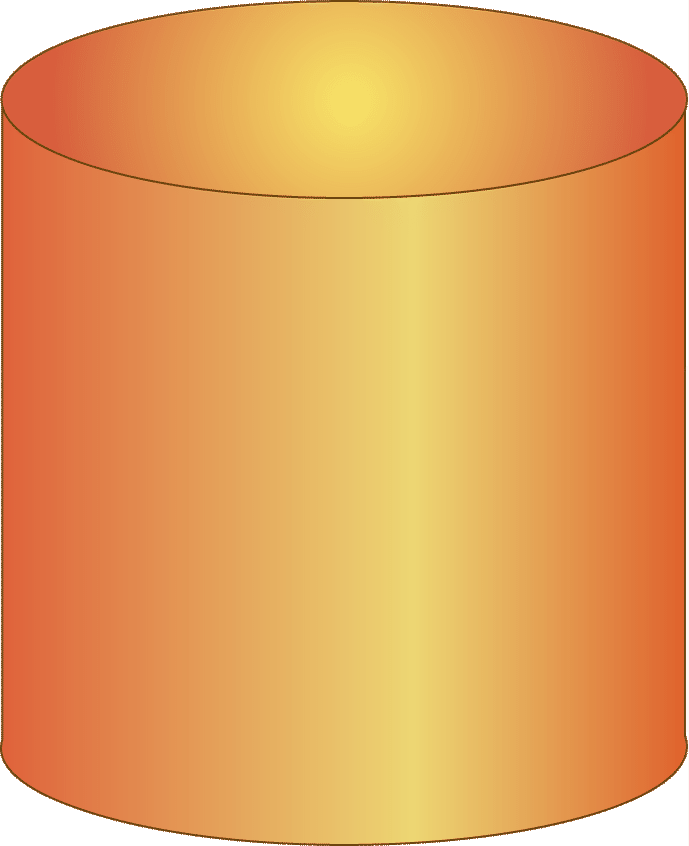
    F-D_242CE1467A 200C1d7251B27556Ф27C9ФД3ДБ4А3137Е0623ФА53001+зображення_крихіткий+зображення_крихіткий_крошечкою.PNG
    Малюнок\(\PageIndex{2}\)

    \(V&=\pi r^{2} h\)

    На зображенні нижче можна побачити, як пов'язані циліндр і конус:

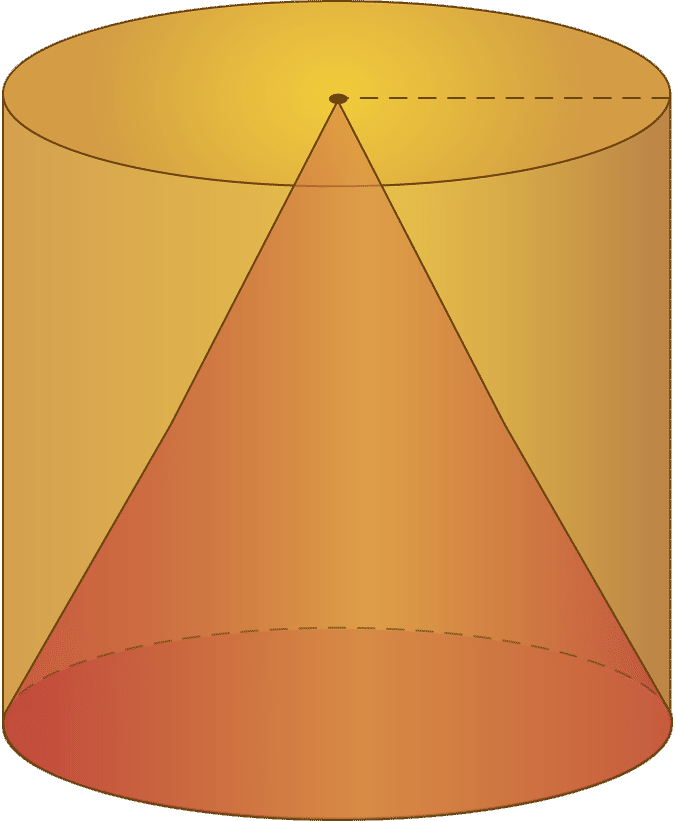
    Ф-д_001А8Б88С2Ф43С7Ф041ДК4Е79ЕА2180Б4Ф0АД Ф4Ф 4Ф0АД 4Ф1Ф7Е2Ф9С1280ДБД+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Щоб знайти об'єм конуса, ви використовуєте формулу, подібну до піраміди, за винятком того, що ви збираєтеся взяти до уваги, що основою конуса є коло. Тому вам потрібно буде знайти площу кола, щоб знайти обсяг конуса. Формула для площі кола є\(\pi r^{2}\). Візьміть цей вимір і помножте його на висоту конуса. Далі, оскільки конус заповнює частину циліндра, помножте виріб на третину.

    \(V&=\dfrac{1}{3} \pi r^{2} h\)

    Давайте розглянемо приклад. Який обсяг конуса нижче?

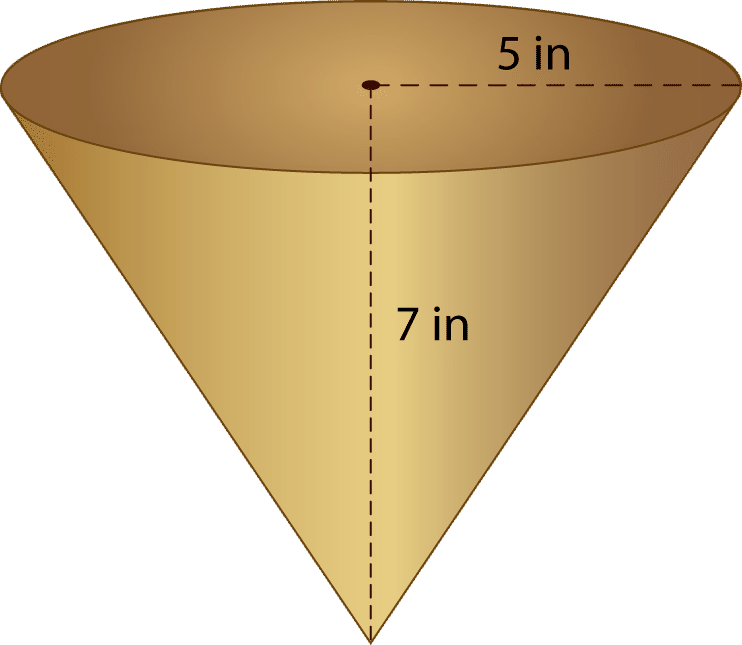
    F-д_3978d22226d822603CE64d9b729FCBC8647154E54C71d43FB96E1D50+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(52)(7) \\ V&=\dfrac{1}{3} (3.14)(25)(7) \\ V&=\dfrac{1}{3} (3.14)(175)\\ V&=\dfrac{549.5}{3} \\ V&=183.16 \text{ in}^{3}\end{aligned}\)

    Відповідь - обсяг конуса - 183,16 кубічних дюймів.

    Давайте розглянемо інший приклад. Знайдіть обсяг наступного конуса.

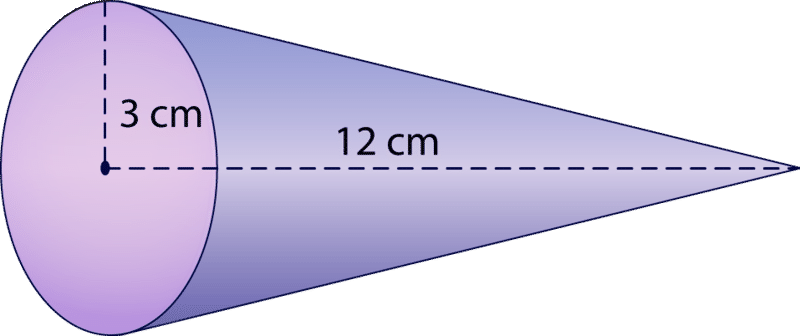
    F-D_3ФД8634Д6А1ЕФ 41А5652Е04С53231733669кС0724А300Ф303СК 761F+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned}V&=\dfrac{1}{3} (3.14)(3^{2})(12) \\ V&=\dfrac{1}{3} (3.14)(9)(12) \\ V&=\dfrac{1}{3} (3.14)(108) \\ V&=\dfrac{339.12}{3} \\ V&=113.04 cm^{3}\end{aligned}\)

    Обсяг конуса дорівнює\(113.04\text{ cm}^3\).

    Приклад\(\PageIndex{1}\)

    Раніше вам давали проблему щодо нових десертних чашок Франсін.

    Їй потрібно з'ясувати обсяг морозива, який поміститься в одну десертну чашку. Діаметр чашки 3 дюйми, а висота - 6 дюймів.

    Рішення

    Спочатку знайдіть значення радіуса, діливши діаметр на 2, і підставити значення для пі, радіуса і висоти конуса в формулу об'єму конуса.

    \(\begin{aligned}r&=1.5 \\ r&=3\divide 2 \\ V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(1.52)(6)\end{aligned}\)

    Далі квадратимо радіус і множимо значення разом.

    \(\begin{aligned}V&=\dfrac{1}{3} (3.14)(1.52)(6) \\ V&=\dfrac{1}{3} (3.14)(2.25)(6) \\ V&=\dfrac{1}{3} (3.14)(13.5) \\ V&=42.393\end{aligned}\)

    Потім розділіть на 3 і запишіть відповідь, не забуваючи включити відповідну одиницю виміру.

    \(\begin{aligned}V&=42.393 \\ V&=14.13 \text{ in}^{3}\end{aligned}\)

    Відповідь - об'єм морозива, який заповнить конусоподібну пустельну чашку Франсін, становить 16,75 кубічних дюймів.

    Приклад\(\PageIndex{2}\)

    Знайдіть обсяг конуса радіусом 2 дюйми і висотою 4 дюйми.

    Рішення

    Спочатку підставляємо значення для пі, радіуса і висоти конуса в формулу об'єму конуса.

    \(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(2^{2})(4)\end{aligned}\)

    Далі квадратимо радіус і множимо значення разом.

    \(\begin{aligned}V&=\dfrac{1}{3} (3.14)(2^{2})(4) \\ V&=\dfrac{1}{3} (3.14)(4)(4) \\ V&=\dfrac{1}{3} (3.14)(16) \\ V&=50.243\end{aligned}\)

    Потім розділіть на 3 і запишіть відповідь, не забуваючи включити відповідну одиницю виміру.

    \(\begin{aligned}V&=\dfrac{50.24}{3} \\ V&=16.75 \text{ in}^{3}\end{aligned}\)

    Відповідь - обсяг конуса - 16,75 кубічних дюймів.

    Приклад\(\PageIndex{3}\)

    Знайдіть обсяг конуса радіусом 5 футів і висотою 8 футів.

    Рішення

    Спочатку підставляємо значення для пі, радіуса і висоти конуса в формулу об'єму конуса.

    \(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(52)(8)\end{aligned}\)

    Далі квадратимо радіус і множимо значення разом.

    \(\begin{aligned}V&=\dfrac{1}{3} (3.14)(52)(8) \\ V&=\dfrac{1}{3} (3.14)(25)(8) \\ V&=\dfrac{1}{3} (3.14)(200) \\ V&=\dfrac{628}{3}\end{aligned}\)

    Потім розділіть на 3 і запишіть відповідь, не забуваючи включити відповідну одиницю виміру.

    \(\begin{aligned}V&=\dfrac{628}{3} \\ V&=209.33 \text{ in}^{3}\end{aligned}\)

    Відповідь - обсяг конуса - 209,33 кубічних дюймів.

    Приклад\(\PageIndex{4}\)

    Конус радіусом 4 м і висотою 9 м.

    Рішення

    Спочатку підставляємо значення для пі, радіуса і висоти конуса в формулу об'єму конуса.

    \(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(4^{2})(9)\end{aligned}\)

    Далі квадратимо радіус і множимо значення разом.

    \(\begin{aligned}V&=\dfrac{1}{3} (3.14)(4^{2})(9) \\ V&=\dfrac{1}{3} (3.14)(16)(9) \\ V&=\dfrac{1}{3} (3.14)(144) \\ V&=\dfrac{452.16}{3}\end{aligned}\)

    Потім розділіть на 3 і запишіть відповідь, не забуваючи включити відповідну одиницю виміру.

    \(\begin{aligned} V&=\dfrac{452.16}{3} \\ V&=150.72 \text{ m}^{3}\end{aligned}\)

    Відповідь - обсяг конуса - 150,72 кубічних метра.

    Рецензія

    Знайдіть обсяг кожного конуса.

    1. Конус радіусом 3 дюйми і висотою 7 дюймів.
    2. Конус радіусом 5 футів і висотою 9 футів.
    3. Конус радіусом 6 метрів і висотою 10 метрів.
    4. Конус радіусом 10 дюймів і висотою 12 дюймів.
    5. Конус радіусом 12 мм і висотою 14 мм.
    6. Конус радіусом 5 футів і висотою 12 футів.
    7. Конус радіусом 4,5 дюйма і висотою 7 дюймів.
    8. Конус радіусом 3,5 дюйма і висотою 5,5 дюймів.
    9. Конус радіусом 7 см і висотою 13 см.
    10. Конус радіусом 8 см і висотою 11 см.
    11. Конус радіусом 7,5 дюймів і висотою 11 дюймів.
    12. Конус радіусом 11,5 дюйма і висотою 15 дюймів.
    13. Конус радіусом 12,5 футів і висотою 15 футів.

    Вирішити кожне слово завдання.

    1. Конус має радіус 6 метрів і висоту 14 метрів. Який її обсяг?
    2. Ємності глазурі для декоратора торта Тіни - це конуси. Кожен контейнер має радіус 2,4 дюйма і висоту 7 дюймів. Якщо Тіна купує контейнери червоної, жовтої та синьої глазурі, скільки глазурі вона придбає?

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 10.15.

    Лексика

    Термін Визначення
    Конус Конус - це суцільна об'ємна фігура з круглим підставою і однією вершиною.
    Піраміда Піраміда - це тривимірний об'єкт з основою, що представляє собою багатокутник і трикутні грані, що зустрічаються в одній вершині.
    Обсяг Об'єм - це кількість простору всередині меж тривимірного об'єкта.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: визначаємо обсяг конуса

    Практика: Обсяг шишок