9.1: Багатогранники
- Page ID
- 54432
3-D фігури, утворені полігонами, що охоплюють області в просторі.
Багатогранник - це тривимірна фігура, яка утворена багатокутниками, що охоплюють область в просторі. Кожен багатокутник у багатограннику - це грань . Відрізок лінії, де перетинаються дві грані, є ребром . Точка перетину двох ребер - це вершина .
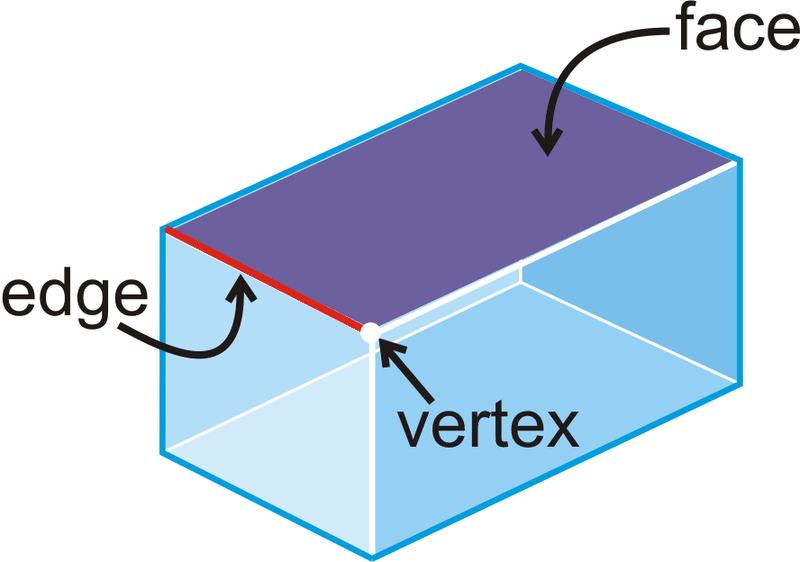
Приклади багатогранників включають куб, призму або піраміду. Конуси, сфери та циліндри не є багатогранниками, оскільки вони мають поверхні, які не є багатокутниками. Нижче наведено більше прикладів багатогранників:
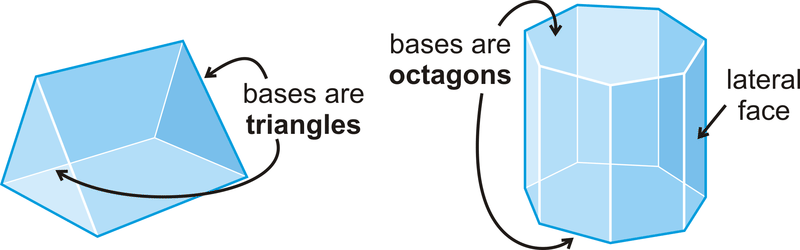
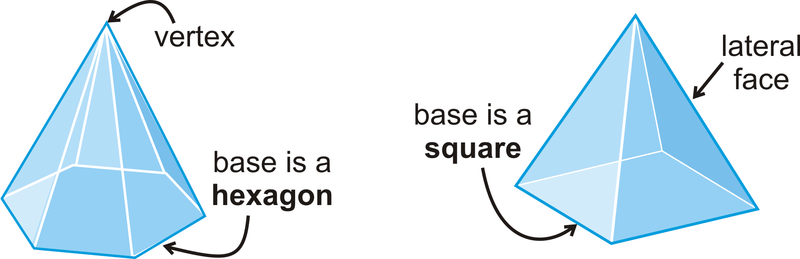
Кількість граней (\(F\)), вершин (\(V\)) та ребер (\(E\)) співвідносяться однаково для будь-якого багатогранника. Їх зв'язок був відкритий швейцарським математиком Леонардом Ейлером, і називається теоремою Ейлера.
Теорема Ейлера:\(F+V=E+2\).
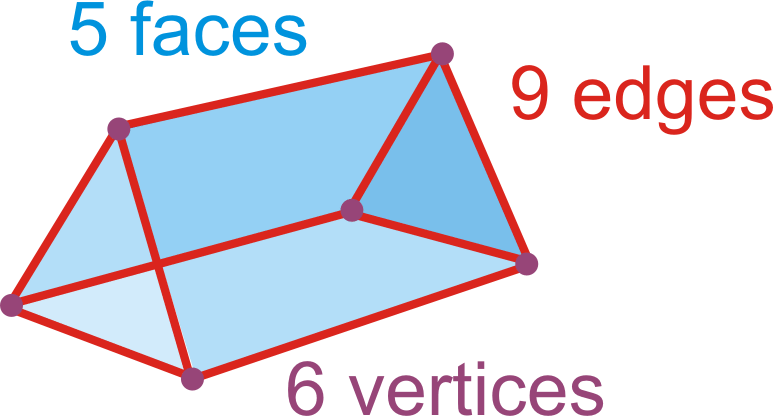
\(Faces+Vertices=Edges+2\)
\(5+6=9+2\)
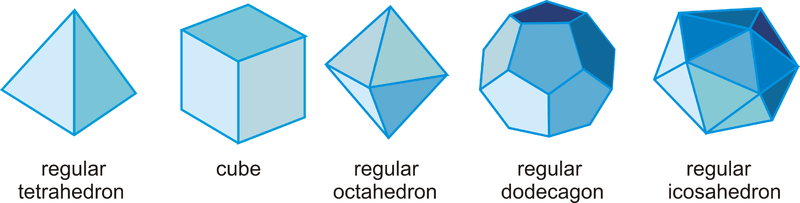
Правильний багатогранник - це багатогранник, де всі грані є конгруентними правильними багатокутниками. Існує лише п'ять правильних багатогранників, званих платонівськими твердими частинами.
- Регулярний тетраедр: 4-гранний багатогранник, а всі грані - рівносторонні трикутники.
- Куб: 6-гранний багатогранник, а всі грані - квадрати.
- Регулярний восьмигранник: 8-гранний багатогранник, а всі грані - рівносторонні трикутники.
- Регулярний додекаедр: 12-гранний багатогранник, а всі грані - правильні п'ятикутники.
- Регулярний ікосаедр: 20-гранний багатогранник, а всі грані - рівносторонні трикутники.
Що робити, якщо вам подарували суцільну об'ємну фігуру, схожу на картонну коробку морозива? Як ви могли визначити, як пов'язані грані, вершини та ребра цієї фігури?
Приклад\(\PageIndex{1}\)
-
Малюнок\(\PageIndex{6}\) -
Малюнок\(\PageIndex{7}\) -

Малюнок\(\PageIndex{8}\)
Рішення
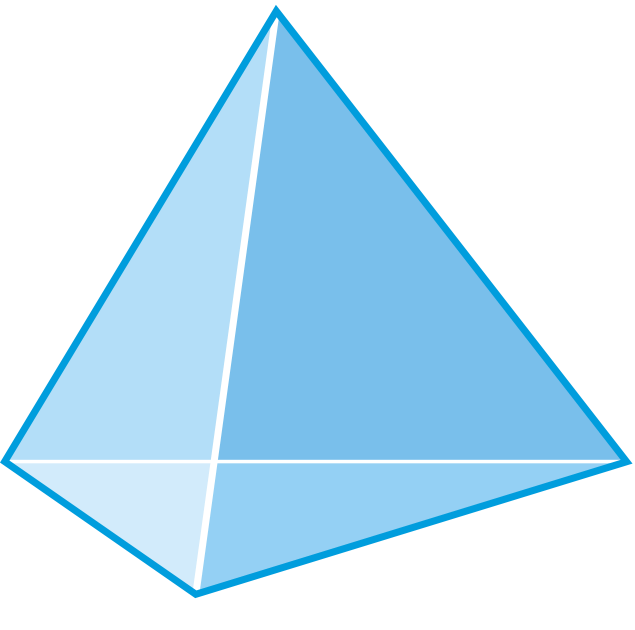
Підстава являє собою трикутник, а всі сторони - трикутники, так що це трикутна піраміда, яка також відома як тетраедр. Є 4 грані, 6 ребер і 4 вершини.
Приклад\(\PageIndex{2}\)
У шестигранному багатограннику є 10 ребер. Скільки вершин має багатогранник?
Рішення
\(V\)Розв'яжіть для в теоремі Ейлера.
\(\begin{aligned} F+V&=E+2 \\ 6+V&=10+2 \\ V&=6\end{aligned} \)
Тому існує 6 вершин.
Приклад\(\PageIndex{3}\)
Маркус підраховує ребра, грані та вершини багатогранника. Він придумує 10 вершин, 5 граней і 12 ребер. Він помилився?
Рішення
Підключіть всі три числа до теореми Ейлера.
\(\begin{aligned} F+V&=E+2 \\ 5+10&=12+2 \\ 15 &\neq 14 \end{aligned}\)
Оскільки дві сторони не рівні, Маркус помилився.
Приклад\(\PageIndex{4}\)
Знайдіть кількість граней, вершин та ребер у восьмикутній призмі.
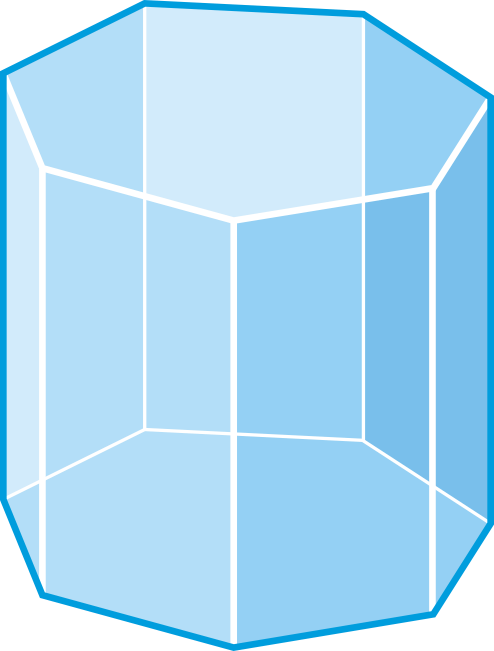
Рішення
Є 10 граней і 16 вершин. Використовуйте теорему Ейлера, щоб вирішити для\(E\).
\(\begin{aligned} F+V&=E+2 \\ 10+16&=E+2 \\ 24&=E \end{aligned}\)
Тому є 24 ребра.
Приклад\(\PageIndex{5}\)
Зрізаний ікосаедр - це багатогранник з 12 правильними п'ятикутними гранями, 20 правильними шестикутними гранями та 90 ребрами. Цей ікосаедр дуже нагадує футбольний м'яч. Скільки вершин у нього? Поясніть свої міркування.

Рішення
Ми можемо використовувати теорему Ейлера для розв'язання кількості вершин.
\(\begin{aligned} F+V&=E+2 \\ 32+V&=90+2 \\ V&=60\end{aligned}\)
Тому він має 60 вершин.
Рецензія
Заповніть таблицю, використовуючи теорему Ейлера.
| Ім'я | Обличчя | Краї | Вершини | |
|---|---|---|---|---|
| 1. | Прямокутна призма | 6 | 12 | |
| 2. | Восьмикутна піраміда | 16 | 9 | |
| 3. | Звичайний ікосаедр | 20 | 12 | |
| 4. | Куб | 12 | 8 | |
| 5. | Трикутна пірамі | 4 | 4 | |
| 6. | Октаедр | 8 | 12 | |
| 7. | Гептагональна призма | 21 | 14 | |
| 8. | Трикутна призма | 5 | 9 |
Визначте, чи є наступні цифри багатогранниками. Якщо так, назвіть фігуру і знайдіть кількість граней, ребер і вершин.
-
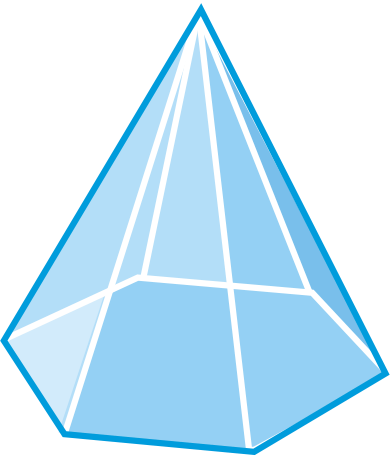
Малюнок\(\PageIndex{11}\) -

Малюнок\(\PageIndex{12}\) -
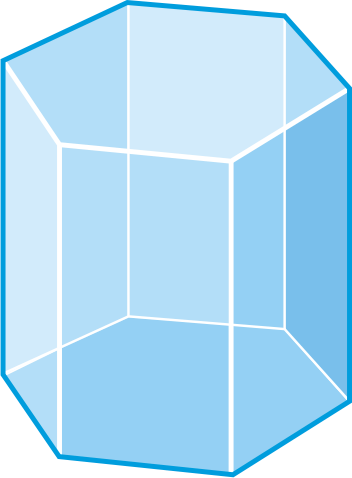
Малюнок\(\PageIndex{13}\) -

Малюнок\(\PageIndex{14}\) -
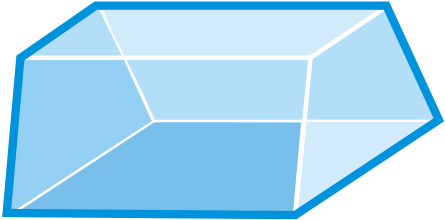
Малюнок\(\PageIndex{15}\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.1.
Додаткові ресурси
Відео: Принципи багатогранників - основні
Види діяльності: Питання обговорення багатогранників
Навчальні посібники: Посібник з вивчення багатогранників
Практика: Багатогранники
Реальний світ: Ролі Poly багатогранник!