9.16: Площа поверхні та об'єм пірамід
- Page ID
- 54444
Площа поверхні і об'єм твердих тіл з основою і бічними гранями, які зустрічаються в загальній вершині.
Піраміди
Піраміда - це суцільне тіло з одним підставою і бічними гранями, які зустрічаються в загальній вершині . Краї між бічними гранями - це бічні ребра . Краї між підставою і бічними гранями є базовими краями .

Правильна піраміда - це піраміда, де основою є правильний багатокутник. Всі правильні піраміди також мають похилу висоту, яка є висотою бічної грані. Неправильна піраміда не має похилої висоти.

Площа поверхні
Площа поверхні - це двовимірне вимірювання, яке є загальною площею всіх поверхонь, які зв'язали тверде тіло. Основною одиницею площі є квадратна одиниця. Для пірамід нам потрібно буде використовувати висоту нахилу, яка позначена l, щоб знайти площу кожної трикутної грані.
Площа поверхні правильної піраміди: Якщо B - площа основи, а n - кількість трикутників, то\(SA=B+\dfrac{1}{2}nbl\).
Сітка показує площу поверхні піраміди. Якщо ви коли-небудь забудете формулу, використовуйте мережу.

Обсяг
Щоб знайти обсяг будь-якого твердого тіла, ви повинні з'ясувати, скільки місця воно займає. Основною одиницею об'єму є кубічна одиниця.
Обсяг піраміди:\(V=\dfrac{1}{3}Bh\) де\(B\) площа підстави.

Що робити, якщо вам дали суцільну об'ємну фігуру з однією основою і бічними гранями, які зустрічаються в загальній вершині? Як ви могли визначити, скільки двовимірного та тривимірного простору займає ця фігура?
Приклад\(\PageIndex{1}\)
Знайдіть похилу висоту квадратної піраміди.

Рішення
Висота нахилу - це гіпотенуза прямокутного трикутника, утвореного висотою і половиною довжини основи. Використовуйте теорему Піфагора.
\(\begin{aligned} 8^{2}+24^{2}&=l^{2} \\ 640&=l^{2} \\ l=\sqrt{640}&=8\sqrt{10}\end{aligned}\)
Приклад\(\PageIndex{2}\)
Знайдіть площу поверхні правильної трикутної піраміди.

Рішення
«Regular» говорить нам, що основа - це рівносторонній трикутник. Давайте намалюємо його і знайдемо його площу.

\(B=\dfrac{1}{2}\cdot 8\cdot 4\sqrt{3}=16\sqrt{3}\)
Площа поверхні становить:
\(SA=16\sqrt{3}+\dfrac{1}{2}\cdot 3\cdot 8\cdot 18=16\sqrt{3}+216\approx 243.71\)
Приклад\(\PageIndex{3}\)
Якщо площа бічної поверхні правильної квадратної піраміди дорівнює\(72\: ft^{2}\) і базовий край дорівнює висоті нахилу. Яка довжина базової кромки?
Рішення
У формулі для площі поверхні площа бічної поверхні дорівнює\(\dfrac{1}{2}nbl\). Ми знаємо, що\(n=4\) і\(b=l\). Давайте вирішимо для\(b\).
\(\begin{aligned} \dfrac{1}{2}nbl&=72\text{ ft}^{2} \\ \dfrac{1}{2}(4)b^{2}&=7^{2} \\ 2b^{2}&=7^{2} \\ b^{2}&=36\\ b&=6 \text{feet}\end{aligned}\)
Приклад\(\PageIndex{4}\)
Знайдіть висоту, а потім обсяг піраміди.

Рішення
У цьому прикладі нам дається висота нахилу. Використовуйте теорему Піфагора.
\(\begin{aligned} 7^{2}+h^{2}&=25^{2} \\ h^{2}&=576 \\ h&=24\end{aligned}\)
\(V=13(142)(24)=1568\text{ units}^{3}\)
Приклад\(\PageIndex{5}\)
Знайдіть обсяг піраміди з прямокутним трикутником в якості основи.
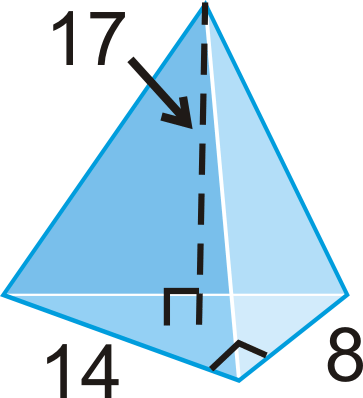
Рішення
Підставою піраміди є прямокутний трикутник. Площа підстави становить\(\dfrac{1}{2}(14)(8)=56\text{ units}^{2}\).
\(V=\dfrac{1}{3}(56)(17)\approx 317.33\text{ units}^{3}\)
Приклад\(\PageIndex{6}\)
Прямокутна піраміда має базову площу\(56\: cm^{2}\) і об'єм\(224\: cm^{3}\). Яка висота піраміди?
Рішення
Скористайтеся формулою гучності і підключіть інформацію, яку нам дали. Потім вирішуйте для висоти.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ 224&=\dfrac{1}{3}\cdot 56h \\ 12&=h \end{aligned}\)
Рецензія
Заповніть пробіли про схему зліва.

- х - це ___________.
- Висота нахилу - ________.
- y - це ___________.
- Висота - ________.
- База - _______.
- Базовий край - ________.
Для питань 7-8 накидайте кожне з наступних твердих тіл і дайте відповідь на питання. Ваші малюнки повинні бути в масштабі, але не один-на-один. Залиште свою відповідь в найпростішій радикальній формі.
- Намалюйте квадратну піраміду з довжиною краю 9 дюймів і 12 у висоту. Знайдіть висоту нахилу.
- Намалюйте рівносторонню піраміду трикутника з довжиною краю 6 см і висотою 6 см. Яка висота підстави?
Знайдіть висоту нахилу, l, однієї бічної грані в кожній піраміді. Округлите свою відповідь до найближчої сотої.
-

Малюнок\(\PageIndex{11}\) -

Малюнок\(\PageIndex{12}\)
Знайдіть площу поверхні і обсяг правильної піраміди. Округляйте свої відповіді до найближчих сотих.
-

Малюнок\(\PageIndex{13}\) -

Малюнок\(\PageIndex{14}\) -

Малюнок\(\PageIndex{15}\) -

Малюнок\(\PageIndex{16}\) -
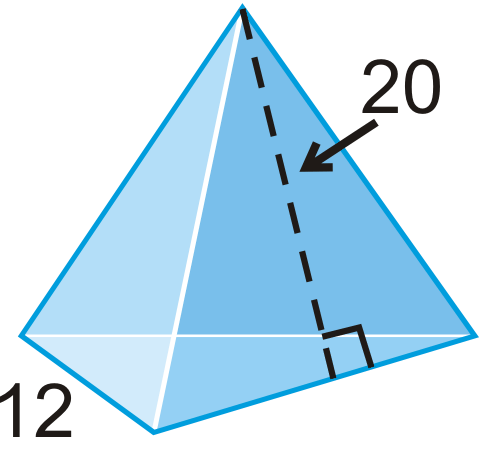
Малюнок\(\PageIndex{17}\) -

Малюнок\(\PageIndex{18}\) - Правильний тетраедр має чотири рівносторонніх трикутника як його грані.
- Знайдіть висоту однієї з граней, якщо довжина ребра дорівнює 6 одиницям.
- Знайдіть область одного особи.
- Знайдіть загальну площу поверхні правильного тетраедра.
- Якщо площа поверхні квадратної піраміди становить,\(40\text{ ft}^{2}\) а базовий край становить 4 фути, яка висота нахилу?
- Якщо бічна площа квадратної піраміди становить,\(800\text{ in}^2\) а висота нахилу становить 16 дюймів, яка довжина базового краю?
- Якщо бічна площа правильної піраміди трикутника є,\(252\text{ in}^2\) а базовий край - 8 дюймів, яка висота нахилу?
- Обсяг квадратної піраміди становить 72 квадратних дюймів, а базовий край - 4 дюйми. Яка висота?
- Обсяг піраміди трикутника\(170\text{ in}^3\) дорівнює, а площа основи -\(34\text{ in}^2\). Яка висота піраміди?
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 11.5.
Лексика
| Термін | Визначення |
|---|---|
| бічні краї | Краї між бічними гранями призми. |
| бічні грані | Небазові грані призми. |
| Піраміда | Піраміда - це тривимірний об'єкт з основою, що представляє собою багатокутник і трикутні грані, що зустрічаються в одній вершині. |
| правильна піраміда | це піраміда, де основою є правильний багатокутник. Всі правильні піраміди також мають похилу висоту, яка є висотою бічної грані. |
| Конус | Конус являє собою суцільну об'ємну фігуру з круглим підставою і однією вершиною. |
| Вершина | Вершина - це точка перетину ліній або променів, які утворюють кут. |
| Обсяг | Об'єм - це кількість простору всередині меж тривимірного об'єкта. |
| Принцип Кавальєрі | Заявляється, що якщо два твердих тіла мають однакову висоту і однакову площу поперечного перерізу на кожному рівні, то вони будуть мати однаковий обсяг. |
| Базовий край | Базова кромка - це край між підставою і бічними гранями призми. |
| Висота нахилу | Висота нахилу - це висота бічної грані піраміди. |
| Апофем | Апофемом правильного багатокутника є перпендикулярний відрізок від центральної точки багатокутника до середини однієї з його сторін. |