9.17: Обсяг пірамід
- Page ID
- 54458
Об'єм дорівнює площі\(\dfrac{1}{3}\) базового часу висоти.

Майкл та Хуаніта зацікавлені в кількості піску, необхідного для побудови пісочної піраміди такого розміру, який вони бачать під час експонату піщаної скульптури. Вони ретельно вимірюють ширину квадратної основи пісочної піраміди, яка становить 4 фути, і висоту піраміди, яка становить 5 футів. Скільки піску потрібно для будівництва цієї пісочної піраміди?
У цьому понятті ви дізнаєтеся, як розрахувати обсяг піраміди.
Пошук обсягу піраміди
Піраміди - це суцільні форми, які існують в тривимірному просторі. Піраміда має сторони, які є трикутними гранями і підставою, яка може бути будь-якої форми.

Обсяг - це міра того, скільки місця займає або займає тривимірна фігура. Обсяг вимірюється в кубічних одиницях, тому що ви маєте справу з трьома вимірами: довжиною, шириною та висотою.
Почати розуміти обсяг піраміди можна, порівнявши піраміду з аналогічною їй фігурою. Ви знаєте, що призма має довжину, ширину і висоту. Паралельні підстави призми можуть бути будь-яким багатокутником. Цей має квадратну основу; так його називають кубом.

Тепер подумайте про піраміду. Він має базу, яка може бути будь-яким багатокутником. Підставою цієї піраміди є квадрат.

Вони обидва схожі, враховуючи, що мають квадратні основи. Подумайте про обсяг піраміди, дивлячись на обсяг куба або призми. Подивіться на цю картинку, яка демонструє відношення куба до квадратної піраміди:

Щоб знайти обсяг цього куба, помножте базу на ширину на висоту. Щоб знайти обсяг піраміди, візьміть площу\(B\) підстави, і помножте її на висоту, а потім помножте її на\(\dfrac{1}{3}\). Ось формула знаходження обсягу піраміди.
\(\(V=\dfrac{1}{3}Bh\)
Слід пам'ятати про те, що піраміди можуть бути складними, оскільки вони можуть мати багато різних основ. \(B\)в формулі означає, що потрібно знайти площу підстави. Якщо підставою є квадрат, потрібно буде скористатися формулою площі квадрата,\(B=s^2\). Якщо основа - прямокутник, площа підстави дорівнює\(B=lw\). Якщо підставою є трикутник, скористайтеся формулою\(B=\dfrac{bh}{2}\). Переконавшись, що у вас є правильна формула, має важливе значення у вашій роботі з пірамідами.
Давайте розглянемо приклад. Який обсяг піраміди нижче?
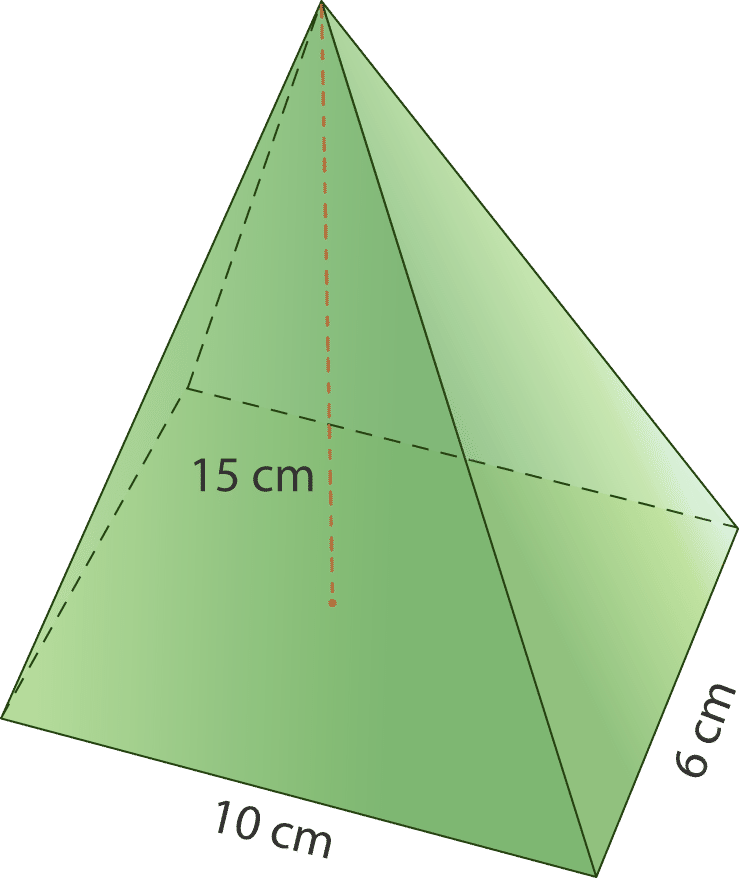
Для початку визначитеся, якої форми має підставу піраміди. Одна сторона - 10 сантиметрів, а інша - 6 сантиметрів, тому це повинен бути прямокутник. Використовуйте формулу площі для прямокутників, щоб знайти B, базову площу.
\(\begin{aligned} B&=lw \\ B&=10(6) \\ B&=60\text{ cm}^{2}\end{aligned}\)
Площа підстави цієї піраміди становить 60 квадратних сантиметрів. Тепер помножте це на висоту і 13 за формулою.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(60)(15) \\ V&=\dfrac{900}{3} \\ V&=300\text{ cm}^{3}\end{aligned}\)
Відповідь - обсяг піраміди становить 300 кубічних сантиметрів.
Пам'ятайте, ви вимірюєте обсяг в трьох вимірах, тому пишіть відповідь в кубічних одиницях.
Давайте розглянемо інший приклад.
Обсяг малюнка знайдіть нижче.

Цього разу основою є трикутник, тому вам потрібно буде використовувати формулу площі для трикутників, щоб знайти базову площу. Будьте обережні, щоб не переплутати висоту базового трикутника з висотою всієї піраміди.
\(\begin{aligned} B&=\dfrac{1}{2}bh\\ B&=\dfrac{1}{2}(8)(3) \\ B&=\dfrac{24}{2} \\ B&=12 in^{2}\end{aligned}\)
Площа основи для цієї трикутної піраміди становить 12 квадратних дюймів. Помістіть це в формулу і вирішіть для V, об'єму.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(12)(17) \\ V&=\dfrac{204}{3} \\ V&=68\text{ in}^{3}\end{aligned}\)
Відповідь - обсяг цієї піраміди становить 68 кубічних дюймів.
Приклад\(\PageIndex{1}\)
Раніше вам давали проблему щодо інтересу Майкла та Хуаніти до піраміди піщаної скульптури.
Вони хочуть з'ясувати обсяг піску, необхідний для створення пісочної скульптурної піраміди з основою 4 фути і висотою 5 футів:
Рішення
Спочатку визначте форму підстави і скористайтеся правильною формулою, щоб знайти площу підстави. Оскільки основою є квадрат, скористайтеся формулою площі для квадратів, щоб знайти площу основи.
\(\begin{aligned} B&=s^{2} \\ B&=(4)^{2} \\ B&=16\text{ ft}^{2}\end{aligned}\)
Площа підстави піраміди становить 16 квадратних сантиметрів.
Далі включаємо площу підстави, а висоту піраміди в формулу обсягу піраміди і множимо значення разом.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(16)(5) \\ V&=803\end{aligned}\)
Потім розділіть на 3 для відповіді, переконавшись, що включіть відповідну одиницю виміру.
\(\begin{aligned}V&=803 \\ V&=26.67\text{ ft}^{3}\end{aligned}\)
Відповідь полягає в тому, що обсяг піску, необхідний для створення пісочної скульптури піраміди, становить 26,67 кубічних футів.
Приклад\(\PageIndex{2}\)
Феліс купила свічку нижче на день народження своєї подруги. На упаковці написано, що свічка горить одну годину на кожні 20 кубічних сантиметрів воску. Який обсяг свічки, щоб Феліс міг розібратися, як довго вона буде горіти?

Рішення
Спочатку визначте форму підстави і скористайтеся правильною формулою, щоб знайти площу підстави. Оскільки основою є квадрат, ви використовуєте формулу площі для квадратів, щоб знайти базову площу.
\(\begin{aligned}B&=s^{2} \\ B&=(12)^{2} \\ B&=144\text{ cm}^{2}\end{aligned}\)
Площа підстави піраміди становить 144 квадратних сантиметри.
Далі включаємо площу підстави, а висоту піраміди в формулу обсягу піраміди і множимо значення разом.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(144)(24) \\ V&=\dfrac{3456}{3}\end{aligned}\)
Потім розділіть на 3 для відповіді, переконавшись, що включіть відповідну одиницю виміру.
\(\begin{aligned} V&=\dfrac{3456}{3} \\ V&=1,152\text{ cm}^{3}\end{aligned}\)
Відповідь - обсяг свічки - 1,152 кубічних см.
Приклад\(\PageIndex{3}\)
Знайдіть обсяг квадратної піраміди з підставою 8 см і висотою 6 см.
Рішення
Спочатку визначте форму підстави і скористайтеся правильною формулою, щоб знайти площу підстави. Основа є квадратом, тому використовуйте формулу площі для квадратів, щоб знайти базову площу.
\(\begin{aligned} B&=s^{2} \\ B&=(8)^{2} \\ B&=64\text{ cm}^{2}\end{aligned}\)
Площа підстави піраміди становить 64 квадратних сантиметри.
Далі включаємо площу підстави, а висоту піраміди в формулу обсягу піраміди і множимо значення разом.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(64)(6) \\ V&=\dfrac{384}{3}\end{aligned} \)
Потім розділіть на 3 для відповіді, переконавшись, що включіть відповідну одиницю виміру.
\(\begin{aligned} V&=\dfrac{384}{3} \\ V&=128\text{ cm}^{3}\end{aligned}\)
Відповідь - обсяг піраміди дорівнює 128 кубічних см.
Приклад\(\PageIndex{4}\)
Знайдіть обсяг прямокутної піраміди довжиною 10 см, шириною 8 см і висотою 9 см.
Рішення
Спочатку визначте форму підстави і скористайтеся правильною формулою, щоб знайти площу підстави. Оскільки основою є прямокутник, скористайтеся формулою площі для квадратів, щоб знайти площу основи.
\(\begin{aligned} B&=lw \\ B&=(10)(8) \\ B&=80\text{ cm}^{2}\end{aligned}\)
Площа підстави піраміди становить 80 квадратних сантиметрів.
Далі включаємо площу підстави, а висоту піраміди в формулу обсягу піраміди і множимо значення разом.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(80)(9) \\ V&=\dfrac{720}{3}\end{aligned}\)
Потім розділіть на 3 для відповіді, переконавшись, що включіть відповідну одиницю виміру.
\(\begin{aligned} V&=\dfrac{720}{3} \\ V&=240\text{ cm}^{3}\end{aligned}\)
Відповідь - обсяг піраміди дорівнює 240 кубічних см.
Приклад\(\PageIndex{5}\)
Знайдіть обсяг квадратної піраміди з підставою 5,5 дюйма і висотою 4 дюйма.
Рішення
Спочатку визначте форму підстави і скористайтеся правильною формулою, щоб знайти площу підстави. Основа є квадратом, тому використовуйте формулу площі для квадратів, щоб знайти базову площу.
\(\begin{aligned} B&=s^{2} \\ B&=(5.5)^{2} \\ B&=30.25 in^{2}\end{aligned} \)
Площа підстави піраміди становить 30,25 квадратних сантиметрів.
Далі включаємо площу підстави, а висоту піраміди в формулу обсягу піраміди і множимо значення разом.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(30.25)(4) \\ V&=\dfrac{121}{3}\end{aligned}\)
Потім розділіть на 3 для відповіді, переконавшись, що включіть відповідну одиницю виміру.
\(\begin{aligned} V&=\dfrac{121}{3} \\ V&=40.33\text{ in}^{3}\end{aligned}\)
Відповідь - обсяг піраміди дорівнює 40,33 кубічних дюймів.
Рецензія
Знайдіть обсяг кожної з наступних пірамід.
- Квадратна піраміда з основою 6 футів і висотою 9 футів.
- Квадратна піраміда з підставою 8 м і висотою 10 м.
- Квадратна піраміда з підставою 11 дюймів і висотою 13 дюймів.
- Квадратна піраміда з основою 9 футів і висотою 14 футів.
- Квадратна піраміда з основою 4,5 дюйма і висотою 5 дюймів.
- Прямокутна піраміда з довжиною основи 4 дюйма, шириною основи 3 дюйма і висотою 5 дюймів.
- Прямокутна піраміда з довжиною основи 5 футів, шириною основи 4 фути і висотою 6 футів.
- Прямокутна піраміда з довжиною підстави 7 м, шириною підстави 4 м і висотою 9 м.
- Трикутна піраміда з базовою довжиною 5 дюймів і базовою висотою 4 дюйми з пірамідою висотою 6 дюймів.
- Трикутна піраміда з довжиною основи 8 футів і базовою висотою 7 футів з пірамідою висотою 9 футів.
- Квадратна піраміда з основою 8 футів і висотою 4 фути.
- Прямокутна піраміда довжиною 5 дюймів, шириною 4 дюйма і висотою 6 дюймів.
- Квадратна піраміда з основою 3.5 футів і висотою 6.5 футів.
- Квадратна піраміда з основою 6,5 футів і висотою 8.5 футів.
- Прямокутна піраміда шириною 4 фути, довжиною 6 футів і висотою 7,5 футів.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.14.
Лексика
| Термін | Визначення |
|---|---|
| Конус | Конус являє собою суцільну об'ємну фігуру з круглим підставою і однією вершиною. |
| Піраміда | Піраміда - це тривимірний об'єкт з основою, що представляє собою багатокутник і трикутні грані, що зустрічаються в одній вершині. |
| Обсяг | Об'єм - це кількість простору всередині меж тривимірного об'єкта. |
Додаткові ресурси
Інтерактивний елемент
Відео: Обсяг піраміди - огляд
Практика: Обсяг пірамід