Skip to main content
LibreTexts - Ukrayinska

9.12: Обсяг призм

  1. Last updated
  2. Save as PDF
  • Page ID
    54523

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використовуйте формулу\(V = Bh\)

    F-D_E706647DB9AFB6C71FA33073DE2C3407C080736BE487C560002D8EFE+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Карен і Ленс будують дитячий майданчик на задньому дворі для своїх двох дітей. У них встановлена гойдалка, карусель та пісочниця. Ленс збирається в магазин, щоб купити пісок для пісочниці і повинен знати, скільки піску він може вмістити. Пісочниця шириною 6 футів, довжиною 8 футів і глибиною 1 футів. Як Ланс може використовувати формулу для обчислення загального обсягу цієї пісочниці?

    У цьому понятті ви навчитеся знаходити обсяги прямокутних і трикутних призм за допомогою формул.

    Знаходження об'єму призм

    Обсяг - це кількість простору всередині суцільної фігури.

    Наповнення твердих фігур кубиками - простий, легкий спосіб зрозуміти обсяг. Якщо ви вмієте рахувати кубики, то зможете розібратися з обсягом. Однак іноді вам доведеться з'ясувати об'єм призми, коли всередині неї немає жодних кубиків.

    Погляньте на призму нижче.

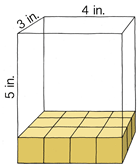
    F-D_BB69БК6А9AD4D591B2AAAE14650D58E5E98FB0027E75E75E8A578БК+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    Ця прямокутна призма має висоту 5 дюймів, ширину 3 дюйми і довжину 4 дюйми.

    Ось формула знаходження об'єму цього типу призми.

    \(V=Bh\)

    B означає площу підстави, довжина якої перевищує ширину, а h означає висоту.

    Отже, спочатку з'ясуємо площу підстави.

    \(A=3\times 4=12\)

    Далі множимо\(B\) на\(h\).

    \(\begin{aligned} h&=5\\ V&=12\times 5=60\end{aligned}\)

    Обсяг становить 60 кубічних дюймів або\(in^{3}\). Пам'ятайте, обсяг знаходиться в кубічних одиницях.

    Давайте розглянемо інший приклад. Знайдіть обсяг, використовуючи формулу гучності.

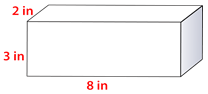
    F-D_E00EBBFE29129F430BCCF4А64ФЦБФ56FE14D6CCF0764C653AE0+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    \(V=Bh\)

    Спочатку намалюйте площу підстави.

    Площа підстави становить\(2\times 8=16\)

    Далі помножте B на h Висота - 3 дюйми.

    \(\begin{aligned} V&=16\times 3 \\ V&=48\: \text{ in}^{3}\end{aligned}\)

    Обсяг цієї прямокутної призми дорівнює\(48\:\text{ in}^{3}\).

    Можна використовувати ту ж формулу для знаходження обсягу трикутної призми. Крім цього часу, площа підстави - це трикутник, а не прямокутник.

    Погляньте на трикутну призму нижче.

    F-D_4C47F875B492B60957 А09А92А9Д487 ЕАЕЕ994А1Ф707ABCA8F3D6958+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    Щоб знайти обсяг трикутної призми, помножте площу підстави (\(B\)) на висоту призми.

    \(V=Bh\)

    Спочатку знайдіть площу трикутної основи, використовуючи формулу площі трикутника.

    \(\begin{aligned} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(15\times 6) \\ A&=\dfrac{1}{2}(90) \\ A&=45\:\text{ sq. units}\end{aligned}\)

    Далі множимо це на висоту.

    \(\begin{aligned} V&=Bh \\ V&=(45)h \\ V&=45(2) \\ V&=90\text{ cubic centimeters} or \text{ cm}^{3}\end{aligned}\)

    Обсяг призми дорівнює\(90\text{ cm}^{3}\).

    Приклад\(\PageIndex{1}\)

    Раніше вам дали проблему про пісочницю Ленса і Карен.

    Пісочниця шириною 6 футів, довжиною 8 футів і глибиною 1 футів. Ленсу потрібно знати обсяг.

    Рішення

    Щоб знайти обсяг пісочниці, яка представляє собою призму з одним з її підстав, скористайтеся наступною формулою.

    \(V=Bh\)

    Спочатку підставляємо в задані значення. Пам'ятайте, B - довжина на ширину.

    \(\begin{aligned} V&=(8\times 6)(1)\\ V&=48\text{ ft}^{3}\end{aligned}\)

    Це загальний обсяг.

    Далі, щоб дізнатися, скільки піску йому потрібно для заповнення пісочниці наполовину, розділіть загальний обсяг на 2.

    \(48\divide 2=24\)

    Ленс потребує 24 кубічних футів піску, щоб заповнити пісочницю на півдорозі.

    Приклад\(\PageIndex{2}\)

    Знайдіть обсяг призми.

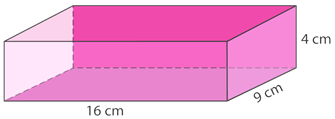
    F-D_6851 БК8ФД Д 2 ББДДДА4ФД51Е4АФ9АФА4063А1Ф418C3987DDE3B8CE2FE8+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Щоб знайти обсяг призми, скористайтеся наступною формулою.

    \(V=Bh\)

    Спочатку підставляємо в задані значення. Пам'ятайте, B - довжина на ширину.

    \(\begin{aligned} V&=(16\times 9)(4) \\ V&=576\text{ cm}^{3}\end{aligned}\)

    Відповідь є\(576\text{ cm}^{3}\).

    Приклад\(\PageIndex{3}\)

    Знайдіть обсяг призми.

    F-D_FB546C5BB79534967E2E892 C8962A7D51481ED4CBE462E67F6ADEFE+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{6}\)

    Рішення

    По-перше, щоб знайти обсяг призми, скористайтеся наступною формулою.

    \(V=Bh\)

    Далі підставляємо в задані значення. Пам'ятайте, B - довжина на ширину. Це квадратний куб, тому довжина, ширина і висота однакові.

    \(\begin{aligned} V&=(5\times 5)(5) \\V&=125\text{ in}^{3}\end{aligned}\)

    Відповідь є\(125\text{ in}^{3}\).

    Приклад\(\PageIndex{4}\)

    Знайдіть обсяг призми.

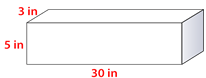
    F-D_A1D9 ЕФ2ДБАФ 2702Б00C19B9A0E09E9E22D8E946CBF10C3D89AC3E+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{7}\)

    Рішення

    По-перше, щоб знайти обсяг призми, скористайтеся наступною формулою.

    \(V=Bh\)

    Спочатку підставляємо в задані значення. Пам'ятайте, B - довжина на ширину.

    \(\begin{aligned} V&=(30\times 5)(3) \\ V&=450\text{ in}^{3}\end{aligned}\)

    Відповідь є\(450\text{ in}^{3}\).

    Приклад\(\PageIndex{5}\)

    Знайдіть обсяг призми.

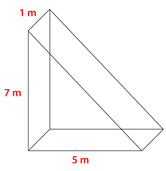
    F-D_133EE8D3DB357578F6D5987CA76E0876E549B273B687D4E1E972343+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{8}\)

    Рішення

    Щоб знайти обсяг трикутної призми, помножте площу підстави (В) на висоту призми.

    \(V=Bh\)

    Спочатку знайдіть площу трикутної основи, використовуючи формулу площі трикутника.

    \(\begin{aligned} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(5\times 7) \\ A&=\dfrac{1}{2}(35) \\ A&=17.5 \text{ sq. m} \end{aligned}\)

    Далі множимо це на висоту.

    \(\begin{aligned} V&=Bh \\ V&=(17.5)1 \\ V&=17.5\text{ cm}^{3}\end{aligned}\)

    Обсяг призми дорівнює\(17.5\text{ cm}^{3}\).

    Рецензія

    Знайдіть обсяг кожної прямокутної призми. Не забудьте позначити свою відповідь кубічними одиницями.

    1. Довжина = 5 дюймів, ширина = 3 дюйма, висота = 4 дюйми
    2. Довжина = 7 м, ширина = 6 м, висота = 5 м
    3. Довжина = 8 см, ширина = 4 см, висота = 9 см
    4. Довжина = 8 см, ширина = 4 см, висота = 12 см
    5. Довжина = 10 футів, ширина = 5 футів, висота = 6 футів
    6. Довжина = 9 м, ширина = 8 м, висота = 11 м
    7. Довжина = 5,5 дюйма, ширина = 3 дюйма, висота = 5 дюймів
    8. Довжина = 6,6 см, ширина = 5 см, висота = 7 см
    9. Довжина = 7 футів, ширина = 4 фути, висота = 6 футів
    10. Довжина = 15 м, ширина = 8 м, висота = 10 м

    Знайдіть обсяг кожної трикутної призми. Пам'ятайте, що h\) означає висоту трикутної основи, а H\) означає висоту всієї призми.

    1. \(b=6\text{ in}\),\(h=4\text{ in}\),\(H=5\text{ in}\)
    2. \(b=7\text{ in}\),\(h=5\text{ in}\),\(H=9\text{ in}\)
    3. \(b=10\text{ m}\),\(h=8\text{ m}\),\(H=9\text{ m}\)
    4. \(b=12\text{ m}\),\(h=10\text{ m}\),\(H=13\text{ m}\)
    5. \(b=8\text{ cm}\),\(h=6\text{ cm}\),\(H=9\text{ cm}\)

    Відповідь true або false на кожне з наступних питань.

    1. Обсяг - це кількість простору, яке фігура може утримувати всередині нього.
    2. Обсяг прямокутної призми завжди більше обсягу куба.
    3. Обсяг трикутної призми менше прямокутної призми з таким же розміром підстави.
    4. Художник повинен знати площу поверхні будинку, щоб правильно виконувати свою роботу.
    5. Якщо Маркус покриває свою книгу обкладинкою книги, Маркус покриває площу поверхні книги.

    Лексика

    Термін Визначення
    Чистий Сітка - це діаграма, яка показує «сплющений» вигляд твердого тіла. У сітці кожна грань і основа показані з усіма її розмірами. Сітка також може служити візерунком для побудови об'ємного твердого тіла.
    Прямокутна призма Прямокутна призма - це призма, складена з двох прямокутних підстав і чотирьох прямокутних граней.
    Площа поверхні Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта.
    Трикутна призма Трикутна призма - це призма, складена з двох трикутних підстав і трьох прямокутних граней.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Об'єм твердої геометрії

    Практика: Обсяг призм