Skip to main content
LibreTexts - Ukrayinska

9.11: Площа поверхні призм

  1. Last updated
  2. Save as PDF
  • Page ID
    54516

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використовуйте формули, щоб знайти площу поверхні прямокутної призми і трикутної призми.

    Площа поверхні трикутних призм

    F-D_9674 Б4Д9БФФ 4014Б1912855Б128С300А92А876Б8А59837406509БД+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Макс купив світлу призму для своєї мами на День матері. Він хоче розібратися, скільки потрібно обгорткового паперу, щоб його обернути. Для цього йому потрібно з'ясувати площу поверхні подарунка. Трикутний кінець має підставу 3 см і висоту 4 см. Довжина кожної сторони становить 6 см, а висота призми (довжина прямокутної сторони) - 8 см. Яка площа поверхні подарунка, який Макс купив для своєї мами?

    У цьому понятті ви дізнаєтеся, як розрахувати площу поверхні трикутної призми.

    Знаходження площі поверхні трикутної призми

    Площа - це простір, який міститься в двовимірній фігурі. Площа поверхні - це загальна площа всіх сторін і граней тривимірної фігури. Щоб знайти площу поверхні, обчислюється площа кожної грані, а потім складають ці ділянки разом.

    Один із способів зробити це - використовувати сітку, так як сітка - це двовимірне зображення тривимірного твердого тіла, або розгорнута картинка твердого тіла.

    Яка площа поверхні малюнка нижче?

    F-D_2C7281036FB9E2E4B855b7B4750b5948dc8f90c2756455cccee2280+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    Сітка для цієї трикутної призми виглядає наступним чином:

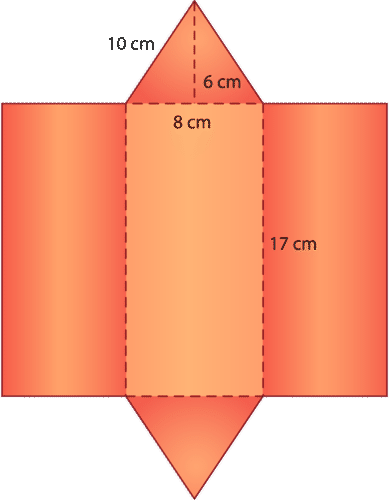
    F-D_C710139258D743633D15234479E6655AB744F71BBF7A28FD699+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    Тепер давайте заповнимо мірки для сторін кожної грані, щоб обчислити їх площу. Трикутні призми мають власну формулу знаходження площі поверхні, оскільки вони мають дві трикутні грані навпроти один одного.

    Формула\( A=\dfrac{1}{2}bh\) використовується для знаходження площі вершини і підстав трикутних граней, де A = площа, b = підстава, а h = висота. Формула\(A=lw\) використовується для знаходження площі трьох прямокутних бічних граней, де A = площа, l = довжина, а w = ширина.

    Включивши виміри, які наведені в сітці, обчислити площу кожної грані. Не забудьте використовувати правильну формулу площі для трикутників і прямокутників.

    \ (\ begin {масив} {lllll}
    \ текст {Нижня грань} &\ текст {Верхня грань} &\ текст {сторона} &\ текст {сторона} &\ текст {сторона}\\
    A=\ frac {1} b & A=\ frac {1} {2} b h & A = L w & A = L w & A = L w\\
    \ frac {1} {2} (8) (6) + &\ гідророзриву {1} {2} (8) (6) + & 17\ разів 10+ & 17\ разів 10+ & 17\ разів 8\
    24 & + & 24 & + & + & 170 & + & 170 & + & + & 136\\
    = 524\ mathrm {~ см} ^ {2} & &
    \ кінець {масив}\)

    Коли ви додаєте ці значення разом, ви отримаєте площу поверхні 524 квадратних сантиметрів для цієї трикутної призми.

    \(SA=bh+(s_{1}+s_{2}+s_{3})H\)

    Ви також можете використовувати одну формулу для обчислення площі поверхні трикутної призми, яка може заощадити час протягом процесу використання сітки для отримання площ:

    де b = основа; h = висота трикутника; s_ {1}\), s_ {2}\), і s_ {3}\) = довжина кожної сторони підстави трикутника, а H = висота призми (яка є довжиною прямокутників).

    Спочатку знайдіть площу двох трикутних граней. Кожне обличчя матиме площу 12bh. Пам'ятайте, ви можете використовувати формулу для обчислення площі пари граней. Таким чином, ви можете подвоїти цю формулу, щоб знайти площу обох трикутних граней відразу, що призводить до формули 2 (12bh). 2 помножений на 12 дорівнює 1, або скасовує один одного, і ви залишаєтеся з BH.

    Далі потрібно обчислити площу кожної з прямокутних бічних граней. Довжина кожного прямокутника така ж, як висота призми, так називайте це H. Ширина кожного прямокутника насправді така ж, як і сторони трикутної основи. Замість того, щоб множити довжину і ширину для кожного прямокутника, ви можете об'єднати цю інформацію. Так як існує 3 прямокутних ширини (всі рівні сторонам трикутників), помножте периметр трикутної основи на висоту прямокутників H, що дасть площу всіх трьох прямокутників.

    Якщо скласти ці частини разом - площа основ і площа бічних граней - ви отримаєте таку формулу:

    \(SA=bh+(s_{1}+s_{2}+s_{3})H\)

    де bh = площа вершини трикутника і підстави, а (\(s_{1}+s_{2}+s_{3})H\)= площа прямокутних бічних граней.

    Пам'ятайте, що висота трикутної основи (\(h\)) не обов'язково збігається з висотою призми (H).

    Приклад\(\PageIndex{1}\)

    Раніше вам давали проблему з приводу подарунка Макс купив для своєї мами.

    Трикутний кінець має підставу 3 см і висоту 4 см. Довжина кожної сторони становить 6 см, а висота призми (довжина прямокутника) - 8 см. Яка площа поверхні цієї трикутної призми?

    Рішення

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=3(4)+(3+6+6)(8)\end{aligned}\)

    Далі множимо підставу на висоту на площу трикутників (bh), і складаємо їх три сторони (\(s_{1} + s_{2} + s_{3}\)).

    \(SA=12+15(8)\)

    Потім помножте суму сторін трикутника на висоту призми (H\)) і складіть значення разом для відповіді, не забуваючи включити відповідну одиницю виміру.

    \(\begin{aligned} SA&=12+120 \\ SA&=132\text{ cm}^{2}\end{aligned}\)

    Відповідь - площа поверхні подарунка Макс купив для своєї мами, становить 132 квадратних сантиметра.

    Приклад\(\PageIndex{1}\)

    Обчисліть площу поверхні наступної трикутної призми:

    Рішення

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=4(6)+(4+7+7)(12)\end{aligned}\)

    Далі помножте базову висоту на площу трикутників (bh) і додайте три сторони трикутника (\(s_{1} + s_{2} + s_{3}\)).

    \(SA=24+18(12)\)

    Потім помножте суму сторін трикутника на висоту призми (H) і додайте значення разом для відповіді, переконавшись, що включили відповідну одиницю виміру.

    \(\begin{aligned} SA&=24+216 \\ SA&=240 cm^{2}\end{aligned}\)

    Відповідь - площа поверхні вищезгаданої трикутної призми становить 240 квадратних сантиметрів.

    Приклад\(\PageIndex{1}\)

    Трикутна призма має трикутний кінець з основою 5 дюймів і висотою 4 дюйми. Довжина кожної сторони становить 8 дюймів, а ширина кожної сторони - 6 дюймів. Яка площа поверхні призми?

    Рішення

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=5(4)+(5+6+6)(8)\end{aligned}\)

    Далі множимо підставу на висоту площі трикутників (bh) і складаємо їх три сторони (s_ {1} + s_ {2} + s_ {2} + s_ {3}\)).

    \(SA=20+17(8)\)

    Потім помножте суму сторін трикутника на висоту призми (H) і складіть значення разом для відповіді, не забуваючи включити відповідну одиницю виміру.

    \(\begin{aligned} SA&=20+136 \\ SA&=156\text{ in}^{2}\end{aligned}\)

    Відповідь - площа поверхні вищезгаданої трикутної призми становить 156 квадратних дюймів.

    Приклад\(\PageIndex{1}\)

    Трикутна призма має трикутний кінець з підставою 8 футів і висотою 6 футів. Довжина кожної сторони становить 10 футів, а ширина кожної сторони - 6 футів. Яка площа поверхні призми?

    Рішення

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=8(6)+(8+6+6)(10)\end{aligned}\)

    Далі помножте базову висоту для площі трикутників (bh) та додайте три сторони трикутника (s_ {1} + s_ {2} + s_ {2} + s_ {3}\)).

    \(SA=48+20(10)\)

    Потім помножте суму сторін трикутника на висоту призми (H) і додайте значення разом для відповіді, переконавшись, що включили відповідну одиницю виміру.

    \(\begin{aligned} SA&=48+200 \\ SA&=248\text{ ft}^{2}\end{aligned}\)

    Відповідь - площа поверхні вищезгаданої трикутної призми становить 248 квадратних футів.

    Приклад\(\PageIndex{1}\)

    Трикутна призма має трикутний кінець з основою 12 дюймів і висотою 9 дюймів. Довжина кожної сторони становить 14 дюймів, а ширина кожної сторони - 9 дюймів. Яка площа поверхні призми?

    Рішення

    Спочатку підставляємо задані значення в формулу.

    \(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=12(9)+(9+9+9)(14)\end{aligned}\)

    Далі помножте базову висоту на площу трикутників (bh\)) і додайте три сторони трикутника (\(s_{1} + s_{2} + s_{3}\)).

    \(SA=108+27(14)\)

    Потім помножте суму сторін трикутника на висоту призми (H\)) і складіть значення разом для відповіді, обов'язково включивши відповідну одиницю виміру.

    \(\begin{aligned} SA&=108+378 \\ SA&=486\text{ in}^{2}\end{aligned}\)

    Відповідь - площа поверхні вищезгаданої трикутної призми становить 486 квадратних дюймів.

    Рецензія

    Використовуйте наступний малюнок, щоб відповісти на кожне питання.

    Ф-Д_5Ф53Ф7Д5 CF941F8E3А49CF8А364КС65ФДБ Б 340284287Ф26D8DAB527+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)
    1. Якою одиницею є виміри цієї цифри?
    2. Яка довжина підстави?
    3. Яка ширина підстави?
    4. Яка форма боків?
    5. Яка міра трикутної сторони?
    6. Яка формула знаходження площі поверхні трикутної призми?
    7. Яка площа поверхні цього малюнка?

    Знайдіть площу поверхні кожної трикутної призми.

    1. Трикутна призма має трикутний кінець з основою 4 дюйма і висотою 3 дюйми. Довжина кожної сторони становить 5 дюймів, а ширина кожної сторони - 3 дюйми. Яка площа поверхні призми?
    2. Трикутна призма має трикутний кінець з підставою 4 фути і висотою 5 футів. Довжина кожної сторони становить 6 футів, а ширина кожної сторони - 5 футів. Яка площа поверхні призми?
    3. Трикутна призма має трикутний кінець з основою 3 дюйма і висотою 3 дюйми. Довжина кожної сторони становить 4 дюйми, а ширина кожної сторони - 3 дюйми. Яка площа поверхні призми?
    4. Трикутна призма має трикутний кінець з підставою 6 метрів і висотою 5 метрів. Довжина кожної сторони становить 8 метрів, а ширина кожної сторони - 5 метрів. Яка площа поверхні призми?
    5. Трикутна призма має трикутний кінець з основою 15 футів і висотою 10 футів. Довжина кожної сторони становить 12 футів, а ширина кожної сторони - 10 футів. Яка площа поверхні призми?
    6. Трикутна призма має трикутний кінець з основою 9 дюймів і висотою 7 дюймів. Довжина кожної сторони становить 9 дюймів, а ширина кожної сторони - 7 дюймів. Яка площа поверхні призми?
    7. Трикутна призма має трикутний кінець з основою 8 дюймів і висотою 6 дюймів. Довжина кожної сторони становить 15 дюймів, а ширина кожної сторони - 6 дюймів. Яка площа поверхні призми?
    8. Трикутна призма має трикутний кінець з основою 5,5 футів і висотою 4 фути. Довжина кожної сторони становить 9 футів, а ширина кожної сторони - 5 футів. Яка площа поверхні призми?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.5.

    Ресурси

    Лексика

    Термін Визначення
    Площа Площа - простір в межах периметра двомірної фігури.
    Призма Призма - це тривимірний об'єкт з двома конгруентними паралельними основами, які є багатокутниками.
    Площа поверхні Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта.
    Трикутна призма Трикутна призма - це призма, складена з двох трикутних підстав і трьох прямокутних граней.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Знайдіть площу поверхні відкритого верхнього ящика

    Практика: Площа поверхні призм