9.13: Обсяг призм за допомогою одиничних кубів
- Page ID
- 54509
Використовуйте кубики, щоб знайти обсяг призми.

Завдання Джеррі в його столярному класі - побудувати дерев'яний контейнер для зберігання, який вмістить щонайменше 48 кубічних одиниць матеріалу. Джеррі вже почав на прямокутному контейнері, який має ширину 4 одиниці і 2 одиниці довжини. Джеррі не впевнений, якою висотою повинен бути контейнер, щоб вмістити обсяг 48 кубічних одиниць. Як Джеррі може використовувати цю інформацію для визначення висоти контейнера?
У цьому понятті ви навчитеся визначати обсяг призм за допомогою одиничних кубиків.
Знаходження об'єму призм за допомогою одиничних кубів
Обсяг - це кількість простору всередині суцільної фігури.

Ці кубики складають прямокутну призму. Кубики представляють обсяг призми. Ця призма являє собою п'ять кубиків по два кубики по одному кубу. Іншими словами, це п'ять кубів довжиною, на два куба висотою на один куб шириною. Ви можете помножити кожне з цих значень разом, щоб отримати об'єм прямокутної призми.
\(5\times 2\times 1=10\text{ cubic units }\)
Обсяг прямокутної призми становить 10 кубічних одиниць або\(\text{ units}^{3}\). Одиниці - це кубічні одиниці, тому що ви помножили одиниці 3 рази, коли ви помножили висоту, довжину та ширину.
Ось ще одна призма.
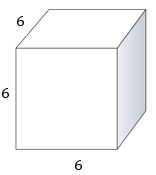
Спочатку, щоб з'ясувати обсяг цієї призми, визначте виміри.
Довжина - 6
Ширина - 6
Висота - 6
Далі підставляємо ці значення в формулу обсягу, потім вирішуємо.
\(\text{Length }\times \text{ Width }\times \text{ Height}=\text{ Volume in cubic units}\)
\(6\times 6\times 6=216\text{ cubic units}\)
Обсяг куба дорівнює\(216\text{ cubic units}\).
Приклад\(\PageIndex{1}\)
Раніше вам дали проблему про Джеррі та контейнері для зберігання, який він будує.
Контейнер має ширину 4 одиниці і 2 одиниці довжини, коли він дізнався про потребу в обсязі. Контейнер повинен мати обсяг 48 кубічних одиниць. Як Джеррі може використовувати цю інформацію для визначення висоти контейнера?
Рішення
По-перше, щоб цифра висоти повинна бути ємність, визначте дані виміри.
Довжина - 2 одиниці
Ширина - 4 одиниці
Висота -?
Обсяг - 48 кубічних одиниць
Далі підставляємо ці значення в формулу обсягу.
\(\begin{aligned} \text{ Length }\times \text{ Width} \times \text{ Height}&=Volume in cubic units \\ 2\times 4\times H&=48 \text{ cubic units}\end{aligned}\)
Потім, розмножуємо.
\(8(H)=48\)
Потім розділіть обидві сторони на 8.
\(H=6\text{ units}\)
Ємність повинна мати висоту 6 одиниць.
Приклад\(\PageIndex{2}\)
Який обсяг у цієї цифри?

Рішення
Спочатку, щоб з'ясувати обсяг цієї призми, визначте виміри.
Довжина - 4 одиниці
Ширина - 4 одиниці
Висота - 3 одиниці
Далі підставляємо ці значення у формулу обсягу, потім вирішуємо.
\(\begin{aligned} \text{ Length}\times \text{ Width}\times \text{ Height}=\text{ Volume in cubic units} \\ 4\times 4\times 3=216 \text{ cubic units}\end{aligned}\)
Обсяг призми дорівнює\(48\text{ cubic units}\), або\(48 \text{ units}^{3}\).
Приклад\(\PageIndex{3}\)
Знайдіть обсяг призми.

Рішення
Спочатку, щоб з'ясувати обсяг цієї призми, визначте виміри.
Довжина - 1
Ширина - 2
Висота - 5
Далі підставляємо ці значення у формулу обсягу, потім вирішуємо.
\(\begin{aligned} \text{Length}\times \text{ Width}\times \text{Height}&=\text{Volume in cubic units} \\ 1\times 2\times 5&=10 \text{ cubic units}\end{aligned}\)
Обсяг призми становить 10 кубічних одиниць.
Приклад\(\PageIndex{4}\)
Знайдіть обсяг призми.
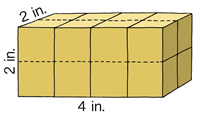
Рішення
Спочатку, щоб з'ясувати обсяг цієї призми, визначте виміри.
Довжина - 2 дюйми
Ширина - 4 дюйми
Висота - 2 дюйми
Далі підставляємо ці значення у формулу обсягу, потім вирішуємо.
\(\begin{aligned} \text{Length}\times \text{Width}\times \text{Height}&=\text{ Volume in cubic units}\\ 2\times 4\times 2&=16 \text{ cubic inches}\end{aligned}\)
Обсяг куба становить 16 кубічних дюймів.
Приклад\(\PageIndex{5}\)
Знайдіть обсяг призми.
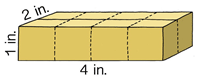
Рішення
Спочатку, щоб з'ясувати обсяг цієї призми, визначте виміри.
Довжина - 2 дюйми
Ширина - 4 дюйми
Висота - 1 дюйм
Далі підставляємо ці значення у формулу обсягу, потім вирішуємо.
\(\begin{aligned} \text{Length}\times \text{Width}\times \text{Height}&=\text{ Volume in cubic units}\\ 2\times 4\times 1&=8 \text{ cubic units}\end{aligned}\)
Обсяг призми становить 8 кубічних дюймів.
Рецензія
Знайдіть обсяг кожної призми.
-
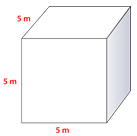
Малюнок\(\PageIndex{8}\) -

Малюнок\(\PageIndex{9}\) -

Малюнок\(\PageIndex{10}\) -
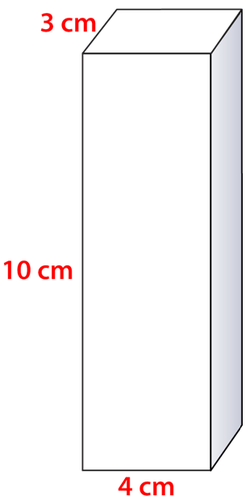
Малюнок\(\PageIndex{11}\) -
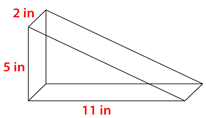
Малюнок\(\PageIndex{12}\) -

Малюнок\(\PageIndex{13}\) -

Малюнок\(\PageIndex{14}\) -

Малюнок\(\PageIndex{15}\) -

Малюнок\(\PageIndex{16}\) -

Малюнок\(\PageIndex{17}\)
Визначте кожен тип призми.
-

Малюнок\(\PageIndex{18}\) -

Малюнок\(\PageIndex{19}\) -

Малюнок\(\PageIndex{20}\) -

Малюнок\(\PageIndex{21}\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.15.
Лексика
| Термін | Визначення |
|---|---|
| Чистий | Сітка - це діаграма, яка показує «сплющений» вигляд твердого тіла. У сітці кожна грань і основа показані з усіма її розмірами. Сітка також може служити візерунком для побудови об'ємного твердого тіла. |
| Прямокутна призма | Прямокутна призма - це призма, складена з двох прямокутних підстав і чотирьох прямокутних граней. |
| Площа поверхні | Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта. |
| Трикутна призма | Трикутна призма - це призма, складена з двох трикутних підстав і трьох прямокутних граней. |
| Обсяг | Об'єм - це кількість простору всередині меж тривимірного об'єкта. |
Додаткові ресурси
Відео: Об'єм твердої геометрії
Практика: Обсяг призм за допомогою одиничних кубів