Skip to main content
LibreTexts - Ukrayinska

9.10: Площа поверхні та об'єм призм

  1. Last updated
  2. Save as PDF
  • Page ID
    54480

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    3-D фігури з 2 конгруентними основами в паралельних площинами і прямокутники для інших їх граней.

    Призми

    Призма - це 3-мірна фігура з 2 конгруентними основами, в паралельних площинях, в яких інші грані є прямокутниками.

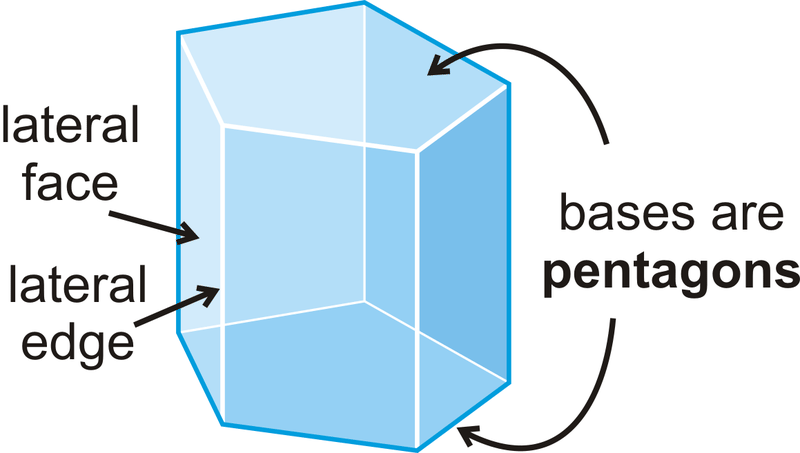
    F-D_4A0C1F7478E56B9F87B4832224A13ce94FCB3B28E71E03124588 АДК+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Небазові грані - це l бічні грані . Краї між бічними гранями - це бічні ребра .

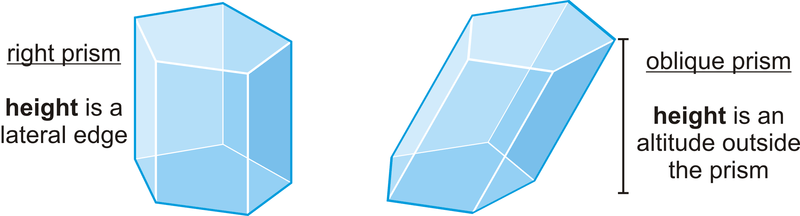
    Цей конкретний приклад є п'ятикутною призмою, оскільки її основою є п'ятикутник. Призми називаються за формою їх підстави. Призми класифікуються як праві призми (призми, де всі бічні грані перпендикулярні основам), або косі призми (призми, що нахиляються в одну сторону, основою якої є паралелограм, а не прямокутник, і висота яких перпендикулярна площині основи), як показано нижче.

    F-д_54Е47 дБ 9СЕ 000Ф821БФ 6А9712Д8 ЕФ3БФКК 971С63ДК1Е37348ЕЕФДК0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Площа поверхні

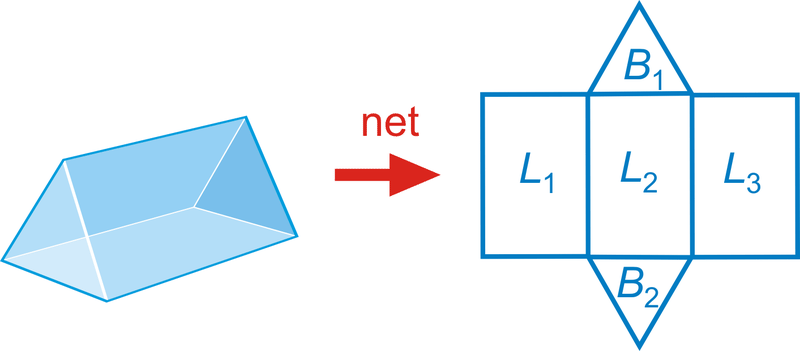
    Щоб знайти площу поверхні призми, знайдіть суму площ її граней. Бічна площа - це сума площ бічних граней. Основною одиницею площі є квадратна одиниця.

    \(Surface Area=B_{1}+B_{2}+L_{1}+L_{2}+L_{3}\)

    \(Lateral Area=L_{1}+L_{2}+L_{3}\)

    F-D_2DE551A9D8043DC6F560 ББК 6ЦБК 94212ce8380BBA00A8367AED CAD5+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Обсяг

    Щоб знайти обсяг будь-якого твердого тіла, ви повинні з'ясувати, скільки місця воно займає. Основною одиницею об'єму є кубічна одиниця.

    Зокрема, для призм, щоб знайти обсяг, ви повинні знайти площу підстави і помножити її на висоту.

    Обсяг призми:\(V=B\cdot h\), де\(B= area\: of\: base\).

    F-д_АФБ 4659a008a536f38655 ФД 9D debcefd94c0b1282c2FDA166672F+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{4}\)

    Якщо коса призма і права призма мають однакову площу підстави і висоту, то вони будуть мати однаковий обсяг. Це пов'язано з принципом Кавальєрі, який стверджує, що якщо два твердих тіла мають однакову висоту і однакову площу поперечного перерізу на кожному рівні, то вони матимуть однаковий обсяг.

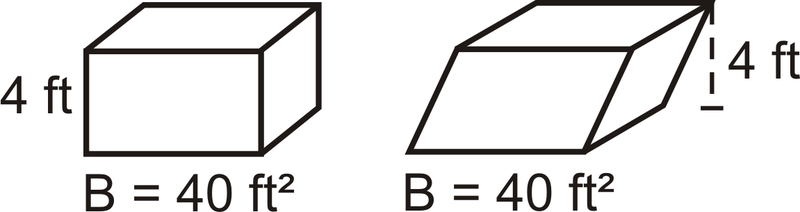
    F-D5AD 76С8С5Д2 АБ 850Б9Ф49 BE97ЕФА08С74А36846FFE3692BB9496D9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Що робити, якщо вам дали суцільну тривимірну фігуру з двома конгруентними основами, в яких інші грані були прямокутниками? Як ви могли визначити, скільки двовимірного та тривимірного простору займає ця фігура?

    Приклад\(\PageIndex{1}\)

    Загальна площа поверхні трикутної призми дорівнює\(540\text{ units}^{2}\). Що таке\(x\)?

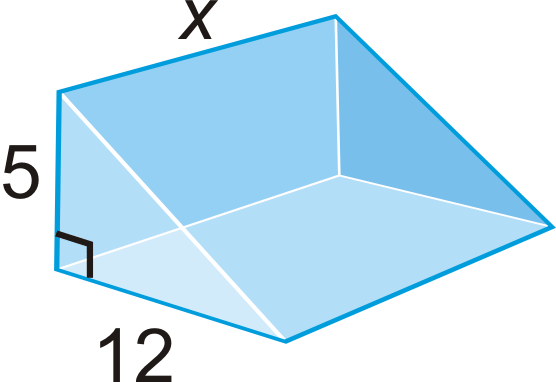
    F-D_0609БД02С6Д7А5С0Д 1973 Б693Ф192Д619А0Б07Е9077C3244812A6B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Загальна площа поверхні дорівнює:

    \(A_{2\: triangles}+A_{3\: rectangles}=540\)

    Гіпотенуза основ трикутника дорівнює 13,\(5^{2}+12^{2}\). Давайте заповнимо те, що ми знаємо.

    F-D_0609БД02С6Д7А5С0Д 1973 Б693Ф192Д619А0Б07Е9077C3244812A6B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    \(\begin{aligned} A_{2\: triangles}=2(\dfrac{1}{2}\cdot 5\cdot 12)=60 \\ A_{3\: rectangles}&=5x+12x+13x=30x \\ 60+30x &=540 \\ 30x&=480 \\ x&=16\text{ units }\qquad \text{ The height is 16 units.}\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Знайдіть обсяг правої прямокутної призми нижче.

    F-д_А947Ф1 ЕАС 6ДК073386967 E23223D654Ф93905А852 ЕКА65Ф9ФБ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Рішення

    Площа\((5)(4)=20\) підстави дорівнює і висоті 3. Отже, загальний обсяг\((20)(3)=60\text{ unit}^{3}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть площу поверхні призми нижче.

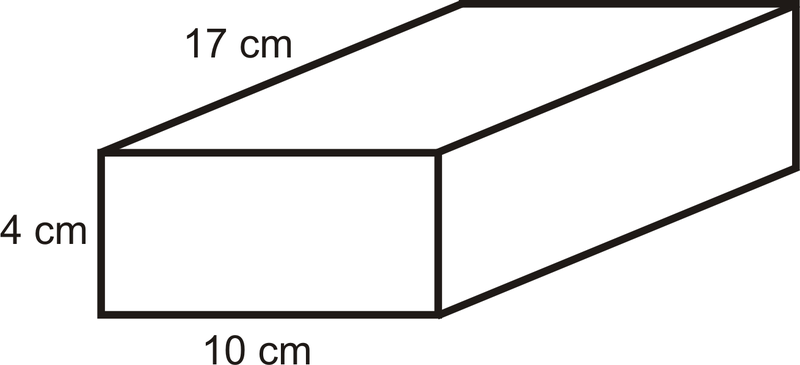
    Ф-Д_БД4 БД4 Б 07С4Е7де 839Е8Ф32А24Д06Ф023КСЕ 46AD063025BDE8A2D46B6B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

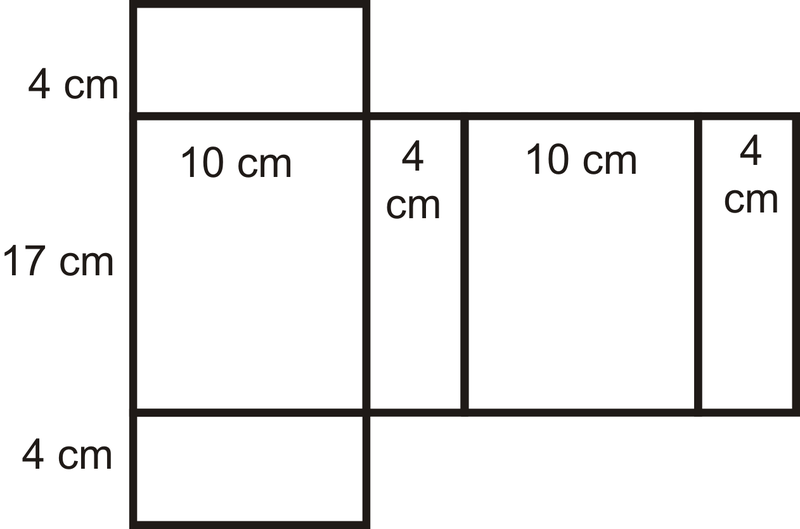
    Щоб вирішити, намалюйте сітку призми, щоб ми могли переконатися, що знайдемо площу ВСІХ граней.

    Використовуючи мережу, ми маємо:

    \(\begin{aligned} SA_{prism}&=2(4)(10)+2(10)(17)+2(17)(4)\\ &=80+340+136 \\ &=556 \text{ cm}^{2}\end{aligned}\)

    F-D_A9 ДД1720А1Е6С4076391С9АБ8С3ФК 2027С931Д2БББ 24Ф6Д4 Бедд+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть площу поверхні призми нижче.

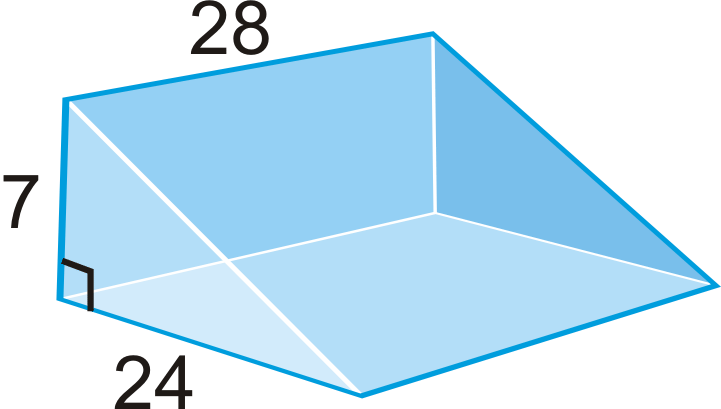
    Ф-д_Б98Ф88А9 ЕБ1150291Е0 Фаб50А5АААААБ 6А4С2ЦЕ90ФББА 1848 CF348ce3+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{11}\)

    Рішення

    Це права трикутна призма. Щоб знайти площу поверхні, нам потрібно знайти довжину гіпотенузи підстави, оскільки це ширина однієї з бічних граней. Ми можемо використовувати теорему Піфагора, щоб знайти цю довжину.

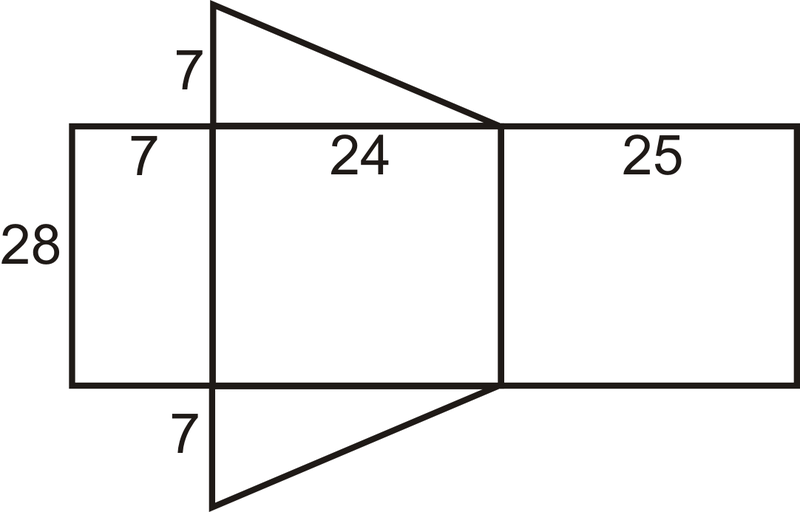
    Ф-д_7Е7612Е8Д622С0АД С4053Ф76Ф2Д91Ф5259ЕФ11981422664C70F5+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{12}\)

    \(\begin{aligned} 7^{2}+24^{2}&=c^{2} \\ 49+576&=c^{2} \\ 625&=c^{2} \qquad c=25\end{aligned}\)

    Дивлячись на сітку, площа поверхні становить:

    \(\begin{aligned} SA&=28(7)+28(24)+28(25)+2(\dfrac{1}{2}\cdot 7\cdot 24) \\ SA&=196+672+700+168=1736 units^{2}\end{aligned}\)

    Приклад\(\PageIndex{5}\)

    У вас невеликий, трикутний намет у формі призми. Скільки гучності він має після того, як він налаштований?

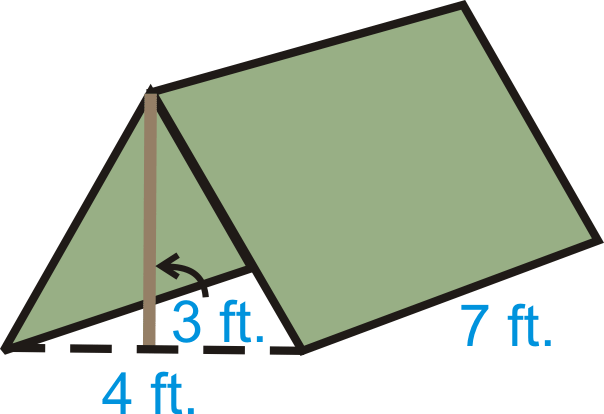
    F-D_5546 ЕФ6ЕД 0Д42А4С78С2953879Д2Д А6С11Ф2Е6ДФ 53109 AFF7D2CC442+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{13}\)

    Рішення

    Для початку нам потрібно знайти площу підстави.

    \(\begin{aligned} B&=\dfrac{1}{2}(3)(4)=6 \text{ ft}^{2} \\ V&=Bh=6(7)=42 \text{ ft}^{3}\end{aligned}\)

    Незважаючи на те, що висота в цій задачі не виглядає як «висота», це тому, що це перпендикулярний відрізок, що з'єднує дві основи.

    Рецензія

    1. Що це за тип призми?
      F-д_70493DA26E6230E6F5E80d1401 КБ БДФ обличчя 4Ф242Ф1ДД21521АФ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
    2. Намалюйте сітку цієї призми.
    3. Знайдіть площу підстав.
    4. Знайдіть площу бічних граней, або площу бічної поверхні.
    5. Знайти загальну площу поверхні призми.
    1. Скільки одиничних кубиків може поміститися в коробку шириною 8 дюймів, довжиною 10 дюймів і 12 дюймів заввишки? Це те саме, що і обсяг коробки?
    2. Зернова коробка шириною 2 дюйми, довжиною 10 дюймів і 14 дюймів заввишки. Скільки крупи вміщує ящик?
    3. Банка соди має висоту 4 дюйми і має діаметр 2 дюйми. Скільки соди тримає балончик? Округлите свою відповідь до найближчої сотої.
    4. Куб тримає\(216\text{ in}^{3}\). Яка довжина кожного краю?
    5. Куб має сторони, які становлять 8 дюймів. Що таке обсяг?

    Використовуйте праву трикутну призму, щоб відповісти на питання 11-15.

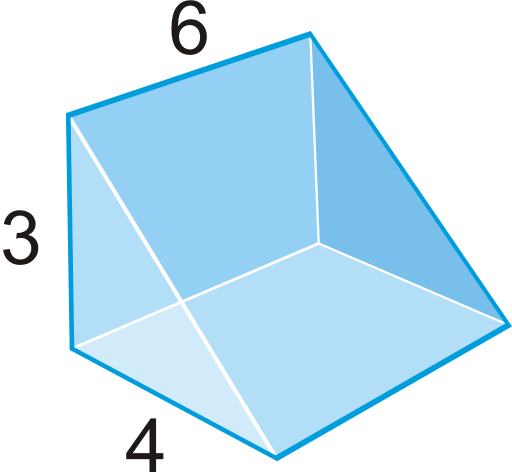
    F-д_Е4628Ф2505А 150238 ССД Ед 7446С4Б68КФА353ДДБ6Б95С7771FE7192+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{15}\)
    1. Знайдіть обсяг призми.
    2. Якої форми мають підстави цієї призми? Які їх області?
    3. Які розміри кожної з бічних граней? Які їх області?
    4. Знайдіть площу бічної поверхні призми.
    5. Знайти загальну площу поверхні призми.
    6. Опишіть різницю між площею бічної поверхні та загальною площею поверхні.
    7. Нечіткі кубики - це кубики з 4-дюймовими сторонами.
      F-D_515D1 ЕАД 40Д672АФ 693537545д175Ф9С6Е473А5Ф3536249561А4+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
      1. Який обсяг і площа поверхні однієї матриці?
      2. Який обсяг і площа поверхні обох кубиків?

    Знайдіть обсяг наступних твердих тіл. Округляйте свої відповіді до найближчих сотих.

    1. підстави - рівнобедрені трапеції
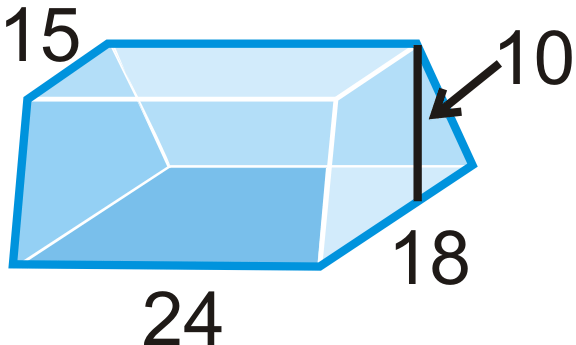
      F-D_111BFA9B0392D585689 ФА8А3296 ЕА ААД 93031ЕА 33696123DB835C6EE+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
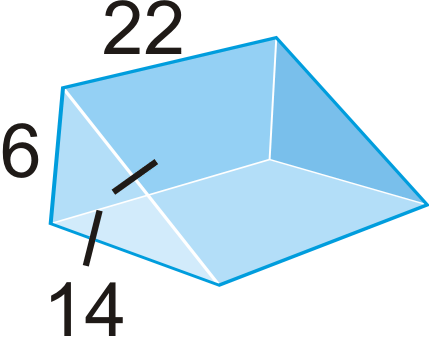
    2. F-D_B6080d961312676 BE4C5F26031Б524С1255ФА42CFF2Б57D627B7AD3E+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
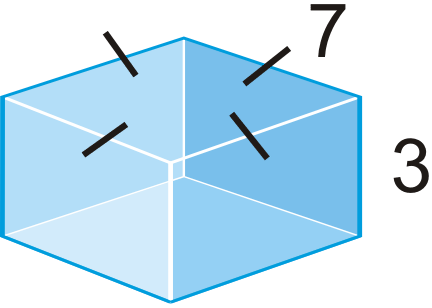
    3. F-д_9692 ЕЦБ 397С5ЕАА9ДБ Б 29Б821д3д7Б636104Б5Е4741Д53+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
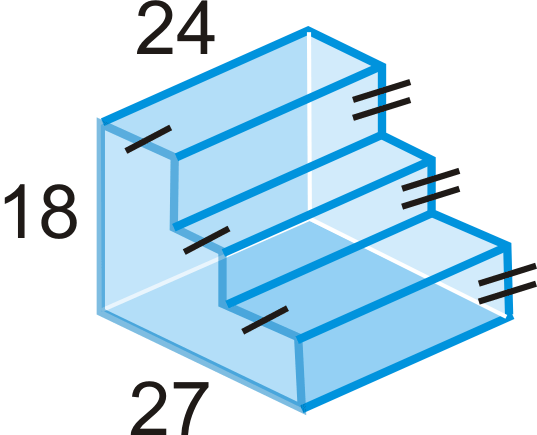
    4. F-D_85F69 CCC685A386FC242 АС 42А445Д3А46С51 ЕАА2А7Б7Д16Б244Д208+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)

    Знайдіть величину\(x\), задану площу поверхні.

    1. \(V=504 \text{ unit}^{3} \)
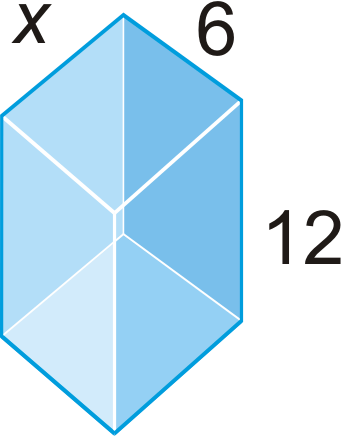
      F-D_527A8D6708A8F6D64А96ФБЦА8ФБКА846ФБ5212Ф30Д584F51E Плата за 04E13C+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)
    2. \(V=2688\text{ unit}^{3} \)
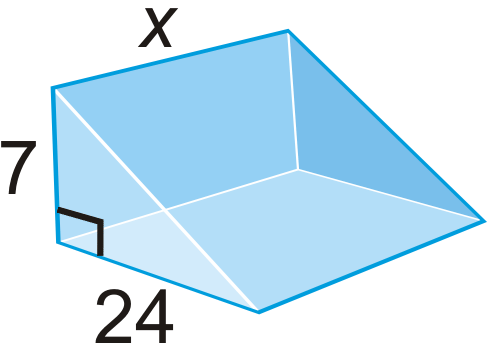
      Ф-д_АД 3Ф9117825Ф2Ф5104Ф2ДА 116585469895698174Б 8А4Д161Ф6С071Ф+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{22}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.3.

    Лексика

    Термін Визначення
    бічні краї Краї між бічними гранями призми.
    коса призма Призма, яка нахиляється в одну сторону і висота якої перпендикулярна площині основи.
    призма являє собою 3-мірну фігуру з 2 конгруентними основами, в паралельних площинам, і в якій інші грані - прямокутники.
    права призма Призма, де всі бічні грані перпендикулярні основам.
    Площа поверхні Площа поверхні - це загальна площа всіх поверхонь тривимірного об'єкта.
    Обсяг Об'єм - це кількість простору всередині меж тривимірного об'єкта.
    Бічні грані Всі грані призми в стороні від основи відомі як бічні грані.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи призми - Основні

    Види діяльності: Призми Дискусійні питання

    Навчальні посібники: посібник з вивчення призм та циліндрів

    Практика: Площа поверхні та об'єм призми