9.9: Застосування площі поверхні та обсягу

Last updated
Save as PDF

Page ID: 54497

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Використовуйте геометричні тіла для моделювання об'єктів реального світу та вирішення проблем. Знайдіть щільність за співвідношенням маси, людей або речей до обсягу або площі.

Моделювання в трьох вимірах

Марк хоче зробити відкриту коробку з аркуша паперу розміром 8,5 дюйма на 11 дюймів, вирізаючи квадрати з кожного кута, склавши боки та закріпивши скотчем. Як обсяг його коробки співвідноситься з розмірами квадратів, які він вирізає?

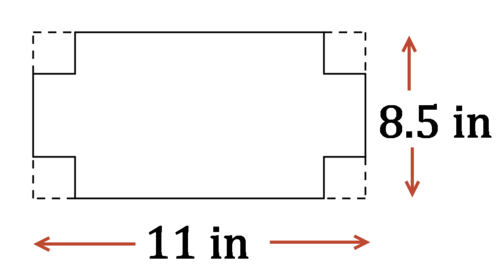
Моделювання в трьох вимірах

Ви живете в тривимірному світі. Озирніться навколо і спостерігайте за тим, що ви бачите протягом дня. Чи можете ви знайти приклади призм? Циліндри? Піраміди? Шишки? Сфери?

Хоча більшість об'єктів у вашому повсякденному житті не є ідеальними призмами, пірамідами, циліндрами, конусами або сферами, більшість з них близькі до однієї з цих п'яти твердих тіл або комбінації цих твердих тіл. Моделювання в трьох вимірах - це можливість вибрати найкраще тверде тіло, щоб допомогти проаналізувати реальну тривимірну ситуацію, а потім використовувати свої знання геометрії для прийняття рішень про реальну життєву ситуацію. Ви повинні запитати себе:

Які тверді або тверді речовини є найкращою моделлю цього об'єкта реального життя?
Які проблеми я намагаюся вирішити або рішення я намагаюся прийняти щодо об'єкта реального життя?
Яку інформацію про об'єкт реального життя я даю і куди вона вписується в мою модель?

Застосування в реальному світі: рубання дерев

Велика буря змушує велике дерево впасти у вашому дворі. Основна частина стовбура дерева має розміри близько 9 футів навколо і має довжину 40 футів. Ви плануєте рубати дерево, щоб використовувати і продавати в якості вогню дрова. Приблизно який обсяг деревини ви отримаєте від дерева?

Стовбур дерева найкраще моделювати циліндром. Тут ви шукаєте приблизний обсяг циліндра. Дві частини інформації наведено.

1. «Основна частина стовбура дерева вимірює близько 9 футів навколо» - Це окружність основи циліндра. Ви можете скористатися цим виміром, щоб знайти радіус циліндра.

$2\pi r=9\rightarrow r=\dfrac{9}{2\pi} \rightarrow r\approx 1.43\text{ ft}$

2. «40 футів завдовжки» - це висота циліндра.

$h=40\text{ ft}$

Обсяг деревини з дерева приблизно дорівнює:

$V=\pi r^{2}h=\pi (1.43^{2})(40)\approx 257\text{ ft}^{3}$

Застосування в реальному світі: Купівля деревини

Деревина зазвичай продається в шнурах. Шнур з дерева - це стопка щільно упакованої деревини, яка вимірює 4 фути на 4 фути на 8 футів. Приблизно скільки шнурів деревини буде виробляти рубане дерево з першої проблеми?

Шнур з дерева найкраще моделювати прямокутної призмою. $V=A_{Base}\cdot h$, Отже$V=(4\cdot 4)\cdot 8=128 ft^{3}$. Кожен шнур деревини становить приблизно 128 кубічних футів деревини. Так як дерево з першої проблеми виробляло 257 кубічних футів деревини, це$\dfrac{257}{128}\approx 2$ шнури з дерева.

Тепер давайте придумаємо рівняння, яке пов'язує довжину навколо дерева в футах, висоту дерева в футах і приблизну кількість шнурів дерева, які дерево буде виробляти.

Ви хочете придумати рівняння, яке приймає вхід окружності та висоти і виробляє вихід шнурів з дерева. Згадайте кроки, зроблені в прикладах A і B, і повторіть ці кроки зі змінними для окружності та висоти замість конкретних значень.

Нехай$C= \text{ distance around the tree}$
Нехай$h= \text{ height of tree}$

Використовуйте відстань навколо дерева, щоб знайти радіус:

$C=2\pi r\rightarrow r=C^2\pi$

Обсяг деревини з дерева становить:

$\begin{aligned} V&=\pi r^{2}h \\ &=\pi (\dfrac{C}{2\pi})^{2}h \\ &=\dfrac{C^{2}h}{4\pi}\end{aligned}$

Після того, як у вас є обсяг деревини з даного дерева, щоб знайти кількість шнурів деревини розділіть обсяг на 128 футів 3, що є кількістю кубічних футів в шнурі дерева.

$\text{Number of Cords}=\dfrac{V}{128}=\dfrac{\dfrac{C^{2}h}{4\pi }}{128}=\dfrac{C^{2}h}{512\pi}$

Перевірте цю формулу, використовуючи оригінальну інформацію з першої проблеми про рубання дерев, щоб побачити, чи отримаєте ви правильну відповідь на другу проблему. У цій першій задачі C = 9 футів і h = 40 футів.

$\text{Number of Cords}=\dfrac{C^{2}h}{512\pi }=\dfrac{(9^{2})(40)}{512\pi }\approx 2.01$

Це відповідає відповіді, тому ви можете бути впевнені, що ваше рівняння правильне.

Приклад$\PageIndex{1}$

Раніше вас запитали, як об'єм коробки Марка співвідноситься з розмірами вирізаних ним квадратів.

Рішення

Нехай довжина сторони квадрата, який Марк вирізає з кожного кута, буде х Частина паперу, яка стане основою коробки, як тільки вона буде зроблена, затінена нижче червоним кольором.

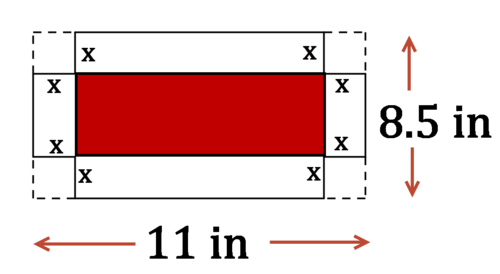
Коробка являє собою прямокутну призму. Тому обсяг коробки дорівнює\ (V=A_ {Base}\ cdot h.

$A_{Base}=(11−2x)(8.5−2x)=4x^{2}−39x+93.5$
$h=x$

Тому обсяг коробки з точки зору розміру квадрата становить:

$V=x(4x2−39x+93.5)=4x^{3}−39x^{2}+93.5x.$

Марку можна за допомогою цієї формули визначити обсяг коробки, враховуючи довжину сторони квадратів, які він вирізає. Наприклад, якщо він вирізає квадрати, які 2 дюйма на 2 дюйма, то х=2. Обсяг коробки становив би:

$V=4(2^{3})−39(2^{2})+93.5(2)=63 in^{3}$

Приклад$\PageIndex{2}$

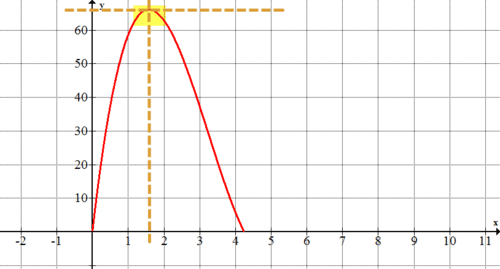
Графік рівняння за$y=4x^{3}−39x^{2}+93.5x$ допомогою графічного калькулятора. Що представляють точки на цьому графіку? Яка частина цього графіка має відношення до цієї проблеми?

Рішення

Точки на графіку представляють обсяг коробки з урахуванням довжини сторони кожного вирізаного квадрата.

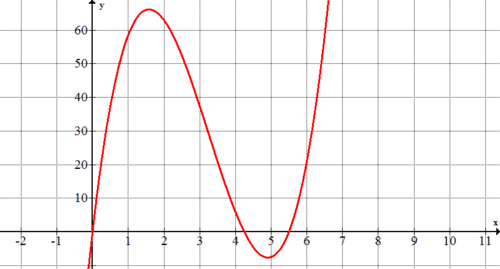
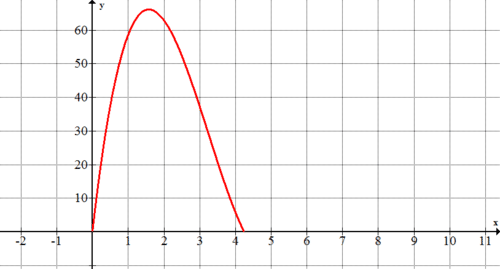
Оскільки Марк не може вирізати квадрат з від'ємною довжиною сторони або квадрат з довжиною сторони більше 4,25 дюйма (оскільки папір має ширину лише 8,5 дюйма), відповідна частина графіка є частиною зі$x$ значеннями від 0 до 4,25.

Приклад$\PageIndex{3}$

Приблизно який розмір квадратів дозволить максимально збільшити обсяг коробки (змусить коробку мати максимально можливий обсяг)? Як графік з #1 допоможе вам відповісти на це питання?

Рішення

Максимальний обсяг, схоже, відбувається з квадратами, які приблизно 1.6 дюйма на 1.6 дюйма. Гучність в цій точці виглядає навколо$66 in^{3}$. Графік допомагає відповісти на це питання, оскільки пік на графіку - це місце, де відбувається максимальний обсяг.

Приклад$\PageIndex{4}$

Чи розмір квадрата, який максимізує об'єм, також максимізує площу поверхні коробки? Поясніть.

Рішення

Площа поверхні відкритого ящика буде площею розгорнутої коробки (сітки). Чим більше ви виріжете з паперу, тим менше площа поверхні. Тому розмір квадрата, який максимізує об'єм, також не максимізує площу поверхні коробки.

Рецензія

Рулон паперових рушників заввишки 11 дюймів має внутрішню картонну трубку діаметром 1,5 дюйма. Ширина паперового рушника на рулоні становить 2 дюйми, а кожен паперовий рушник товщиною 0,015 дюйма.

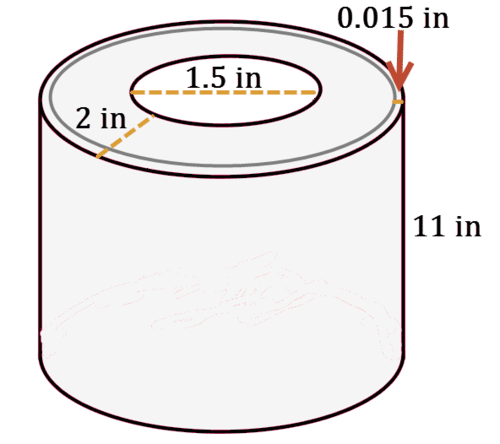
1. Який обсяг паперових рушників? Чи зміниться обсяг, якщо розгорнути рулон паперових рушників?

2. Якщо весь рулон паперових рушників розгортається, як довго буде ланцюжок розгорнутих паперових рушників? [Підказка: Використовуйте свою відповідь на #1, щоб допомогти]

3. Придумайте рівняння, яке узагальнює взаємозв'язок між змінними: діаметр трубки, ширина паперового рушника на рулоні, товщина паперового рушника та довжина розгорнутих паперових рушників. Чому висота рулону паперового рушника не має значення в цих стосунках?

Для того щоб прикрасити торт фіолетовою глазур'ю, Сем планує наповнити глазур'ю мішок сендвіч-блискавки, відрізати один з кінчиків мішка, і видавити глазур з кута (див. Малюнок нижче).

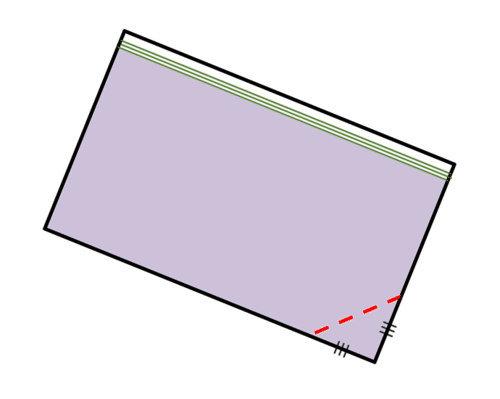
4. Припускаючи, що він вирізає рівнобедрений трикутник з кута, яку довжину зрізу він повинен зробити для обмерзання труби діаметром 1 сантиметр. Іншими словами, якою має бути довжина червоної пунктирної лінії?

5. Дайте рівняння, яке показує залежність між довжиною зробленого розрізу та діаметром глазурі, коли вона виходить з мішка.

6. Ви пакуєте щорічники, які вимірюють 11 дюймів на 14 дюймів на 1,5 дюйма. У вас є коробки, які вимірюють 12 дюймів на 30 дюймів на 10 дюймів. Скільки книг можна помістити в кожну коробку?

Певна палаюча свічка втрачає\ (7 в^ {3} обсягу щогодини.

7. Якщо оригінальна свічка була висотою 10 дюймів при діаметрі 3 дюйми, який обсяг свічки через 3 години?

8. Створіть рівняння, яке пов'язує початкову висоту свічки, діаметр свічки, час горіння та поточний обсяг свічки для всіх свічок, які втрачають$7 in^{3}$ об'єм на годину.

9. Майк і його друзі мають водну повітряну кулю бій. Кожен приблизно сферичний куля вміщує одну чашку води. Якщо одна чашка води має обсяг приблизно$14.44 in^{3}$, який радіус кожного заповненого балона?

Марісса працює в магазині морозива. Цукрові конуси мають діаметр 2 дюйми і висоту 4 дюйми. Для одного конуса совок вона упаковує конус з морозивом, а потім кладе совок зверху. Для подвійного конуса совок вона упаковує конус з морозивом, а потім кладе дві совки зверху (див. Ескіз нижче). Для потрійного конуса совок вона упаковує конус з морозивом, а потім кладе три совки зверху. Одна чашка морозива має обсяг$14.44 in^{3}$.

10. Приблизно скільки морозива (в чашках) отримує один ковшовий конус?

11. Приблизно скільки морозива (в стаканчиках) виходить подвійний конус совок?

12. Приблизно скільки морозива (в стаканчиках) отримує потрійний конус совок?

13. Опишіть принаймні дві причини, чому ваші відповіді на попередні три питання є лише приблизними.

14. Якщо один конус совок коштує $2,50, а подвійний конус совок коштує $3.50. Який тип конуса є кращою угодою, враховуючи вартість за чашку морозива?

15. Якщо один конус совок коштує 2,50 долара, що повинен коштувати потрійний конус совок, якщо він досить цінний?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 9.5.

Лексика

Термін	Визначення
Окружність	Окружність кола - це міра відстані навколо зовнішнього краю кола.

Додаткові ресурси

Практика: Застосування площі поверхні та обсягу