9.8: Площа та об'єм подібних твердих речовин

Last updated
Save as PDF

Page ID: 54453

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Вирішуйте проблеми, використовуючи співвідношення між подібними твердими речовинами.

Зрозумійте відносини масштабу

Тіма має куб з довжиною сторони 4 дюйми. У нього аналогічний куб з розмірами, які вдвічі перевищують перший куб. Як об'єм більшого куба порівнюється з об'ємом меншого куба?

У цій концепції ви навчитеся розуміти масштабні відносини площі та обсягу.

Відносини масштабу

Ви можете порівняти співвідношення масштабу відстані, площі та об'єму при розгляді тривимірних фігур. Деякі приклади тривимірних фігур включають призму або піраміду. Коли ви порівнюєте різні вимірювання, ви побачите пропорційні співвідношення між ними.

Давайте розглянемо ситуацію, пов'язану з обсягом.

Брук має масштабну модель складу. Блок зберігання має форму прямокутної призми і має розміри 4 дюйм. на 3 дюйм. на 6 дюймів. Якщо масштаб моделі є\(0.5 \text{ in}=2\text{ ft}\), які реальні розміри накопичувача? Який обсяг?

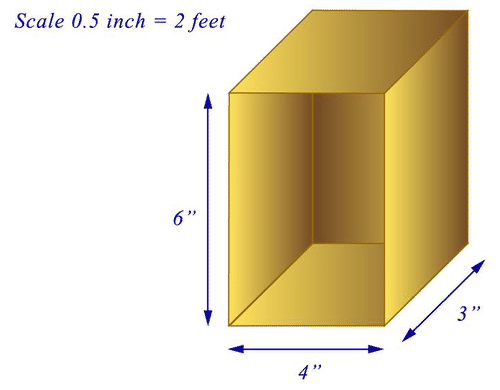
По-перше, зверніть увагу, що є дві частини цієї проблеми. Перша частина - з'ясування фактичних розмірів, враховуючи, що Брук має масштабну модель. Друга частина - з'ясування обсягу. Почніть з використання шкали, щоб написати пропорцію для довжини, ширини та висоти.

\ (\ почати {вирівняний}
&\ текст {довжина}\ квадратний\ текст {ширина}\ квадратний\ текст {висота}\\
&\ frac {0,5\ mathrm {in}} {2\ mathrm {ft}} =\ frac {4\ mathrm {in}} {x\ mathrm {ft}}\ quad\ frac {0.5\ mathrm {2}\ mathrm {ft}} =\ frac {3\ mathrm {in}} {x\ mathrm {ft}}\ квадратний\ frac {0.5\ mathrm {in}} {2\ mathrm {ft}} =\ frac {6\ mathrm {in}} {x\ mathrm {ft}}
\ кінець {вирівняний}\)

Далі перехресне множення для кожного виміру.

\ (\ begin {масив} {ccc}
\ текст {довжина} &\ текст {ширина} &\ текст {висота}\
\ гідророзриву {0.5} {2} =\ frac {4} {x} &\ frac {0.5} {2} =\ frac {3} {x} &\ гідророзриву {0.5} {2} =\ гідророзриву {6} {x}\
0.5 x = 2\ рази 4 & 0,5 х = 2\ раз 3 & 0,5 х = 2\ раз 6\\
0,5 х = 8 & підсилювач; 0,5 х = 6 & 0,5 х = 12
\ кінець {масив}\)

Потім розділіть обидві сторони на 0,5, щоб вирішити для х.

\ (\ begin {масив} {ccc}
\ текст {довжина} &\ текст {ширина} &\ текст {висота}\\
0.5 x=8 & 0.5 x = 6 & 0.5 x = 12
\\\ розриву {0.5} {0.5} =\ розрив {0.5} {0.5 x} {0.5} =\ frac {6} {0.5} &\ frac {0.5 x} {0.5} =\ гідророзриву {12} {0.5}\\
x=16 & x=12 & x=24
\ end {масив}\)

Відповіді 16, 12 і 24.

Довжина одиниці зберігання становить 16 футів, ширина - 12 футів, а висота - 24 фути.

Потім, потрібно розрахувати обсяг накопичувального агрегату.

\(\begin{aligned} V&=l\times w\times h \\ V&=16\times 12\times 24 \\ V&=4608\end{aligned}\)

Відповідь - 4608.

Обсяг одиниці зберігання становить\(4608\: ft^{3}\) або 4608 кубічних футів.

Існує залежність між площею підстави призми і об'ємом призми. Давайте розглянемо, як площа підстави призми відноситься до обсягу призми за допомогою задачі накопичувача.

\(\begin{aligned} A&=l\times w \\ A&=16\times 12 \\ A&=192\end{aligned}\)

Площа призми становить 192 футів ^ {2} або 192 квадратних футів.

Тепер, щоб побачити зв'язок між об'ємом призми і площею призми, розділіть обсяг на площу.

\(\dfrac{V}{A}=4608192\)

\(\dfrac{V}{A}=24\)

Відповідь - 24.

Зверніть увагу, що це висота призми.

Приклад\(\PageIndex{1}\)

Раніше вам давали проблему з приводу кубиків Тіма.

Тім має два кубики, де більший в два рази більше меншого. Це означає, що існує масштабний коефіцієнт 2.

Рішення

Спочатку знайдіть розміри більшого куба.

Менший куб має міру сторони 4 дюйми. Оскільки це куб, довжина = ширина = висота = 4 дюйми.

Більший куб матиме міру сторони 4 в\ разів 2 = 8 дюймів. Тому довжина = ширина = висота = 8 дюймів.

Далі знайдіть обсяг обох кубиків і порівняйте.

\ (\ begin {вирівняний}
&\ текст {Обсяг меншого куба}\ quad\
text {Обсяг більшого куба}\\ &\ begin {масив} {ll}
v=L\ раз h\ times h\\ times h\\
V = 4\ mathrm {in}\ mathrm {in}\ mathrm {in} thrm {in}\ раз 8\ mathrm {in}\ раз 8\ mathrm {in}\\
V = 64\ mathrm {in} ^ {3} & V = 512\ mathrm {in} ^ {3}
\ кінець {масив}
\ кінець {вирівняний}\)

Потім порівняйте обсяг більшого куба з меншим кубом.

\(\begin{aligned} \dfrac{\text{Volume of larger cube}}{\text{Volume of smaller cube}}&=\dfrac{512}{64} \\ \dfrac{\text{Volume of larger cube}}{\text{Volume of smaller cube}}&=8\end{aligned}\)

Відповідь - 8.

Обсяг більшого куба в 8 разів перевищує обсяг меншого куба.

Приклад\(\PageIndex{2}\)

Доведіть, що висоту наступної призми можна знайти, використовуючи відношення обсягу до площі для призми довжиною 6 дюймів, шириною 5 дюймів і висотою 9 дюймів.

Рішення

Спочатку розрахуйте обсяг призми.

\(\begin{aligned} V&=l\times w\times h \\ V&=6\times 5\times 9 \\ V&=270\end{aligned}\)

Далі обчислюємо площу призми.

\(\begin{aligned} A&=l\times w \\ A&=6\times 5 \\ A&=30 \end{aligned}\)

Потім розділіть обсяг на площу.

\(\begin{aligned}\dfrac{V}{A}&=\dfrac{270}{30} \\ \dfrac{V}{A}&=9\end{aligned}\)

Відповідь - 9.

Зверніть увагу, що це висота призми.

Приклад\(\PageIndex{3}\)

Призма має довжину 16 футів, ширину 12 футів і висоту 18 футів. Знайдіть обсяг призми.

Рішення

\(\begin{aligned} V&=l\times w\times h \\ V&=16\times 12\times 18 \\ V&=3456\end{aligned}\)

Відповідь - 3456.

Обсяг призми становить\(3456 ft^{3}\) або 3456 кубічних футів.

Приклад\(\PageIndex{4}\)

Призма має довжину 16 футів, ширину 12 футів і висоту 18 футів. Знайдіть площу підстави.

Рішення

\(\begin{aligned} A&=l\times w \\ A&=16\times 12 \\ A&=192\end{aligned}\)

Відповідь - 192.

Площа призми становить\(192 ft^{2}\) або 192 квадратних футів.

Приклад\(\PageIndex{5}\)

Напишіть співвідношення, порівнюючи обсяг з площею призми і спростіть.

Рішення

\(\beign{aligned}\dfrac{V}{A}&=\dfrac{3456}{192} \\ \dfrac{V}{A}&=18\end{aligned}\)

Відповідь - 18.

Висота призми становить 18 футів.

Рецензія

Вирішіть кожну проблему.

1. Куб вимірює 8 футів з кожного боку. Подібний куб має розміри, які в два рази більше. Як об'єм більшого куба порівнюється з об'ємом меншого куба? Напишіть співвідношення, щоб показати порівняння.

2. Куб вимірює 3 дюйми з кожного боку. Подібний куб має розміри, які вдвічі менше, ніж у іншого куба. Як об'єм більшого куба порівнюється з об'ємом меншого куба? Напишіть співвідношення, щоб показати порівняння

3. Масштабна модель пісочниці має розміри 0,5 дюйма на 3 дюйма на 4 дюйма. Якщо масштаб моделі 1 дюйм = 1 фут, який обсяг фактичної пісочниці?

4. Куб вимірює 5 дюймів з кожного боку. Подібний куб має розміри, які в 3 рази більше. Як об'єм більшого куба порівнюється з об'ємом меншого куба? Напишіть співвідношення, щоб показати порівняння.

5. Коробка для доставки вимірює 16 дюймів на 12 дюймів на 8 дюймів. Друга коробка має аналогічний розмір, але кожен розмір становить 14 як довго. Як обсяг другої коробки порівнюється з обсягом першої коробки?

6. Рибний акваріум Rina має обсяг 8000 кубічних дюймів. Розміри акваріума AVA всі 12 розмір Ріни, Який обсяг акваріума AVA в?

7. Призма має ширину 6 футів, довжину 8 футів і висоту 12 футів. Який обсяг призми?

8. Яка площа підстави цієї призми?

9. Яким був би обсяг призми 14 розміром з описану вище?

10. Яким був би обсяг призми 12 розміром з описану вище?

11. Який об'єм призми був би в два рази більше, ніж описаний вище?

12. Яке співвідношення можна використовувати, щоб виявити взаємозв'язок між об'ємом та площею?

13. Яке вимірювання ви знайдете, спростивши це співвідношення?

14. Правда чи брехня. Ви можете використовувати вимірювання шкали, щоб знайти висоту призми.

15. Правда чи брехня. Ви можете використовувати вимірювання шкали, щоб знайти розміри призми.

Ресурси

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.11.

Лексика

Термін	Визначення
Площа	Площа - простір в межах периметра двомірної фігури.
Масштабна модель	Масштабна модель - це модель, яка представляє тривимірний простір.
Тривимірні	Фігура, намальована в трьох вимірах, малюється з використанням довжини, ширини і висоти або глибини.
Двовимірні	Малюнок, намальований у двох вимірах, малюється лише з використанням довжини та ширини.
Обсяг	Об'єм - це кількість простору всередині меж тривимірного об'єкта.

Відео: Аналогічні принципи твердих тіл - основні

Діяльність: Площа та обсяг подібних твердих речовин обговорення питань

Навчальні посібники: Посібник з вивчення площі поверхні та обсягу

Практика: Площа та об'єм подібних твердих речовин

Реальний світ: Чи є життя там?