9.7: Композитні тверді речовини

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Тверді речовини, що складаються з двох або більше твердих речовин.

Композитний твердий - це тверда речовина, яка складається або складається з двох або більше твердих речовин. Тверді речовини, з яких він складається, як правило, призми, піраміди, конуси, циліндри та сфери. Для того щоб знайти площу поверхні і обсяг складеного твердого тіла, потрібно знати, як знайти площу поверхні і обсяг призм, пірамід, конусів, циліндрів і сфер. Для отримання додаткової інформації про будь-який з цих конкретних твердих речовин зверніться до концепції, яка зосереджена на них. Ця концепція буде припускати знання цих п'яти твердих тіл.

Більшість проблем із композитними твердими речовинами, які ви побачите, стосуватимуться обсягу, тому більшість прикладів та практичних проблем нижче стосуються обсягу. Існує також один приклад площі поверхні.

Що робити, якщо ви побудували цілісну тривимірну модель будинку, що складається з піраміди на вершині квадратної призми? Як ви могли визначити, скільки двовимірного та тривимірного простору займає ця модель?

Приклад $\PageIndex{1}$

Знайдіть обсяг наступного твердого тіла.

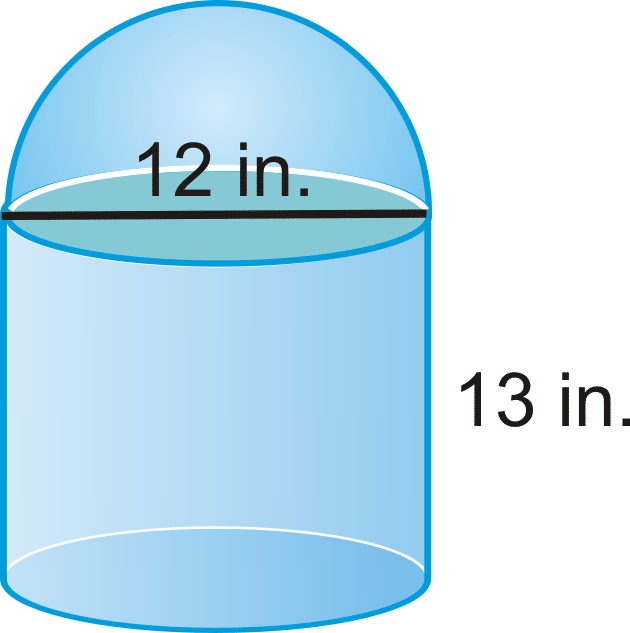
F-D_3002Ф2ДД6285 ЕББ 2А 3А84А18д 375А24Б02А30433 А6 СД 243898Е57+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Рішення

Використовуйте те, що ви знаєте про циліндрах і сферах. Верх твердого тіла являє собою півсферу.

$\begin{aligned} V_{cylinder}&= \pi 6^{2}(13)=468 \pi \\ V_{hemisphere}&=12(\dfrac{4}{3} \pi 6^{3})=144 \pi \\ V_{total}&=468 \pi +144 \pi =612 \pi \text{ in}^{3} \end{aligned}$

Приклад $\PageIndex{2}$

Знайдіть обсяг базової призми. Округлите свою відповідь до найближчої сотої.

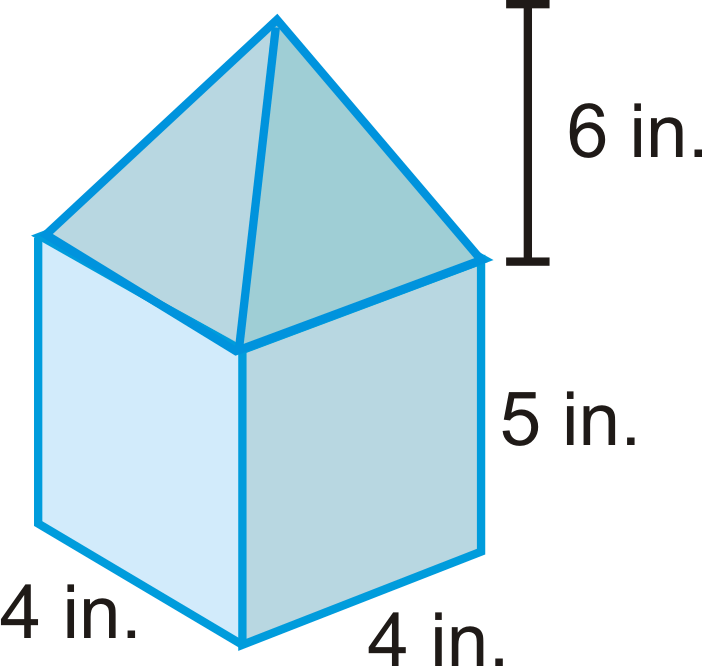
F-D_5610Е76Е1Д109 Каф80ФД6С31А47608ЕЕЕ5БД6БД6С76313809КБ31229+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Рішення

Використовуйте те, що ви знаєте про призми.

$\begin{aligned} V_{prism}=B\cdot h \\ V_{prism}=(4\cdot 4)\cdot 5 \\ V_{prism}=80\text{ in}^{3}\end{aligned}$

Приклад $\PageIndex{3}$

Знайти обсяг твердого тіла нижче.

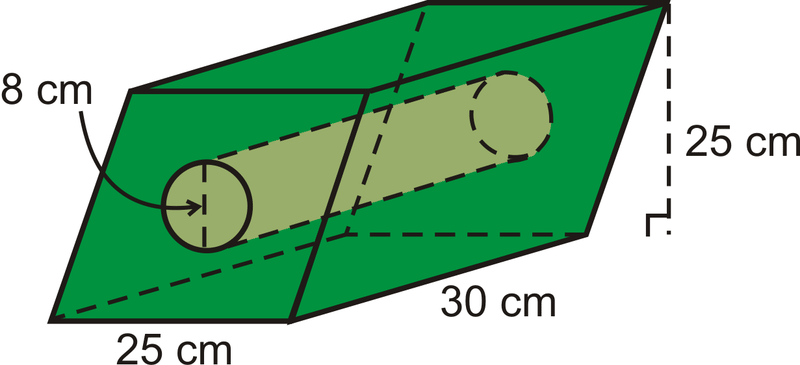
F-Д_8764Д4886731D168БА 27237326420А0Ф231С8725Е009ФД6099ФД 6098799F3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Рішення

Це тверде тіло являє собою призму на основі паралелограма з вирізаним з середини циліндром.

$\begin{aligned} V_{prism}=(25\cdot 25)30=18,750\text{ cm}^{3} \\ V_{cylinder}= \pi (4)^{2}(30)=480 \pi \text{ cm}^{3}\end{aligned}$

Загальний обсяг становить $18750−480 \pi \approx 17,242.04 cm^{3}$ .

Приклад $\PageIndex{4}$

Знайти обсяг складеного твердого тіла. Всі підстави - квадрати.

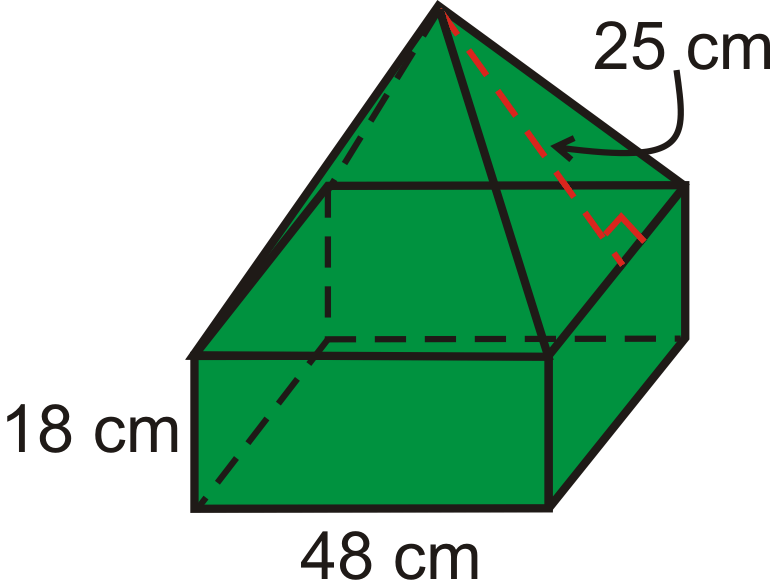
F-D_28A325A534BE28CD80D412E061F073594391d0A0EF2FDC181D6424B9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Рішення

Це квадратна призма з квадратною пірамідою зверху. Для початку нам знадобиться висота піраміди ділянки. Використовуючи теорему Піфагора, ми маємо, $h=\sqrt{25^{2}−24^{2}}=7$ .

$\begin{aligned} V_{prism}&=(48)(48)(18)=41,472\text{ cm}^{3} \\ V_{pyramid}&=\dfrac{1}{3}(48^{2})(7)=5376\text{ cm}^{3}\end{aligned}$

Загальний обсяг становить $41,472+5376=46,848 cm^{3}$ .

Приклад $\PageIndex{5}$

Знайдіть площу поверхні наступного твердого тіла.

Рішення

Це тверде тіло являє собою циліндр з півсферою зверху. Він один суцільний, тому не включайте в себе дно півсфери або верхню частину циліндра.

$\begin{aligned}SA&=LA_{cylinder}+LA_{hemisphere}+A_{base\: circle} \\ &=2 \pi rh+\dfrac{1}{2}4 \pi r^{2}+ \pi r^{2} \\ &=2 \pi (6)(13)+2 \pi 6^{2}+ \pi 6^{2} \\ &=156 \pi +72 \pi +36 \pi \\ &=264 \pi in^{2}\end{aligned}$

«LA» позначає бічну область.

Рецензія

Округляйте свої відповіді до найближчих сотих. Тверда речовина внизу - кубик з вирізаним конусом.

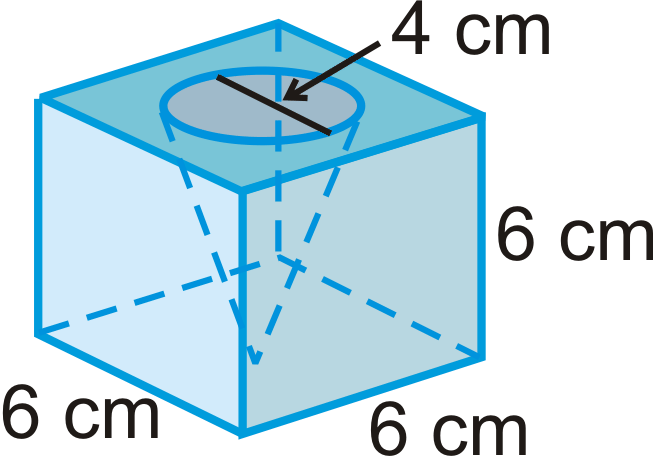
Ф-Д_С4Б87А 8Д950 БЕ17062 А4 АА4 АА32ЕБ ДЕ 1974 Б9Д73Д42Ф1Д3Д1Д11591625Ф4+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Знайдіть обсяг куба.
Знайдіть обсяг конуса.
Знайдіть обсяг всього твердого тіла.

Суцільний внизу - циліндр з конусом зверху.

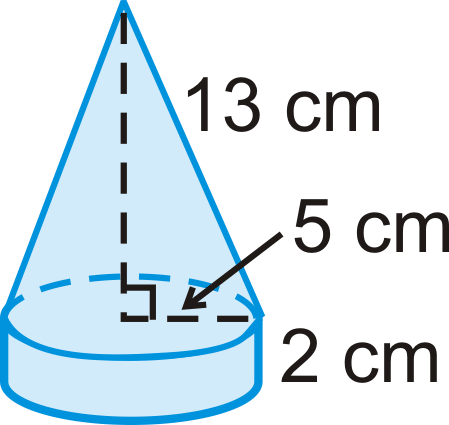
F-д_838Д2С97Б4302Б319А6А84А27800Б5А2775С63Д3Е98Б7410917D23+зображення_крихіткий+зображення_крихіткий_PNG — Малюнок $\PageIndex{7}$

Знайдіть обсяг циліндра.
Знайдіть обсяг конуса.
Знайдіть обсяг всього твердого тіла.

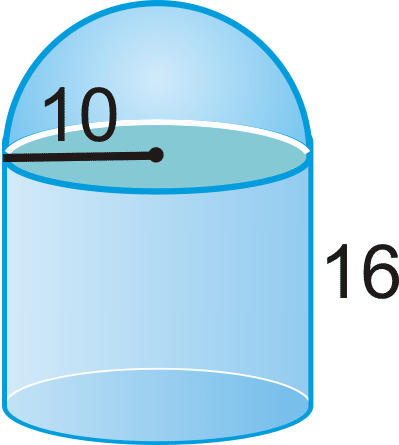
Малюнок $\PageIndex{8}$
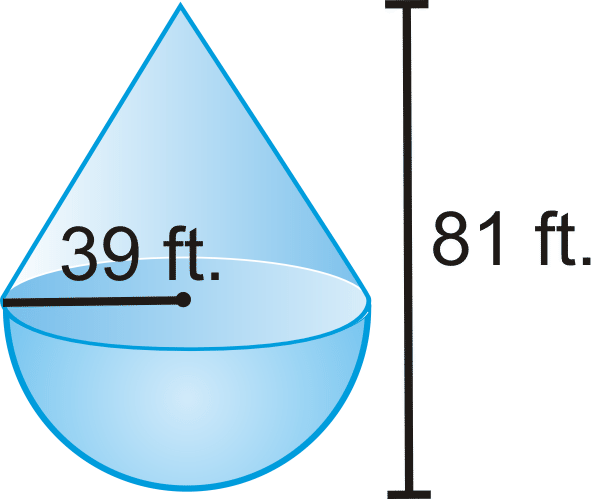
Малюнок $\PageIndex{9}$
Можна припустити, що дно відкрито.

Знайдіть обсяг наступних фігур. Округляйте свої відповіді до найближчих сотих.

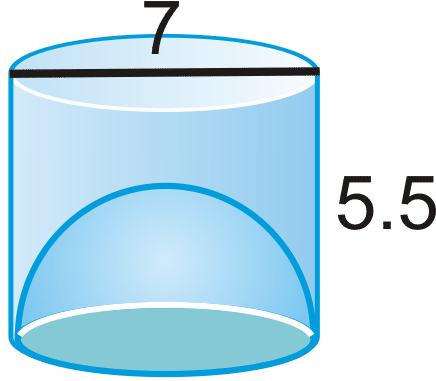
F-д_6С20Ф9 ДБ90560333264А730921Б63Б6Б56К4037ЕФА 8452758Ф CAEF+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{10}$

Малюнок $\PageIndex{11}$
Малюнок $\PageIndex{12}$
Малюнок $\PageIndex{1}$ : Скопіюйте та вставте підпис тут. (Авторське право; автор через джерело)
Сфера має радіус 5 см. Правий циліндр має однаковий радіус і об'єм. Знайдіть висоту циліндра.

Підстави призми - квадрати і з центру вирізається циліндр.

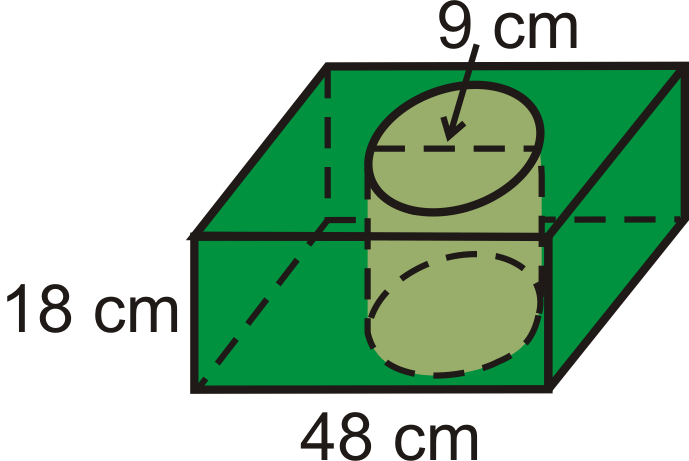F-D_43КББ 494 ФА2СД 8903ЕФ62Ф 65337234ФКБ09Б33361643319E697434+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{13}$

Знайдіть обсяг призми.
Знайдіть обсяг циліндра по центру.
Знайдіть обсяг фігури.

Це призма з половиною циліндра на вершині.

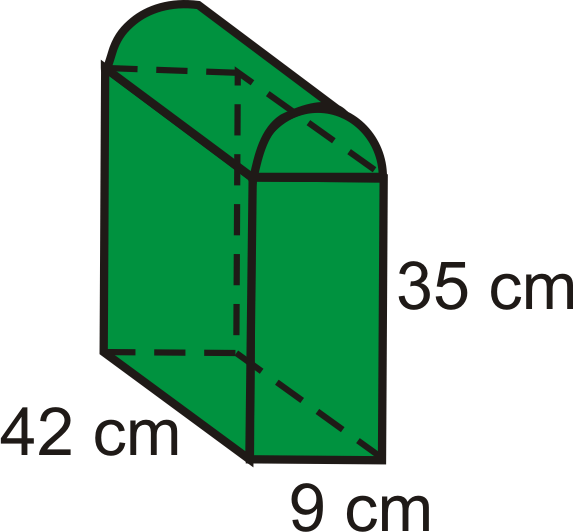F-D_C4 CFC 5Д6Е435Е7Д0456Ф46166Д5С94446270Ф86378Ф43Б1К+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{14}$

Знайдіть обсяг призми.
Знайдіть обсяг півциліндра.
Знайдіть обсяг всієї фігури.

Тенісні м'ячі діаметром 3 дюйма продаються в банках по три. Балончика являє собою циліндр. Округляйте свої відповіді до найближчих сотих.

F-D_CC 08D399228A2A21995B73Da7E46575C921D662EF2E4C07BE06B92392F+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{15}$

Який обсяг одного тенісного м'яча?
Який обсяг циліндра?
Припустимо, що кульки торкаються банки з боків, зверху і знизу. Який обсяг простору, не займаного тенісними м'ячами?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 11.8.

Лексика

Термін	Визначення
композитний твердий	Тверда речовина, яка складається або складається з двох або більше твердих речовин.
обсяг	Тривимірне вимірювання, яке є мірою того, скільки тривимірного простору займає тверде тіло.
Теорема Піфагора	Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана $a^{2}+b^{2}=c^{2}$ , де a і b - катети трикутника, а c - гіпотенуза трикутника.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи композитних твердих тіл - основні

Діяльність: Питання обговорення композитних твердих речовин

Навчальні посібники: Посібник з вивчення площі поверхні та обсягу

Практика: Композитні тверді речовини

Реальний світ: Арки природи