9.5: Обсяг

Кількість одиничних кубів для заповнення призм, сфер, пірамід, циліндрів, конусів та композитних твердих тіл.

Обсяг твердих речовин

Обсяг твердого тіла - це міра того, скільки місця займає об'єкт. Він вимірюється кількістю одиничних кубів, необхідних для заповнення твердого тіла.

Малюнок$\PageIndex{1}$

Обсяг призми

Призма - це суцільне тіло з двома конгруентними основами багатокутників, які паралельні і з'єднані прямокутниками. Призми названі своєю базовою формою.

Малюнок$\PageIndex{2}$

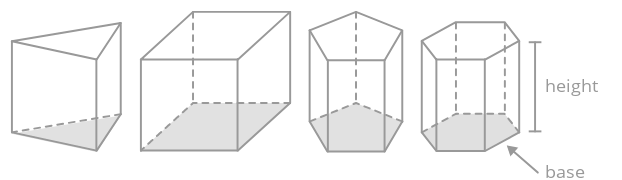
Щоб знайти обсяг призми, знайдіть площу її підстави і помножте на її висоту.
$V_{prism}=A_{base}\cdot h$

Обсяг циліндра

Циліндр являє собою тривимірне тверде тіло, що складається з двох конгруентних, паралельних, круглих сторін (підстав), з'єднаних вигнутою поверхнею.

Малюнок$\PageIndex{3}$

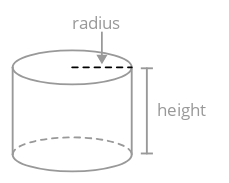
Щоб знайти об'єм циліндра, знайдіть площу його круглої основи і помножте на його висоту.

$V_{cylinder}= \pir^{2}h$

CK-12 PLIX: Площа поверхні та об'єм циліндрів

Інтерактивний елемент

Об'єм піраміди

Піраміда - це тривимірне тверде тіло з багатокутною основою. Кожен кут багатокутника прикріплений до однини вершини, що надає піраміді свою відмінну форму. Кожен базовий край і вершина утворюють трикутник. Піраміди названі за формою основи.

Щоб знайти обсяг піраміди, знайдіть обсяг призми з однаковим підставою і розділіть на три.

Малюнок$\PageIndex{4}$

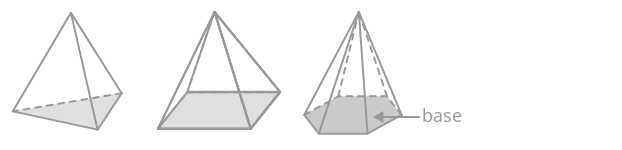
$V_{pyramid}=\dfrac{A_{base}\cdot h}{3}$

Об'єм конуса

Конус являє собою тривимірне тверде тіло з круговою основою, бічна поверхня якого зустрічається в точці, званої вершиною.

Малюнок$\PageIndex{5}$

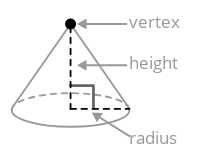
Щоб знайти обсяг конуса, знайдіть обсяг циліндра з однаковим підставою і розділіть на три.

$V_{cone}=\dfrac{ \pi r^{2}h}{3}$

Розглянемо:

Яке співвідношення між об'ємом циліндра і конуса, що мають однаковий радіус і висоту?

Малюнок$\PageIndex{6}$

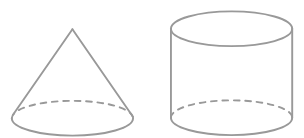
Співвідношення між об'ємом циліндра і конуса з однаковим радіусом і висотою становить _______.

Обсяг сфери

Сфера - це сукупність усіх точок у просторі, рівновіддалених від центральної точки. Відстань від центральної точки до сфери називається радіусом.

Малюнок$\PageIndex{7}$

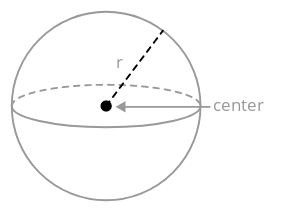
Обсяг сфери спирається на її радіус.

$V_{sphere}=\dfrac{4}{3} \pi r^{3}$

Обчислення обсягу

Клацніть маленьку синю стрілку поруч із зображенням нижче і перетягніть помаранчеві точки, щоб відрегулювати розміри твердого тіла, наведені нижче, і спостерігати за тим, як змінюється гучність.

Малюнок\(\PageIndex{8}\)

Об'єм композитного твердого тіла

Композитне тверде тіло - це тверда речовина, що складається із загальних геометричних твердих тіл. Тверді речовини, з яких він складається, як правило, призми, піраміди, конуси, циліндри та сфери.

Малюнок$\PageIndex{8}$

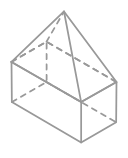
Обсяг композитного твердого тіла - це сума обсягів окремих твердих тіл, що входять до складу композиту.

Давайте розглянемо деякі проблеми, де знаходимо гучність.

1. Знайдіть обсяг прямокутної призми нижче.

Малюнок$\PageIndex{9}$

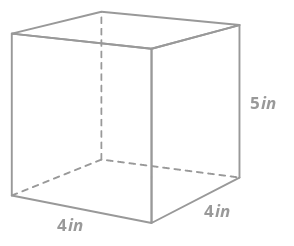
Щоб знайти обсяг призми, потрібно знайти площу підстави і помножити на висоту. Зверніть увагу, що для прямокутної призми будь-яке обличчя може бути «базою», а не тільки особа, яка здається внизу.

Малюнок$\PageIndex{10}$

2. Обсяг конуса знайдіть нижче.

Малюнок$\PageIndex{11}$

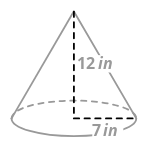
Щоб знайти обсяг конуса, потрібно знайти площу круглої основи, помножити на висоту, і розділити на три.

Малюнок$\PageIndex{12}$

3. Знайдіть обсяг сфери радіусом 4 см.

Малюнок$\PageIndex{11}$

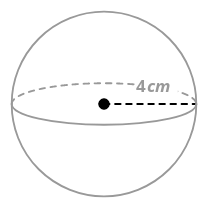
$\begin{aligned} \text{Volume of Sphere }&=&\dfrac{4}{3} \pi r^{3} \\ &=&\dfrac{4}{3} \pi(4)^{3} \\ &=&\dfrac{256 \pi}{3} cm^{3}\end{aligned}$

Приклад$\PageIndex{1}$

Складене тверде тіло внизу виконано з куба і квадратної піраміди. Довжина кожного краю куба становить 12 футів, а загальна висота твердого тіла - 22 фути. Який обсяг твердого тіла? Чому ви можете знати обсяг твердої речовини?

Малюнок$\PageIndex{1}$

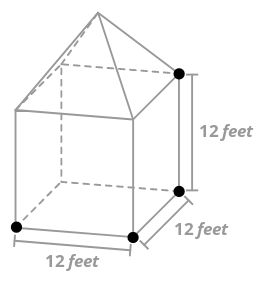
Рішення

Щоб знайти обсяг твердого тіла, знайдіть суму обсягів призми (куба) і піраміди. Зверніть увагу, що оскільки загальна висота становить 22 фути, а висота куба - 12 футів, висота піраміди повинна бути 10 футів.

\ (\ почати {вирівняний}
\ текст {Об'єм призми (куб)} &=A_ {\ текст {база}}\ cdot h\\
& =( 12\ cdot 12) (12)\\
&=1728\ mathrm {ft} ^ {3}\\
\ текст {Обсяг піраміди} &=\ frac {A_ {\ текст {база}}\ cdot {h} 3}\\
&=\ гідророзриву {(12\ точка 12) (10)} {3}\\
&= 480\ mathrm {ft} ^ {3}\\
&=\ текст {обсяг призми (куб)} +\ текст {Обсяг піраміди}\\
&=1728+480\\
&=2208\ mathrm {ft} ^ {3}
\ кінець {вирівняний}\)

Обсяг допомагає дізнатися, скільки буде триматися тверда речовина. Один кубічний фут вміщує близько 7,48 галонів рідини, тому

\ (\ begin {вирівняний}
\ text {Галони рідини, яку може містити тверда речовина} &=\ text {Обсяг твердого тіла. Кількість галонів/кубічних футів}\\
& =( 2208) (7.48)\\
&= 16,515.84\ текст {галони}
\ кінець {вирівняний}\)

Приклад$\PageIndex{2}$

Площа підстави піраміди нижче дорівнює$100 cm^{2}$. Висота - 5 см. Який обсяг піраміди?

Малюнок$\PageIndex{12}$

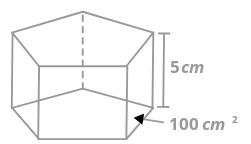
Рішення

$V_{prism}=A_{base}\cdot h=(100\text{ cm}^{2} )\cdot (5 cm)=500\text{ cm}^{3}$

Приклад$\PageIndex{3}$

Обсяг сфери є$\dfrac{500 \pi}{3} in^{3}$. Що таке радіус сфери?

Рішення

Щоб знайти радіус, скористайтеся формулою:$Volume\: of\: Sphere = \dfrac{4}{3} \pir^{3}$

$\begin{aligned} \dfrac{500 \pi}{3}&=\dfrac{4}{3} \pi r^{3} \\ 4r^{3} =500 \\ r^{3} &=125 \\ r&=5\text{ in} \end{aligned}$

Приклад$\PageIndex{4}$

Обсяг квадратної піраміди дорівнює$64 in^{3}$. Висота піраміди в три рази перевищує довжину сторони підстави. Яка висота піраміди?

Рішення

Малюнок$\PageIndex{13}$

Сторона$s=4$ в і висота$h=3(4)=12 in.$

Рецензія

Знайдіть обсяг кожного твердого або композитного твердого тіла.

1. 
   

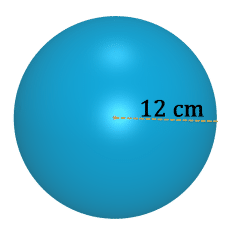
   Малюнок$\PageIndex{14}$

2. 
   

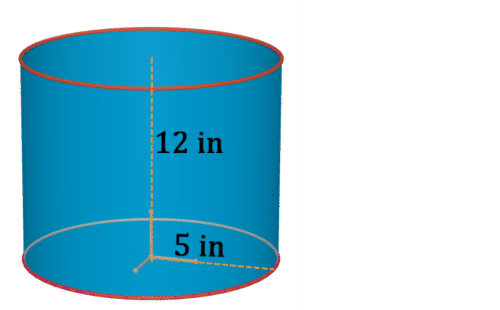
   Малюнок$\PageIndex{15}$

3. 
   

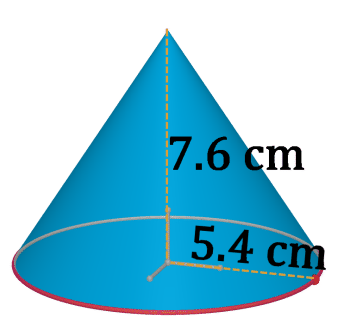
   Малюнок$\PageIndex{16}$

4. 
   

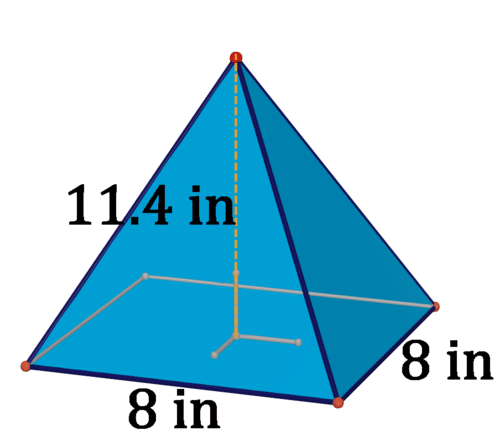
   Малюнок$\PageIndex{17}$

5. Підстава - рівносторонній трикутник.

   
   

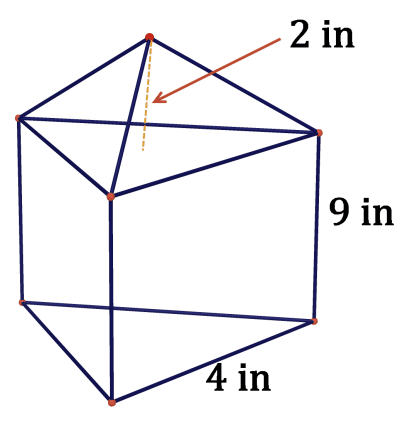
   Малюнок$\PageIndex{18}$

6. 
   

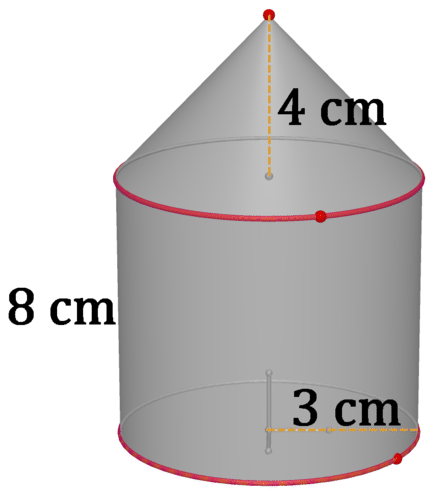
   Малюнок$\PageIndex{19}$

7. Поясніть, чому формула об'єму призми передбачає площу підстави.

8. Як пов'язаний циліндр з призмою?

9. Як пов'язана піраміда з конусом?

10. Як сфера пов'язана з колом?

11. Якщо один кубічний сантиметр вмістить 1 мілілітр води, приблизно скільки літрів води буде тримати тверда речовина в #1? (Один літр - 1000 мілілітрів).

12. Якщо один кубічний сантиметр вмістить 1 мілілітр води, приблизно скільки літрів води буде тримати тверда речовина в #3? (Один літр - 1000 мілілітрів).

13. Якщо 231 кубічних дюймів буде містити один галон води, приблизно скільки галонів води буде тверда речовина в #5 тримати?

14. Обсяг конуса дорівнює$125 \pi in^3$. Висота в три рази перевищує довжину радіуса. Яка висота конуса?

15. Обсяг п'ятикутної призми дорівнює$360 in^3$. Висота призми - 3 дюйми. Яка площа підстави п'ятикутника?

16. На малюнку нижче представлений циліндр, висота якого становить 3 одиниці. Усередині циліндра знаходиться півсфера (половина сфери). А всередині півсфери знаходиться конус. Знайдіть обсяг циліндра і конуса. Знайдіть обсяг сфери, а потім півкулі. Чи бачите ви зв'язок між об'ємом циліндра та конуса та півкулі? Поясніть. Скористайтеся цим, щоб отримати формулу об'єму сфери з формул для циліндра та конуса.

Малюнок$\PageIndex{20}$

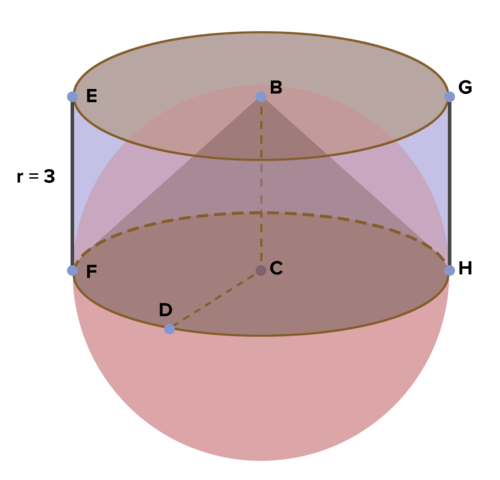
17. Ізометрична сітка нижче складається з рівносторонніх трикутників, сторона яких має одиничну довжину 1. Знайдіть обсяг для кожної з пірамід. Що ви спостерігаєте? Поясніть.

Малюнок$\PageIndex{21}$

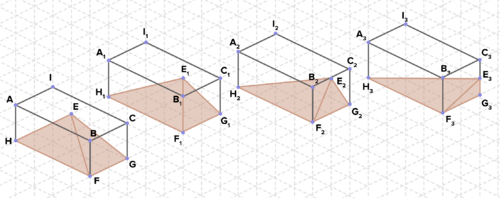
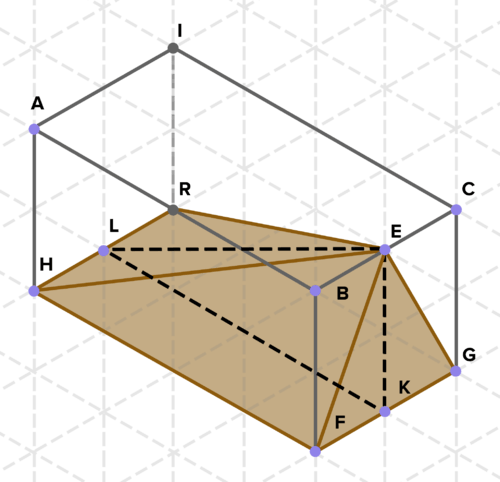
18. Знайдіть площу поверхні і обсяг наступної піраміди. Кожен відрізок лінії у фоновому сітці має довжину 1.

Малюнок$\PageIndex{22}$

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, натисніть тут.