9.4: Площа поверхні

Last updated
Save as PDF

Page ID: 54502

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Площа поверхні та сітки

У геометрії сітка - це 2-мірна форма, яку можна скласти, утворюючи 3-мірну форму або суцільну форму. Або сітка - це малюнок, зроблений, коли поверхня 3-мірної фігури викладається рівно, показуючи кожну грань і край фігури в 2-вимірному вимірі.

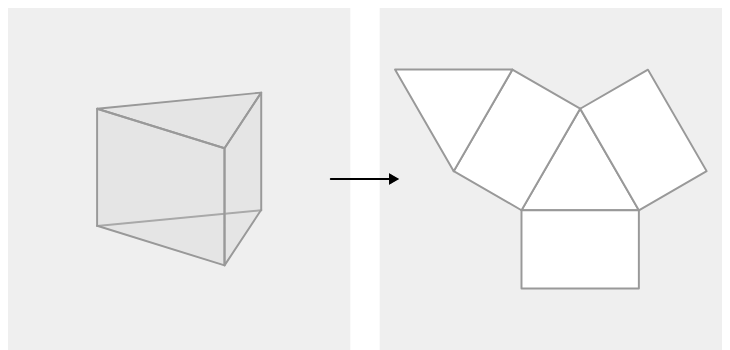
Ось кілька кроків, щоб визначити, чи утворює сітка тверде тіло:

1. Переконайтеся, що тверде тіло і сітка мають однакову кількість граней і що форми граней твердого тіла відповідають формам відповідних граней в мережі.

2. Візуалізуйте, як сітка повинна бути складена, щоб сформувати тверде тіло, і переконайтеся, що всі сторони підходять разом належним чином.

Сітки корисні, коли нам потрібно знайти площу поверхні твердих тіл. На зображенні вище ви можете побачити трикутну призму при розгортанні, що складається з двох трикутників і трьох прямокутників. Трикутники - це основи призми, а прямокутники - бічні грані.

Площа поверхні твердого тіла

Площа поверхні 3-мірного предмета - це міра загальної площі всіх його граней. Це означає, що одним із способів знайти площу поверхні твердого тіла є пошук площі його мережі.

\(Surface\: area\: of\: rectangular\: prism=2ab+2ac+2bc=2(ab+ac+bc)\)

Площа поверхні прямокутної призми - це площа шести прямокутників, які її покривають. Але ми не повинні з'ясовувати всі шість, тому що ми знаємо, що верх і низ однакові, спереду і ззаду однакові, а ліва і права сторони однакові.

Сітки твердих тіл

Дослідіть мережі і подивіться, як 2d фігура перетворюється на 3d фігуру.

Зверніть увагу, що може бути кілька різних інтерпретацій будь-якої мережі. Більшість призм мають кілька сіток.

Інтерактивний елемент

Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах

Знайдіть приблизну площу поверхні трикутної призми нижче. Підстава - рівносторонній трикутник.

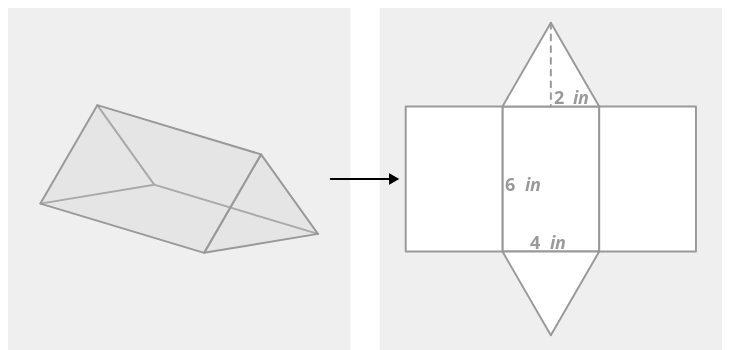
Сітка виконана з трьох конгруентних прямокутників і двох конгруентних рівносторонніх трикутників.

Площа поверхні - це сума площ п'яти фігур. Щоб знайти площу трикутника, потрібно знати висоту трикутника. Використовуючи теорему Піфагора, можна визначити, що висота дорівнює приблизно 3,46 дюйма.

\(H^2=P^2+B^2\)

\(4^2=P^2+2^2\)

\(P^2=16−4=12\)

\(P=3.46 inches\)

Намалюйте сітку квадратної піраміди.

Квадратна піраміда має висоту 20 дюймів. Кожна сторона квадратної основи становить 12 дюймів. Яка площа поверхні піраміди?

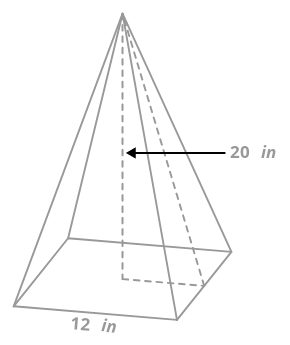
Для того щоб знайти площу поверхні, потрібно визначити площу граней трикутника. Для того щоб знайти площу кожної грані трикутника, вам знадобиться основа і висота трикутника. Для того щоб це зробити, уявіть прямокутний трикутник, що стоїть вертикально в піраміді.

Висота цього трикутника становить 20 дюймів, а основа трикутника - 6 дюймів. Це гіпотенуза, яка є висотою грані трикутника, можна визначити за допомогою теореми Піфагора.

Тепер ви можете знайти площу кожної з п'яти фігур, які складають сітку, щоб знайти площу поверхні.

\(H^2=P^2+B^2\)

\(H^2=20^2+6^2\)

\(H^2=400+36\)

\ (Н=\ квадратний {436} = 20.88 дюймів

Визначте тверде тіло, чиє сітка наведено нижче, виходячи з форми основи.

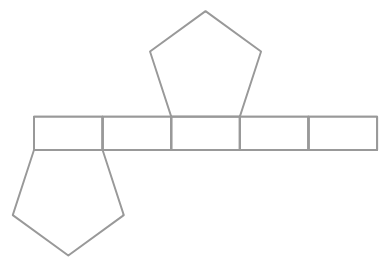
Тверда речовина - _______.

CK-12 PLIX: Поперечні перерізи і сітки

Інтерактивний елемент

Приклад\(\PageIndex{1}\)

Чашка фарби покриває близько 22 квадратних футів. Вам потрібно намалювати всі грані куба, щоб використовувати в якості опори в грі. Кожен край куба має довжину 2,5 футів. Скільки фарби потрібно буде купити?

Рішення

Одна чашка фарби охоплює близько 22 квадратних футів. Кожен край куба має довжину 2,5 футів. Для того щоб розібратися, скільки фарби вам знадобиться, слід знайти площу поверхні куба.

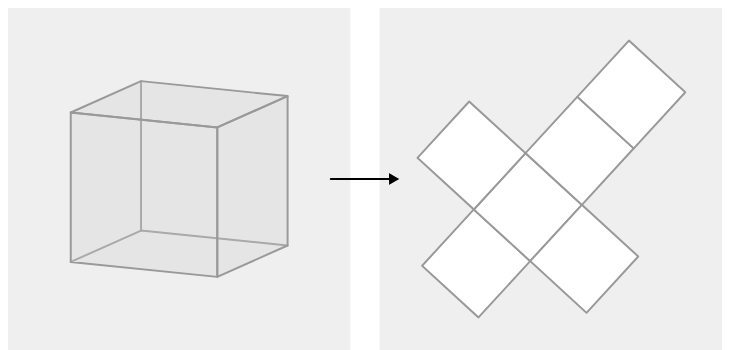
Куб має шість конгруентних квадратних граней. Площа кожного квадрата дорівнює\((2.5)^2=6.25 ft^2\). Загальна площа поверхні куба дорівнює\(37.5 ft^2\). Вам знадобляться\(37.522\approx 1.7\) стаканчики з фарбою.

Приклад\(\PageIndex{2}\)

Намалюйте сітку для п'ятикутної призми.

Рішення

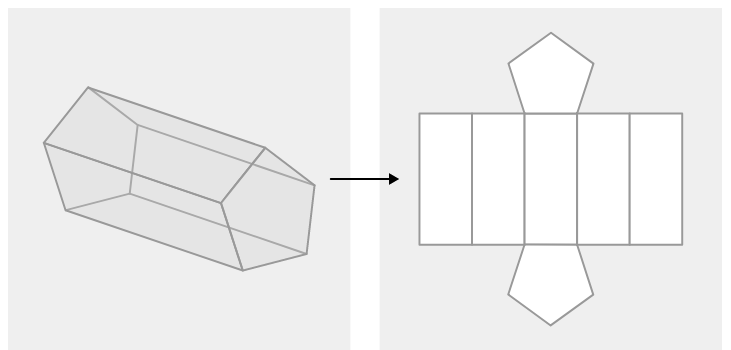
Приклад\(\PageIndex{3}\)

Підставою п'ятикутної призми є наступний п'ятикутник:

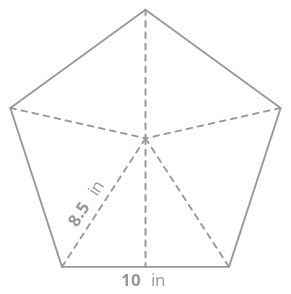
Знайдіть площу п'ятикутника, розсікаючи п'ятикутник на п'ять трикутників і знайшовши площу кожного трикутника.

Рішення

Використовуйте теорему Піфагора, щоб знайти висоту кожного трикутника.

\(H^2=P^2+B^2\)

\(8.5^2=P^2+5^2\)

\(P^2=72.25−25=47.25\)

\(P=\sqrt{47.25}=6.87 inches\)

Приклад\(\PageIndex{4}\)

Знайдіть площу поверхні п'ятикутної призми висотою 25 дюймів і основою, наведеною в прикладі 3.

Рішення

П'ятикутна призма виконана з п'яти прямокутних граней і двох п'ятикутних граней. Кожен прямокутник 10 дюймів на 25 дюймів.

Рецензія

1. Поясніть зв'язок між площею поверхні твердого тіла і сіткою твердого тіла.

2. Коли ви вказуєте площу поверхні, чому ви використовуєте квадратні одиниці, такі як "\(in^2\)«?

Трикутна піраміда має чотири конгруентні рівносторонні грані трикутника. Кожен край піраміди становить 6 дюймів.

3. Намалюйте сітку для піраміди.

4. Знайдіть площу грані одного трикутника.

5. Знайдіть площу поверхні піраміди.

Шестикутна піраміда висотою 20 дюймів має звичайну шестигранну основу, яку можна розділити на шість рівносторонніх трикутників з довжиною сторін 12 дюймів, як показано нижче.

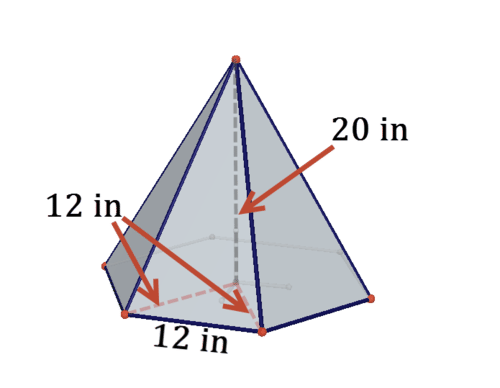
6. Намалюйте сітку для піраміди.

7. Знайдіть площу підстави шестикутника.

8. Піраміда має 6 трикутних граней. Використовуйте теорему Піфагора, щоб допомогти вам знайти висоту кожного з цих трикутників.

9. Знайдіть загальну площу поверхні піраміди.

Квадратна призма увінчана квадратною пірамідою для створення композитного твердого тіла внизу.

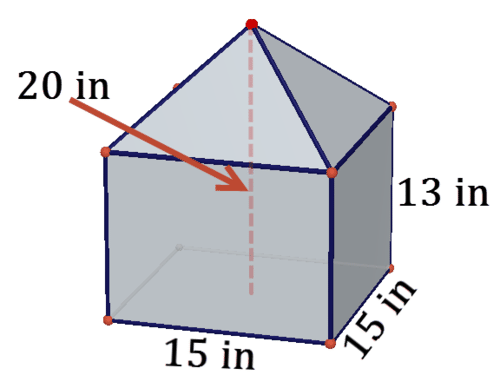
10. Намалюйте сітку для твердого тіла.

11. Є чотири трикутні грані. Використовуйте теорему Піфагора, щоб допомогти вам знайти висоту кожного з цих трикутників.

12. Знайти загальну площу поверхні твердого тіла.

Тверда речовина має наступну сітку.

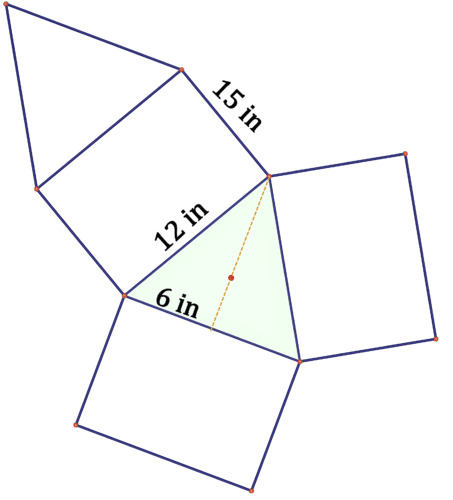
13. Що це за тип твердого тіла?

14. Знайдіть площу поверхні твердого тіла.

15. Як виглядала б сітка циліндра? Спробуйте зробити ескіз.

16. Як би виглядала сітка конуса? Спробуйте зробити ескіз.

16. Графік точок\((2,3)\) і\((12,3)\). Позначте їх A і B і з'єднайте їх, щоб утворити відрізок. Намалюйте вертикальні відрізки, що з'єднують їх з\(x\) віссю. Поверніть цю фігуру навколо\(x\) -осі, щоб сформувати тверде тіло. Яку цифру ви зробили? Поясніть. Знайдіть площу поверхні і обсяг цієї фігури.

17. Графік точок\((2,0)\) і\((10,6)\). Позначте їх A і B і з'єднайте їх, щоб утворити відрізок. Намалюйте вертикальний відрізок від B до\(x\) -осі. Поверніть цю фігуру навколо\(x\) -осі, щоб сформувати тверде тіло. Яку цифру ви зробили? Поясніть. Знайдіть площу поверхні і обсяг цієї фігури.

18. Графік точок\((24,10)\) і\((12,5)\). Сформуйте тверду речовину обороту, як описано вище. Знайдіть його площу поверхні і обсяг.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.11.

Додаткові ресурси

Інтерактивний елемент

Практика: Площа поверхні