Skip to main content
LibreTexts - Ukrayinska

5.28: Зовнішні кути в опуклих багатокутників

  1. Last updated
  2. Save as PDF
  • Page ID
    54851

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Вимірювання кутів на зовнішній стороні багатокутника, утвореного продовженням сторони.

    Теорема про суму зовнішнього кута

    Зовнішній кут - це кут, який утворюється шляхом розширення сторони багатокутника.

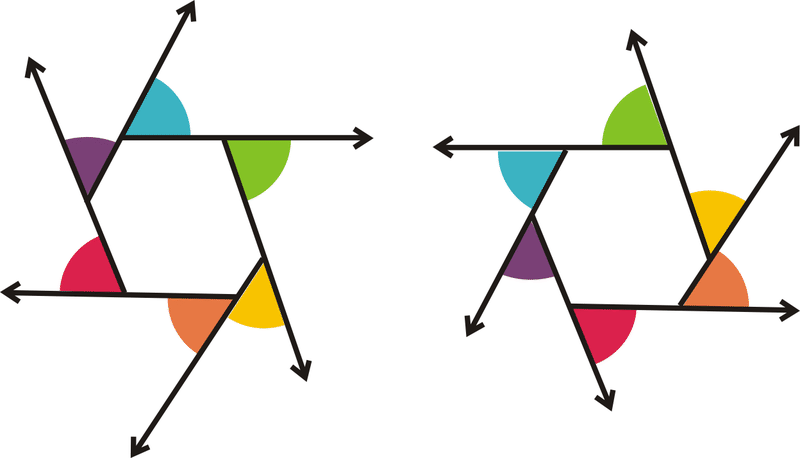
    F-д_93c55f216c91786218045f3400bcd8e12ff0fc8874 Fea71333700992+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Як бачите, існує два набори зовнішніх кутів для будь-якої вершини багатокутника, один йде навколо годинникової стрілки (1-й шестикутник), а інший - проти годинникової стрілки (2-й шестикутник). Кути з однаковими кольорами вертикальні і конгруентні.

    Теорема про суму зовнішнього кута стверджує, що сума зовнішніх кутів БУДЬ-ЯКОГО опуклого багатокутника дорівнює\(360^{\circ}\). Якщо багатокутник правильний з n сторонами, це означає, що кожен зовнішній кут є\(\dfrac{360^{\circ}}{n}\).

    Що робити, якщо вам дали семисторонній правильний багатокутник? Як ви могли визначити міру кожного з його зовнішніх кутів?

    Приклад\(\PageIndex{1}\)

    Яка міра кожного зовнішнього кута правильного 12-кутника?

    Рішення

    \(360^{\circ}\)Ділимо на задану кількість сторін.

    \(30^{\circ}\)

    Приклад\(\PageIndex{2}\)

    Яка міра кожного зовнішнього кута звичайного 100-кутника?

    Рішення

    \(360^{\circ}\)Ділимо на задану кількість сторін.

    \(3.6^{\circ}\)

    Приклад\(\PageIndex{3}\)

    Що таке у?

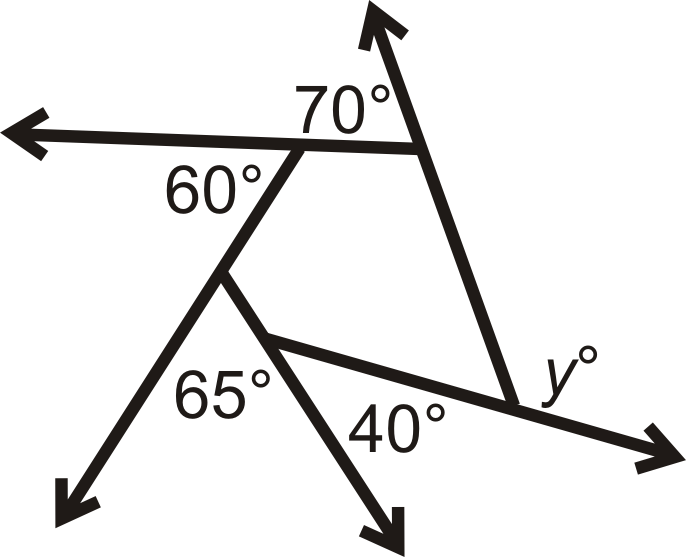
    Ф-д_АА 7748309 ЕББ 648Д121733Е41 СА0653 ДК 76Б0Ф6ФБФ 857960E96912AE+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{2}\)

    Рішення

    \(y\)це зовнішній кут, і всі задані кути складають до\(360^{\circ}\). Налаштуйте рівняння.

    \(\begin{aligned} 70^{\circ}+60^{\circ}+65^{\circ}+40^{\circ}+y&=360^{\circ} \\ y&=125^{\circ} \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Яка міра кожного зовнішнього кута звичайного гептагону?

    Рішення

    Оскільки багатокутник правильний, внутрішні кути рівні. Це також означає, що зовнішні кути рівні. \(\dfrac{360^{\circ}}{7}\approx 51.43^{\circ}\)

    Приклад\(\PageIndex{5}\)

    Яка сума зовнішніх кутів в правильному 15-кутнику?

    Рішення

    Сума зовнішніх кутів у будь-якому опуклому багатокутнику, включаючи правильний 15-кутник, дорівнює\(360^{\circ}\).

    Рецензія

    1. Яка міра кожного зовнішнього кута регулярного декагону?
    2. Яка міра кожного зовнішнього кута правильного 30-кутника?
    3. Яка сума зовнішніх кутів правильного 27-кутника?

    Знайдіть міру відсутніх змінних:

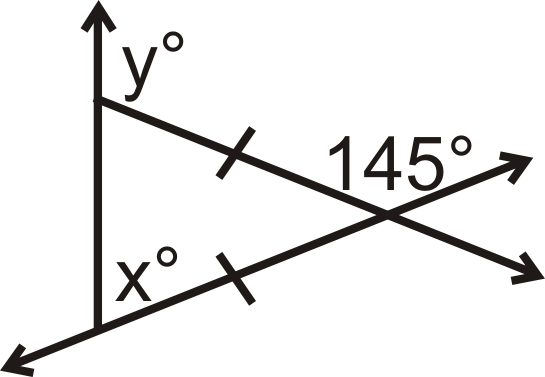
    1. Ф-д_А1152БФ 181 ЕБА 513Д57Б67Д135Ф8Е7С0ДФ339 Ф680Е57Ф42ЕБ7Д0Ф7Д+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{3}\)
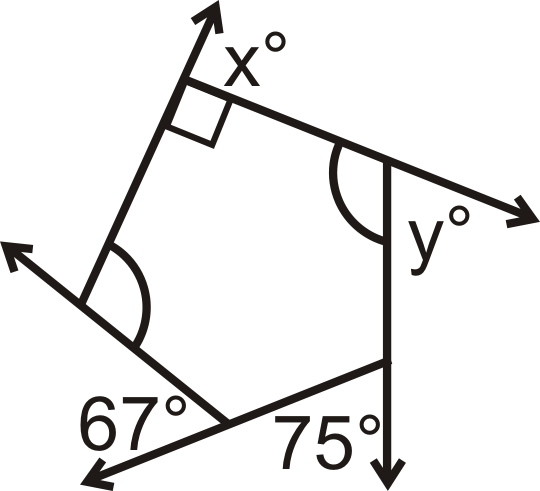
    2. F-д_69769Е9С68321 БК КФ 0AB8080080b54410313CC40 бід 27AEE383BA+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{4}\)
    1. Зовнішні кути чотирикутника є\(x^{\circ}\),\(2x^{\circ}\),\(3x^{\circ}\), і\(4x^{\circ}\). Що таке\(x\)?

    Знайдіть міру кожного зовнішнього кута для кожного правильного багатокутника нижче:

    1. восьмикутник
    2. нонагон
    3. трикутник
    4. п'ятикутник

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.2.

    Ресурси

    Лексика

    Термін Визначення
    зовнішній кут Кут, який утворюється шляхом розширення сторони багатокутника.
    правильний багатокутник Багатокутник, в якому всі його сторони та всі його кути є конгруентними.
    Теорема про суму зовнішнього кута Теорема про зовнішню кутову суму стверджує, що зовнішні кути будь-якого багатокутника завжди додаватимуться до 360 градусів.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Внутрішні та зовнішні кути багатокутника

    Діяльність: Зовнішні кути в опуклих багатокутниках Питання обговорення

    Навчальні посібники: Полігони Навчальний посібник

    Реальний світ: Теорема про зовнішні кути