Skip to main content
LibreTexts - Ukrayinska

5.27: Внутрішні кути в опуклих багатокутників

  1. Last updated
  2. Save as PDF
  • Page ID
    54779

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використовуйте формулу\((x - 2)180\), щоб знайти суму внутрішніх кутів будь-якого багатокутника.

    Внутрішній кут багатокутника - це один з кутів зсередини, як показано на малюнку нижче. Багатокутник має таку ж кількість внутрішніх кутів, як і сторін.

    F-д_389 ФФ0723А 49Е71 Ф9 ЕС7Б5С21806Д212 Бе78А36Е4921973DA5C040+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Сума внутрішніх кутів багатокутника залежить від кількості сторін, які він має. Формула суми багатокутників стверджує, що для будь-якого n−кутника внутрішні кути складаються до\((n−2)\times 180^{\circ}\).

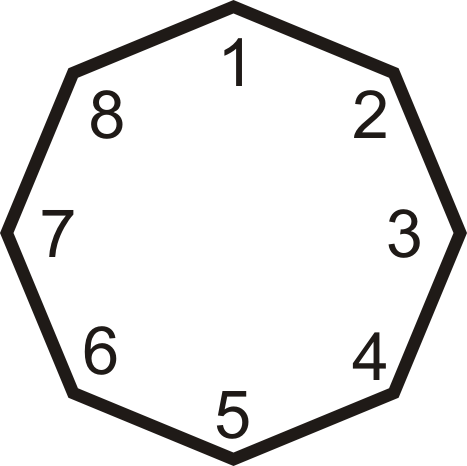
    Ф-Д_ДК 6113С85БФ Ф 0605Б41Б9 А2Е6Ф06809Д9ФК 3633Е6525ФКС7Б83Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    \(\begin{aligned}\rightarrow n=8 \\ (8−2) &\times 180^{\circ} \\ 6 &\times 180^{\circ} \\ &1080^{\circ}\end{aligned}\)

    Після того, як ви знаєте суму внутрішніх кутів у багатокутнику, легко знайти міру ОДНОГО внутрішнього кута, якщо багатокутник правильний: всі сторони конгруентні, а всі кути конгруентні. Просто розділіть суму кутів на кількість сторін.

    Формула внутрішнього кута регулярного багатокутника: Для будь-якого рівнокутного n−кутника мірою кожного кута є\(\dfrac{(n−2)\times 180^{\circ}}{n}\).

    F-D_C35906E4638039AD92C1150CE1C 1Д19012С9780Б4Б8Б1185+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    На малюнку нижче, якщо всі вісім кутів конгруентні, то кожен кут є\(\dfrac{(8−2)\times 180^{\circ}}{8}=\dfrac{6\times 180^{\circ}}{8}=\dfrac{1080^{\circ}}{8}=135^{\circ}\).

    Ф-Д_ДК 6113С85БФ Ф 0605Б41Б9 А2Е6Ф06809Д9ФК 3633Е6525ФКС7Б83Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Що робити, якщо вам дали рівнокутний семисторонній опуклий багатокутник? Як можна було визначити міру його внутрішніх кутів?

    Приклад\(\PageIndex{1}\)

    Внутрішні кути п'ятикутника є\(x^{\circ}\),\(x^{\circ}\),\(2x^{\circ}\),\(2x^{\circ}\), і\(2x^{\circ}\). Що таке\(x\)?

    Рішення

    З формули суми багатокутника ми знаємо, що п'ятикутник має внутрішні кути, які сумуються\((5−2)\times 180^{\circ}=540^{\circ}\).

    Напишіть рівняння і вирішіть для x.

    \(\begin{aligned} x^{\circ}+x^{\circ}+2x^{\circ}+2x^{\circ}+2x^{\circ}&=540^{\circ} \\ 8x&=540 \\ x&=67.5\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Яка сума внутрішніх кутів в 100-кутнику?

    Рішення

    Скористайтеся формулою суми багатокутника. \((100−2)\times 180^{\circ}=17,640^{\circ}\).

    Приклад\(\PageIndex{3}\)

    Внутрішні кути багатокутника складають до\(1980^{\circ}\). Скільки у нього сторін?

    Рішення

    Скористайтеся формулою суми багатокутника і вирішіть для n\).

    \(\begin{aligned} (n−2)\times 180^{\circ}&=1980^{\circ} \\ 180^{\circ}n−360^{\circ}&=1980^{\circ} \\ 180^{\circ}n&=2340^{\circ} \\ n&=13\end{aligned}\)

    Багатокутник має 13 сторін.

    Приклад\(\PageIndex{4}\)

    Скільки градусів має кожен кут у рівнокутному нонагоні?

    Рішення

    Для початку нам потрібно знайти суму внутрішніх кутів; безліч\(n=9\).

    \((9−2)\times 180^{\circ}=7\times 180^{\circ}=1260^{\circ}\)

    «Рівнокутний» говорить нам, що кожен кут дорівнює. Отже, кожен кут є\(\dfrac{1260^{\circ}}{9}=140^{\circ}\).

    Приклад\(\PageIndex{5}\)

    Внутрішній кут у правильному багатокутнику є\(135^{\circ}\). Скільки сторін має цей багатокутник?

    Рішення

    Тут ми встановимо формулу внутрішнього кута регулярного багатокутника рівну\(135^{\circ}\) і вирішимо для n.

    \(\begin{aligned} \dfrac{(n−2)\times 180^{\circ}}{n}&=135^{\circ} \\ 180^{\circ}n−360^{\circ}−360^{\circ}&=135^{\circ}n \\ n&=−45^{\circ} \\ n&=8\qquad \text{The polygon is an octagon.} \end{aligned}\)

    Рецензія

    1. Заповніть таблицю.
    Кількість сторін Сума внутрішніх кутів Вимірювання кожного внутрішнього кута у регулярному n−кутнику
    3 \(60^{\circ}\)
    4 \(360^{\circ}\)
    5 \(540^{\circ}\) \(108^{\circ}\)
    6 \(120^{\circ}\)
    7
    8
    9
    10
    11
    12
    1. Яка сума кутів у 15-кутнику?
    2. Яка сума кутів в 23-кутнику?
    3. Сума внутрішніх кутів багатокутника дорівнює\(4320^{\circ}\). Скільки сторін має багатокутник?
    4. Сума внутрішніх кутів багатокутника дорівнює\(3240^{\circ}\). Скільки сторін має багатокутник?
    5. Яка міра кожного кута в правильному 16-кутнику?
    6. Яка міра кожного кута в рівнокутному 24-кутнику?
    7. Кожен внутрішній кут у правильному багатокутнику є\(156^{\circ}\). Скільки у нього сторін?
    8. Кожен внутрішній кут в рівнокутному багатокутнику є\(90^{\circ}\). Скільки у нього сторін?

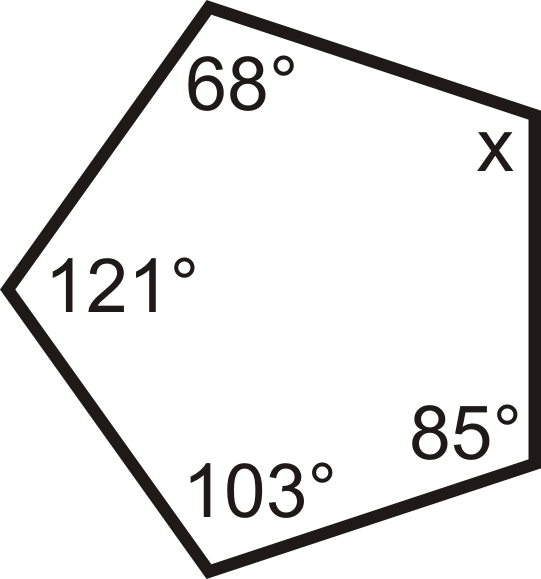
    Для питань 10-18 знайдіть значення відсутньої змінної (ів).

    1. Ф-д_770е735БД ФК 25Ф2205КБ98Б853153С4Д81Б9Ф57С31С62А1БФ1Ф9Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{5}\)
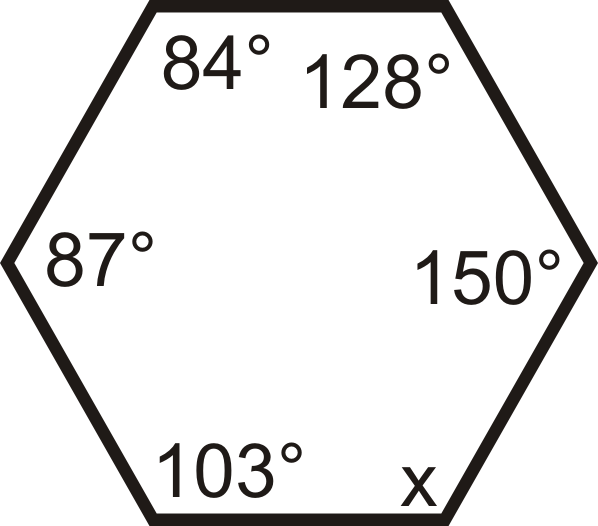
    2. F-д_8Б2Ф07Ф 3979282379916Е 0145А0Д2428 Афе8Е186 ЕЕ7Е4Б69FF9EA+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{6}\)
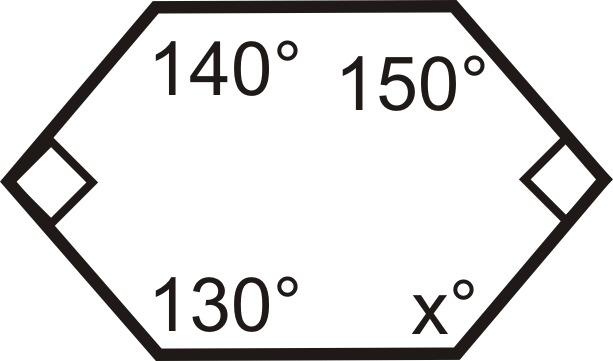
    3. F-д_6Ф05АФ 34Е779ЕЕ6А130Д6 ФБ87ФД1Е3Б6Б6АБ1С562AE758EB3DA37B5+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
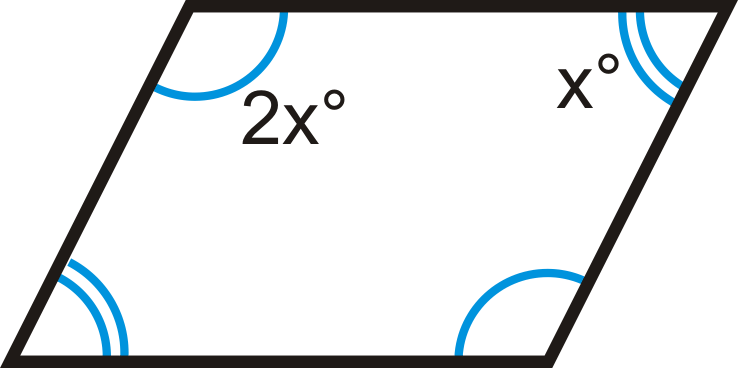
    4. Ф-д_0д617БД2Е1 АА6А844БФ 48С577549 ААА6Ф 6Ф38403000535БФ322А19А09+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
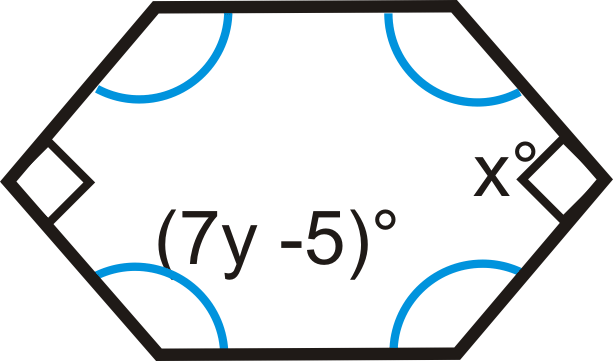
    5. Ф-Д_9 АБ 180Ф78де 27 ДДК 45Ф21657 D68708658 CF13D2CF7F697AD3C840AD+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
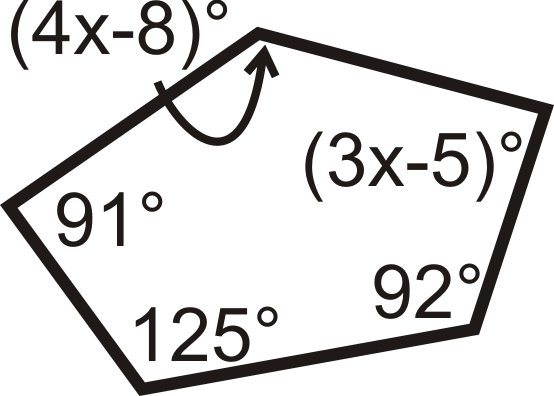
    6. F-D_CB7F7A8 ЕЦФА змінного струму 1С01Ф46Е7Е8ЕФ698986Б1АБД6ДС0Д994CDC3+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
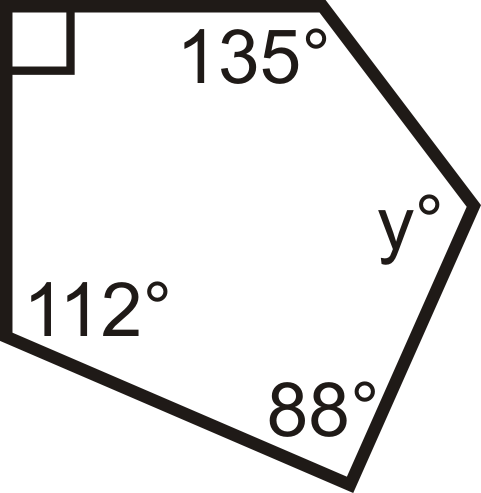
    7. Ф-д_032БФД ББА 1ФКБФ 888838Б594789Ф4Б64423ЕДА 02271С3447D6FB8AE+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
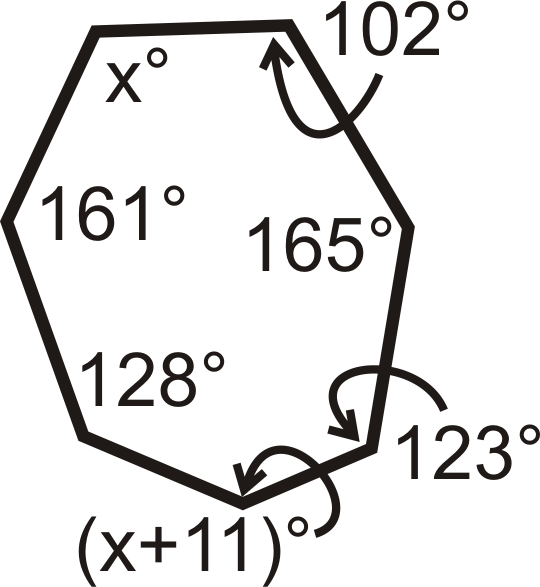
    8. F-д_Д5Б61С48708242ФЕ18АФ6Д0А47Ф368Б 8Д64А857Б80 ЕС2389C57698A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
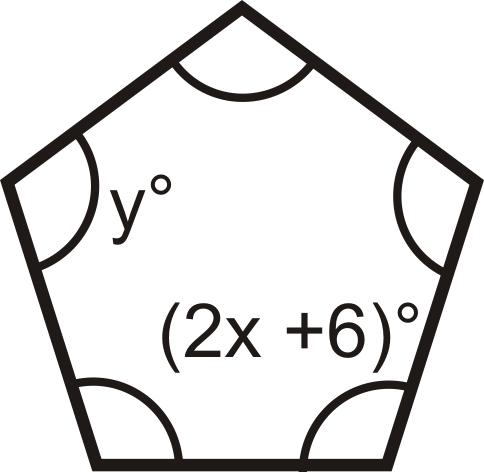
    9. F-д_6 фаа 28д 3С702БД5 АФ5Ф66Д680Д3Ф7164Ф4Ф4А5Б03ФД5Д9990Ф70Б66+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
    1. Внутрішні кути шестикутника є\(x^{\circ}\)\((x+1)^{\circ}\),\((x+2)^{\circ}\),\((x+3)^{\circ}\),\((x+4)^{\circ}\), і\((x+5)^{\circ}\). Що таке\(x\)?

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 6.1.

    Ресурси

    Лексика

    Термін Визначення
    Внутрішні кути Внутрішні кути - це кути всередині фігури.
    Формула суми багатокутника Формула суми багатокутників стверджує, що для будь-якого багатокутника з n сторонами внутрішні кути складаються до\((n−2)\times 180\) градусів.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Внутрішні та зовнішні кути багатокутника

    Діяльність: Внутрішні кути в опуклих багатокутниках Питання обговорення

    Навчальні посібники: Полігони Навчальний посібник

    Практика: Внутрішні кути в опуклих багатокутниках

    Реальний світ: внутрішні кути в опуклих багатокутниках