5.6: Невідомі розміри квадратів і прямокутників

Last updated
Save as PDF

Page ID: 54828

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Обчислити лінійні заходи, задані міри краю або поверхні прямолінійних чотирикутників.

Андреа виходить різдвяні покупки з мамою і плями продажу на різдвяні вогні. Вона запитує свою маму, чи може вона отримати деякі, щоб зав'язати по периметру своєї спальні. Її мама погоджується, тому вони дивляться на пакети, щоб спробувати з'ясувати, скільки їм знадобиться. Мама Андреа не може згадати точні розміри кімнати Андреа, але вона пам'ятає, що це 81 квадратний фут і є квадратом. Як Андреа може зрозуміти, скільки футів різдвяних вогнів їй потрібно?

У цій концепції ви дізнаєтеся, як використовувати формули для вирішення невідомих розмірів при заданому периметрі або площі.

Пошук невідомих розмірів за допомогою формул

Периметр - це відстань навколо фігури. Площа - це кількість квадратних одиниць, що містяться всередині фігури. Периметри і площі прямокутників і квадратів можна знайти, використовуючи наведені нижче формули.

Периметр прямокутника:\(P=2l+2w\)
Квадратний периметр:\(P=4s\)
Площа прямокутника:\(A=lw\)
Площа площі:\(A=s^2\)

Рівняння - це математичне речення, яке говорить про те, що два математичних вирази рівні. Наведені вище формули периметра і площі є прикладами рівнянь. Змінні в цих рівняннях є\(P\)\(A\),\(l\),\(w\),, і\(s\).

Іноді ви будете знати площу або периметр прямокутника або квадрата, але не знаєте інформації про всі його сторони. В цьому випадку ви можете підставити відому інформацію у відповідну формулу і вирішити за невідоме значення. Пам'ятайте, що коли ви вирішуєте рівняння, ви шукаєте значення змінної, яка робить обидві сторони рівняння рівними.

Ось приклад.

Ширина прямокутника становить 10 футів, а периметр - 50 футів. Яка довжина прямокутника?

Для початку розберемося, яка формула актуальна. Це питання про периметр прямокутника, тому ви будете використовувати формулу периметра прямокутника.

\(P=2l+2w\)

Далі з'ясуйте, для яких змінних у вас є значення і для якої змінної ви вирішуєте. Проблема говорить, що ширина 10 футів, тому w=10. Проблема також говорить про те, що периметр становить 50 футів, так що\(P=50\). Ви вирішуєте для довжини.

\( \begin{aligned} P&=50 \\ l&=?\\ w&=10\end{aligned}\)

Тепер підставляємо значення для\(P\) і\(w\) в формулу і спрощуємо.

Далі вирішуємо рівняння. Пам'ятайте, що ви шукаєте значення l, яке зробить обидві сторони рівняння рівними. Спочатку з'ясуйте значення\(2l\) в рівнянні. Задайте собі питання.

«50 дорівнює якому числу плюс 20?»

Потім дайте відповідь на ваше запитання. 30 плюс 20 дорівнює 50, тому\(2l\) має дорівнювати 30.

Тепер у вас є більш просте рівняння для вирішення.

\(2l=30\)

Далі задайте собі інше питання.

«2 рази, яке число дорівнює 30?»

Нарешті, дайте відповідь на ваше запитання. 2 рази 15 дорівнює 30, тому l має дорівнювати 15.

Відповідь полягає в тому, що довжина прямокутника становить 15 футів.

Ви можете перевірити свою відповідь, підставивши всі три значення у формулу периметра прямокутника, оцінюючи та переконавшись, що обидві сторони рівняння дорівнюють один одному.

Відповідь правильна.

Ось ще один приклад.

Якщо площа квадрата становить 144 квадратних миль, яка довжина однієї зі сторін квадрата?

Для початку розберемося, яка формула актуальна. Це питання стосується площі квадрата, тому ви будете використовувати формулу площі квадрата.

\(A=s^2\)

Далі з'ясуйте, для якої змінної у вас є значення і для якої змінної ви вирішуєте. Проблема говорить, що площа 144 квадратних миль, так що A = 144. Ви вирішуєте для довжини боку.

Тепер підставляємо значення A у формулу.

Далі вирішуємо рівняння. Пам'ятайте, що ви шукаєте значення s, яке зробить обидві сторони рівняння рівними. Задайте собі питання.

«144 дорівнює якій кількості разів себе?»

Потім дайте відповідь на ваше запитання. 12 разів 12 дорівнює 144, тому s має дорівнювати 12.

Відповідь полягає в тому, що довжина сторони квадрата становить 12 миль.

Тепер перевірте свою відповідь, підставивши обидва значення у формулу квадратної площі, оцінюючи та переконавшись, що обидві сторони рівняння дорівнюють один одному.

Відповідь правильна.

Приклад\(\PageIndex{1}\)

Раніше вам давали проблему про Андреа та різдвяні вогні.

Вона купує деякі, щоб нанизати по периметру своєї кімнати і повинна знати, скільки футів вогнів купити. Вона знає, що її квадратна кімната має площу 81 квадратних футів.

Рішення

Для початку з'ясуйте довжину кожної сторони її кімнати. Її кімната являє собою квадрат і ви знаєте його площу, тому ви будете використовувати формулу площі квадрата.

\(A=s^2\)

Тепер ви знаєте, що площа площі становить 81 квадратний фут, так\(A=81\). Підставте це значення на A в формулу.

Далі задайте собі питання, яке допоможе вирішити рівняння.

«81 дорівнює якій кількості разів себе?»

Потім дайте відповідь на ваше запитання. 9 разів 9 дорівнює 81, тому s має дорівнювати 9. З кожного боку кімнати Андреа - 9 футів.

Тепер вам потрібно з'ясувати периметр кімнати Андреа, щоб Андреа знав, скільки футів вогнів їй потрібно. Ви знаєте, що кімната являє собою квадрат з довжиною сторони 9 футів. Заставте s=9 у формулу периметра квадрата.

Відповідь полягає в тому, що периметр її кімнати становить 36 футів, тому їй потрібно 36 футів вогнів.

Приклад\(\PageIndex{2}\)

Сім'я Hegazzi розробляє літній сад на основі моделі, показаної нижче. Низ ділянки - квадрат, а верхня частина ділянки - прямокутник. Якщо загальна площа обох ділянок в саду становить 139 квадратних футів, яка довжина однієї сторони квадратної ділянки (вказана знаком питання нижче)?

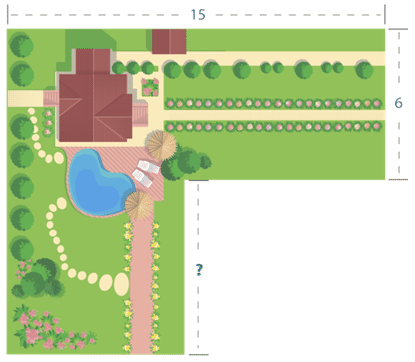
Рішення

Спочатку використовуйте надану інформацію, щоб знайти площу ділянки прямокутника. Потім ви будете використовувати цю інформацію, щоб допомогти вам знайти площу квадратної ділянки, що дозволить вам знайти довжину сторони квадратної ділянки.

Прямокутник має довжину 15 футів і ширину 6 футів. Формула, щоб знайти площу прямокутника, є\(A=lw\). Підставляємо значення довжини і ширини прямокутника в формулу і оцінюємо, щоб знайти площу.

Далі знайдіть площу квадратної ділянки. Ви знаєте, що загальна площа становить 139 квадратних футів, а площа прямокутника - 90 квадратних футів. Ви також знаєте, що загальна площа дорівнює площі прямокутника плюс площа квадрата. Підставте значення, які ви знаєте, в ці відносини.

Тепер вирішіть рівняння, задаючи собі питання.

«139 дорівнює 90 плюс яке число?»

Далі відповімо на питання. 90 плюс 10 дорівнює 100. 100 плюс 39 дорівнює 139. Так 90 плюс 49 повинні дорівнювати 139. Площа квадратної ділянки становить 49 квадратних футів.

Тепер використовуйте площу квадратної ділянки, щоб допомогти вам знайти довжину сторони квадратної ділянки. Підставте значення для\(A\) у формулу площі квадрата.

Далі вирішуємо рівняння.

«49 дорівнює якій кількості разів себе?»

Потім дайте відповідь на ваше запитання. 7 разів 7 дорівнює 49, тому s має дорівнювати 7.

Відповідь полягає в тому, що довжина сторони квадратної ділянки становить 7 футів.

Приклад\(\PageIndex{3}\)

Якщо периметр прямокутника 30 футів, довжина 9 футів, яка ширина прямокутника?

Рішення

\(P=2l+2w\)

Далі з'ясуйте, для яких змінних у вас є значення і для якої змінної ви вирішуєте. Проблема говорить, що периметр 30 футів, тому P = 30\). Проблема також говорить, що довжина становить 9 футів, тому l = 9\). Ви вирішуєте для ширини.

\(\begin{aligned} P&=30 \\ l&=9 \\ w&=? \end{aligned}\)

Тепер підставляємо значення P і l в формулу і спрощуємо.

Далі вирішуємо рівняння. Спочатку з'ясуйте значення\(2w\) в рівнянні. Задайте собі питання.

«30 дорівнює 18 плюс яке число?»

Потім дайте відповідь на ваше запитання. 18 плюс 12 дорівнює 30, тому\(2w\) має дорівнювати 12.

Тепер у вас є більш просте рівняння для вирішення.

\(2w=12\)

Далі задайте собі інше питання.

«2 рази, яке число дорівнює 12?»

Нарешті, дайте відповідь на ваше запитання. 2 рази 6 дорівнює 12, тому w має дорівнювати 6.

Відповідь полягає в тому, що ширина прямокутника становить 6 футів.

Тепер перевірте свою відповідь, підставивши всі три значення у формулу периметра прямокутника, оцінюючи та переконавшись, що обидві сторони рівняння дорівнюють один одному.

Відповідь правильна.

Приклад\(\PageIndex{4}\)

Якщо площа квадрата становить 225 квадратних футів, яка довжина однієї з його сторін?

Рішення

\(A=s^2\)

Далі з'ясуйте, для якої змінної у вас є значення і для якої змінної ви вирішуєте. Проблема говорить, що площа становить 225 квадратних футів, так що\(A=225\). Ви вирішуєте для довжини боку.

Тепер підставляємо значення A у формулу.

Далі вирішите рівняння, задаючи собі питання.

«225 дорівнює якій кількості разів себе?»

Потім дайте відповідь на ваше запитання. 15 разів 15 дорівнює 225, тому s має дорівнювати 15.

Відповідь полягає в тому, що довжина сторони квадрата становить 15 футів.

Відповідь правильна.

Приклад\(\PageIndex{5}\)

Якщо периметр квадрата дорівнює 24 метрам, яка довжина однієї зі сторін?

Рішення

Для початку розберемося, яка формула актуальна. Це питання про периметр квадрата, тому ви будете використовувати формулу периметра квадрата.

\(P=4s\)

Далі з'ясуйте, для якої змінної у вас є значення і для якої змінної ви вирішуєте. Проблема говорить про те, що периметр становить 24 метри, значить\(P=24\). Ви вирішуєте для довжини боку.

Тепер підставляємо значення для\(P\) у формулу.

Далі вирішите рівняння, задаючи собі питання.

«24 дорівнює 4 рази, яке число?»

Потім дайте відповідь на ваше запитання. 4 рази 6 дорівнює 24, тому s має дорівнювати 6.

Відповідь полягає в тому, що довжина сторони квадрата становить 6 метрів.

Тепер перевірте свою відповідь, підставивши обидва значення у формулу квадратного периметра, оцінюючи та переконавшись, що обидві сторони рівняння дорівнюють один одному.

Відповідь правильна.

Рецензія

З огляду на площу, знайдіть довжину сторони для кожного квадрата.

\(A=16\text{ sq. ft. } \)
\(A=64\text{ sq. m. } \)
\(A=100\text{ sq. miles }\)
\(A=121\text{ sq. inches } \)
\(A=144\text{ sq. ft. } \)

З огляду на площу і довжину, знайдіть ширину кожного прямокутника.

\(A=24\text{ sq. feet },\text{ length }=8\text{ feet } \)
\(A=48 \text{ sq. feet },\text{ length }=12\text{ feet } \)
\(A=64\text{ sq. feet },\text{ length }=10\text{ feet } \)
\(A=120\text{ sq. meters },\text{ length }=40\text{ meters } \)
\(A=130\text{ sq. feet },\text{ length }=13\text{ feet } \)
\(A=90\text{ sq. inches },\text{ length }=45\text{ inches } \)

З огляду на периметр, знайдіть довжину сторони кожного квадрата.

\(P=48\text{ inches } \)
\(P=64\text{ inches } \)
\(P=90\text{ inches } \)
\(P=35\text{ feet } \)

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 1.15.

Лексика

Термін	Визначення
Площа	Площа - простір в межах периметра двомірної фігури.
Вимірювання	Вимірювання - це вага, зріст, довжина або розмір чогось.

Додаткові ресурси

Відео: Визначаємо площу прямокутника за участю цілих чисел

Практика: Невідомі розміри квадратів і прямокутників

Реальний світ: Двір відходів