Skip to main content
LibreTexts - Ukrayinska

3.8: Кути і перпендикулярні лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    54546

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Лінії, які перетинаються під 90 градусів або прямим кутом.

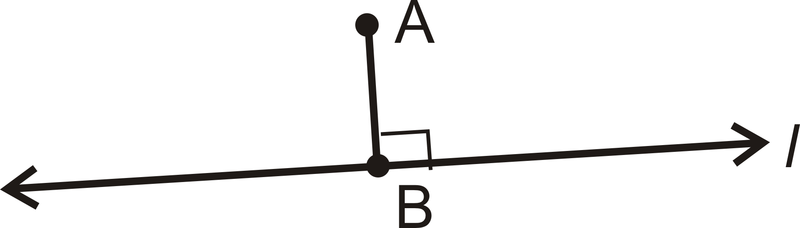
    Дві лінії перпендикулярні, коли вони перетинаються,\(90^{\circ}\) утворюючи кут. Нижче,\(l\perp \overline{AB}\).

    F-D_8125409784124 Баб-9С2С0Ф ЕБ926Ед 757Б6Е3А 07Д5А1Д6342+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    У визначенні перпендикуляра використовується слово «лінія». Однак відрізки ліній, промені і площини також можуть бути перпендикулярними. На зображенні нижче показані дві паралельні площини з третьою синьою площиною, яка перпендикулярна обом з них.

    Ф-Д_5854С70С8С90Ф356282Е7А92Д61625096Е87Ф939АЕ22Ф3638Б65479+зображення_крихіткий+зображення_крихіткий_PNG
    Малюнок\(\PageIndex{2}\)

    Основні факти про перпендикулярних лініях

    Теорема #1: Якщо\(l\parallel m\) і\(n\perp l\), то\(n\perp m\).

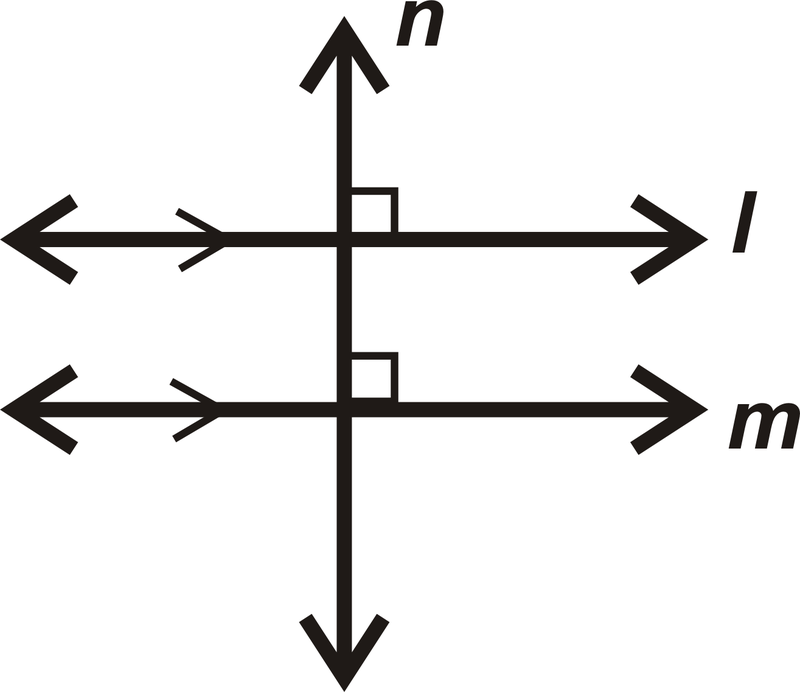
    Ф-д_д2С6АА2ААА2 АЦ725Д0Е31Ф44 ЕБ383ДА6Б059Ф9Ф9С2673048Ф4ФФ002ФЕ66Е7С+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Теорема #2: Якщо\(l\perp n\) і\(n\perp m\), то\(l\parallel m\).

    Ф-д_д2С6АА2ААА2 АЦ725Д0Е31Ф44 ЕБ383ДА6Б059Ф9Ф9С2673048Ф4ФФ002ФЕ66Е7С+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Постулат: Для будь-якої лінії і точки, яка не знаходиться на лінії, є одна лінія, перпендикулярна цій лінії, що проходить через точку. Є нескінченно багато ліній, які проходять через\(A\), але тільки одна, яка перпендикулярна\(l\).

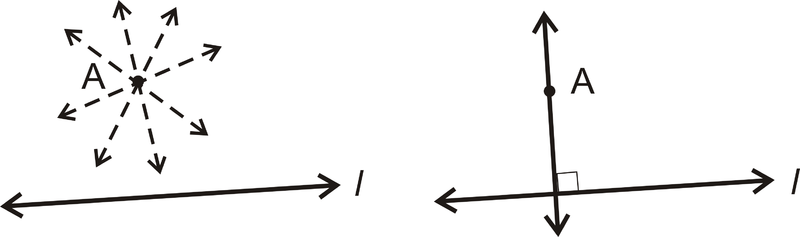
    F-д_Е4А15Е358672 AE2A892 ЕЕ6Е8122Б6027С16964 ДБ04ФАФ 18AF887512+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Що робити, якщо вам дали пару ліній, які перетинаються один з одним\(90^{\circ}\) під кутом? Яку термінологію ви б використали для опису таких рядків?

    Приклад\(\PageIndex{1}\)

    Визначте міру\(\angle 1\).

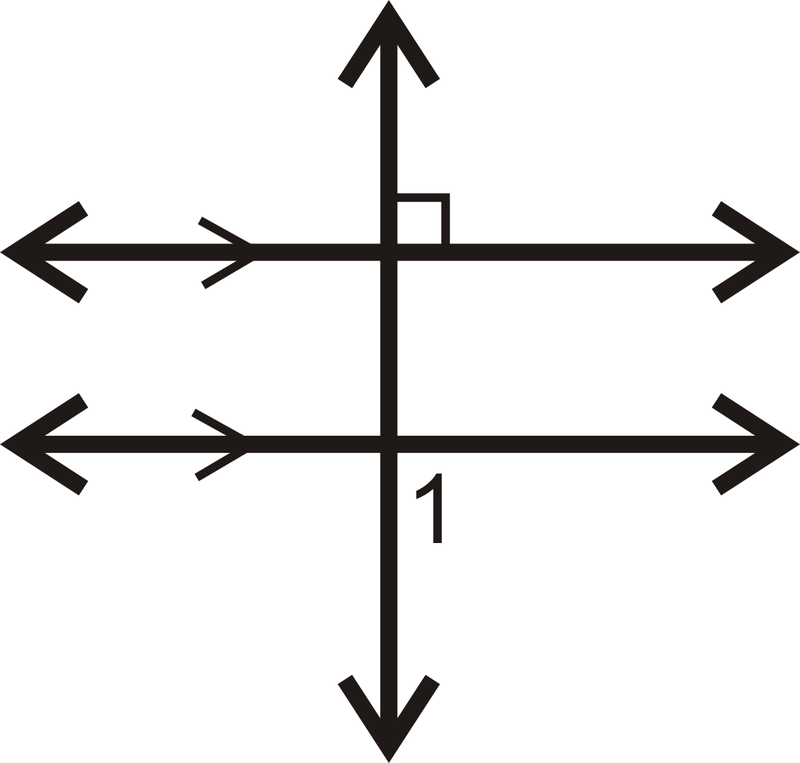
    F-D_32AC 4Д177С20БФБ1 БББА 068795 ДДЕ ДЕ 896762 ФБ82Д8471Б8ЕФ957336E8F+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Ми знаємо, що обидві паралельні лінії перпендикулярні поперечної.

    \(m\angle 1=90^{\circ}\).

    Приклад\(\PageIndex{2}\)

    Знайти\(m\angle 1\).

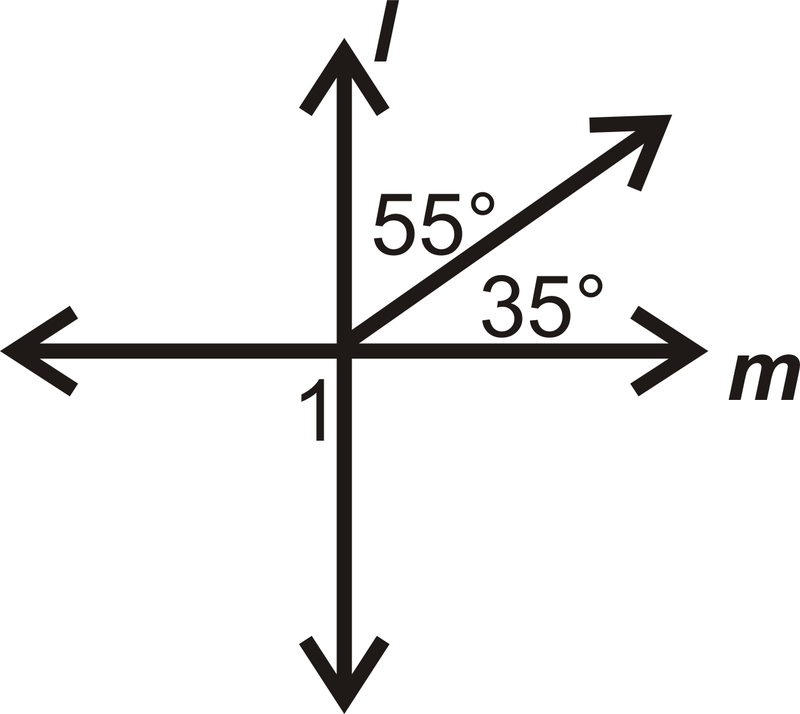
    F-D_BD4 Плата за 1F3CDC2E90D654 БД3БДС943Ф84602023D479EE8E02278D3C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рішення

    Два сусідніх кута складають до\(90^{\circ}\), так\(l\perp m\).

    \(m\angle 1=90^{\circ}\)

    тому що це вертикальний кут до пари сусідніх кутів, а вертикальні кути є конгруентними.

    Приклад\(\PageIndex{3}\)

    Який із наведених нижче є найкращим прикладом перпендикулярних ліній: широта на глобусі, протилежні сторони фоторамки, стовпи огорожі або суміжні сторони фоторамки?

    Рішення

    Кращим прикладом можуть бути сусідні сторони фоторамки. Пам'ятайте, що суміжні означає поруч і спільне використання вершини. Сусідні сторони фоторамки зустрічаються\(90^{\circ}\) під кутом і тому ці сторони перпендикулярні.

    Приклад\(\PageIndex{4}\)

    Є\(\overleftrightarrow{SO} \perp \overrightarrow{GD}\)?

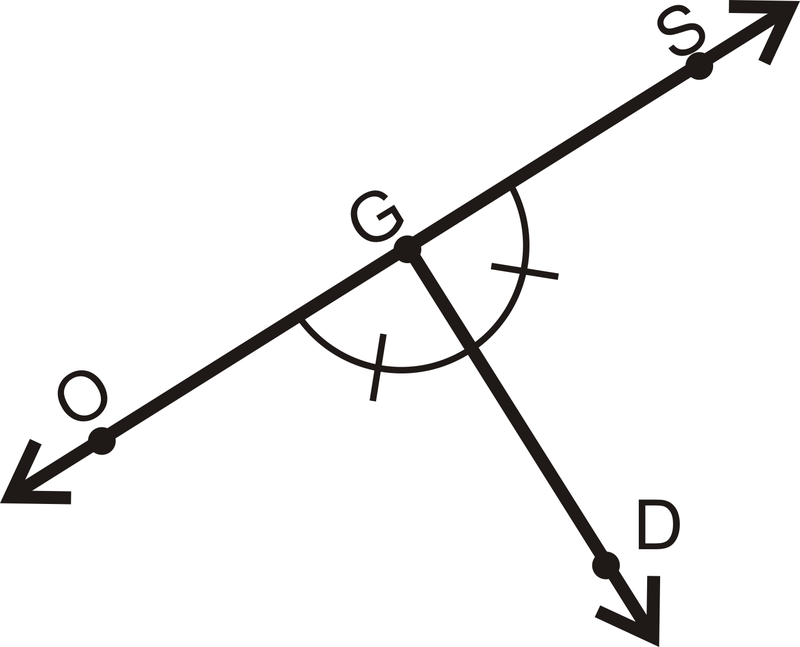
    Ф-Д_ФД71597669АЕ 3А94ДФФ 5ДФ05Ф09Е51С17232305КД2А7БД907957A+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{8}\)

    Рішення

    \(\angle OGD\cong \angle SGD\)а кути утворюють лінійну пару. Це означає, що обидва кути є\(90^{\circ}\), тому лінії перпендикулярні.

    Приклад\(\PageIndex{5}\)

    Напишіть 2-стовпцевий доказ, щоб довести теорему #1. Примітка: Вам потрібно зрозуміти відповідні кути, щоб зрозуміти цей доказ. Якщо ви ще не вивчили відповідні кути, обов'язково спочатку ознайомтеся з цією концепцією або пропустіть цей приклад.

    З огляду на:\(l\parallel m\),\(l\perp n\)

    Доведіть:\(n\perp m\)

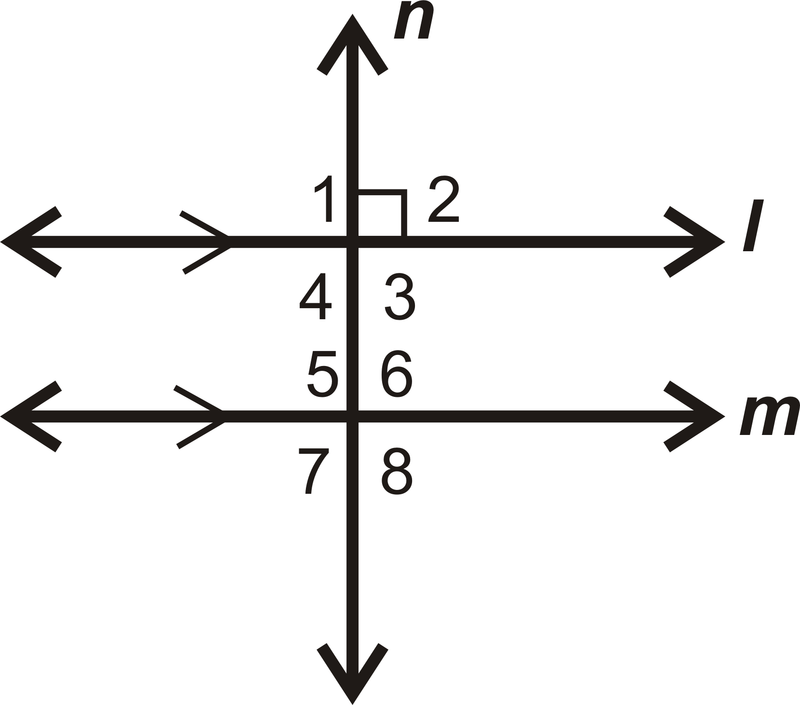
    F-д_430720902 ЕЕД 3308265БК4 ФБ 427740745Е0С596Д76А38А6FC468E+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

    Заява Причина
    1. \(l\parallel m\),\(l\perp n\) 1. Враховується
    2. \(\angle 1\),\(\angle 2\),\(\angle 3\), і\(\angle 4 are right angles\) 2. Визначення перпендикулярних ліній
    3. \(m\angle 1=90^{\circ}\) 3. Визначення прямого кута
    4. \(m\angle 1=m\angle 5\) 4. Відповідні кути постулат
    5. \(m\angle 5=90^{\circ}\) 5. Перехідний\(PoE\)
    6. \(m\angle 6=m\angle 7=90^{\circ}\) 6. Конгруентні лінійні пари
    7. \(m\angle 8=\(90^{\circ}\) 7. Теорема про вертикальні кути
    8. \(\angle 5\),\(\angle 6\),\(\angle 7\), і\(\angle 8\) є прямими кутами 8. Визначення прямого кута
    9. \(n\perp m\) 9. Визначення перпендикулярних ліній

    Рецензія

    Використовуйте малюнок нижче, щоб відповісти на питання 1-2. Два п'ятикутника паралельні і всі прямокутні сторони перпендикулярні обом.

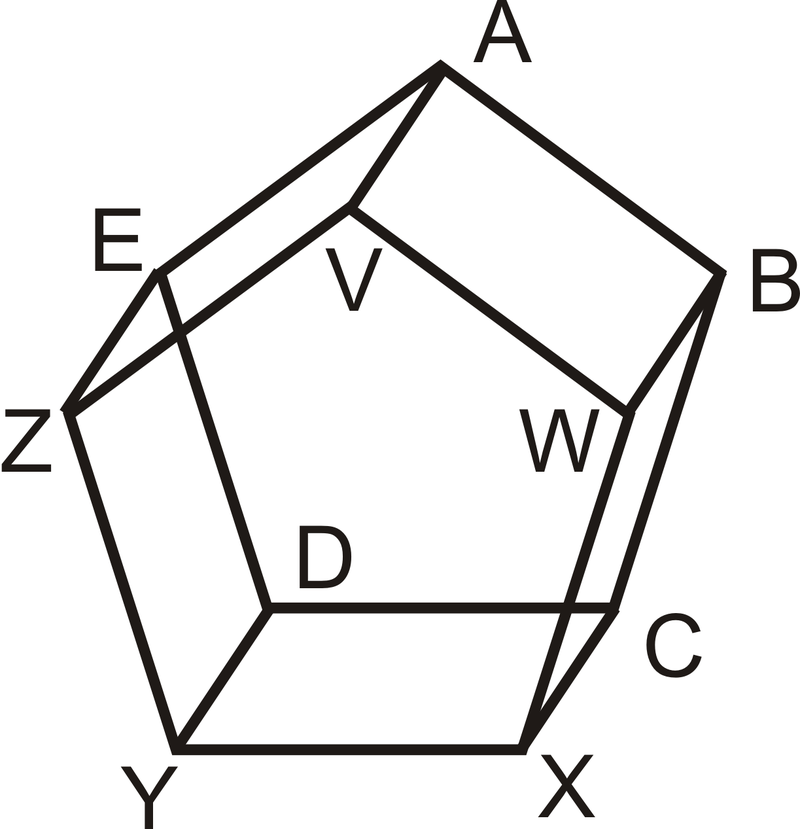
    Ф-Д_ДК 6 ліжко 64085Ф2А2Д510741341С01148Ф593А03С99081005265Ф67ЦЕ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)
    1. Перерахуйте пару перпендикулярних ліній.
    2. Бо\(\overline{AB}\), скільки перпендикулярних ліній буде проходити через точку\(V\)? Назвіть this/ці рядки (и).

    Використовуйте малюнок нижче для питання 3.

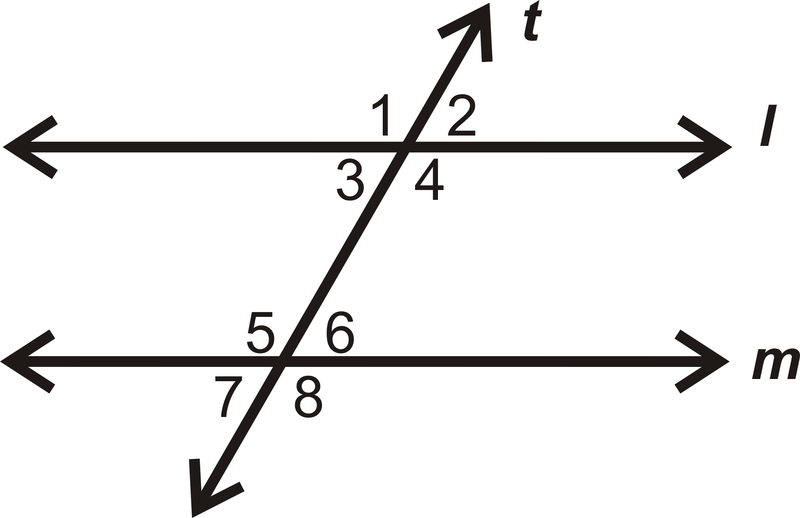
    F-D_F8Е0Д0С765E41 БД04КА58А5Е73 КД09555А02А929Д06Ф952CF3E5DD7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{11}\)
    1. Якщо\(t\perp l\), є\(t\perp m\)? Чому чи чому ні?

    Знайдіть міру\(\angle 1\) для кожної проблеми нижче.

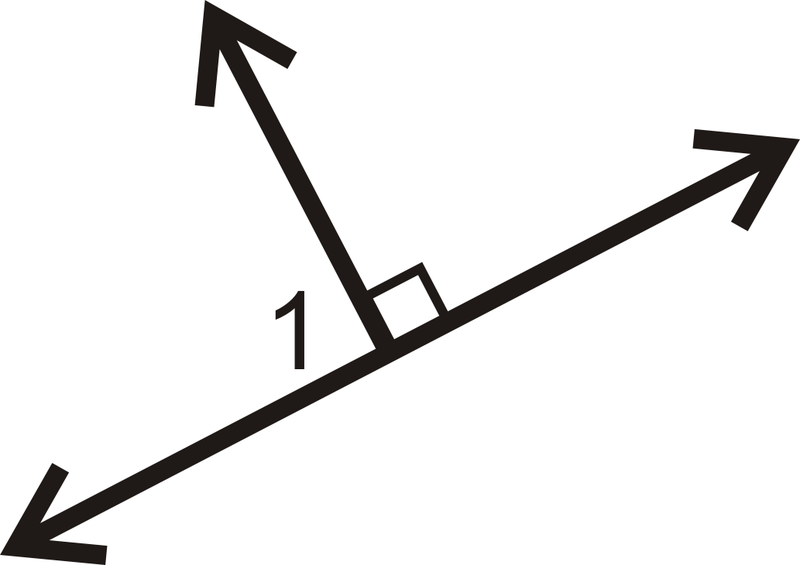
    1. F-D_E2B4D7AEEE8259583937 CFD 40Б01Б66Ф8Д0А4 АББ5165599C4D+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
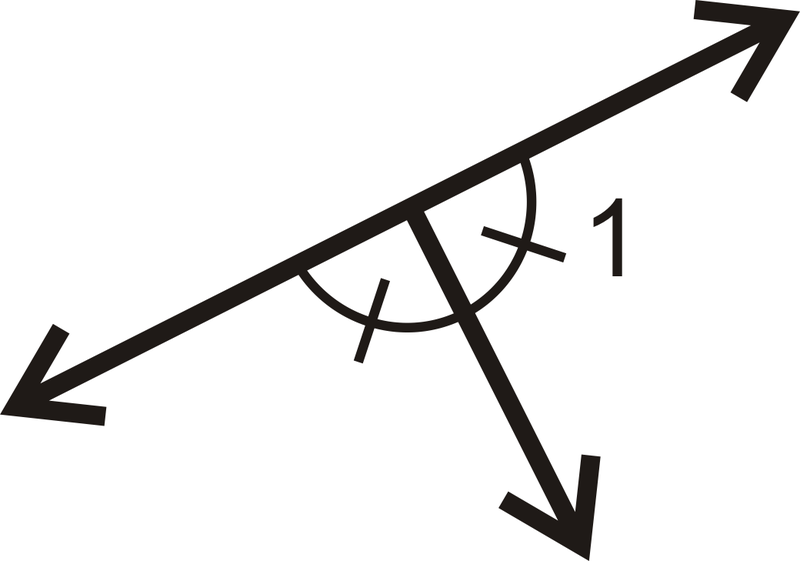
    2. F-D_CF3780Е7Д5А6 ФЧ 60Д483 ФЕ 8Ф2А0Е1 Е98923КС85БА 6КАС 558 ЕФА 0575F+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
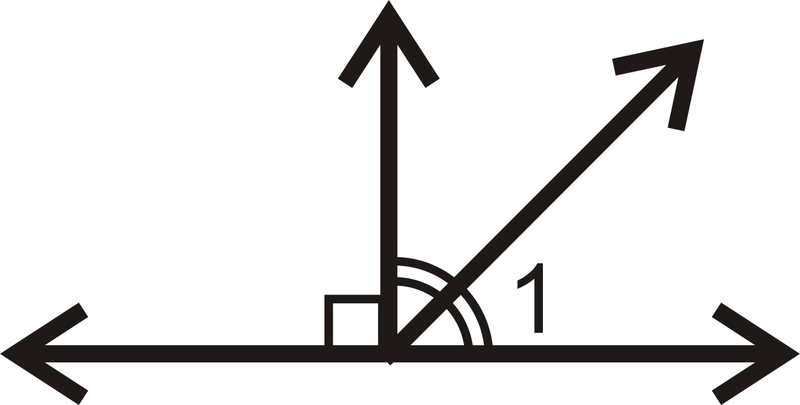
    3. Ф-д_А206А 48511Е9А2Ф5Ф18471Д942Б32984316 Баб26727Б39970Ф7579A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
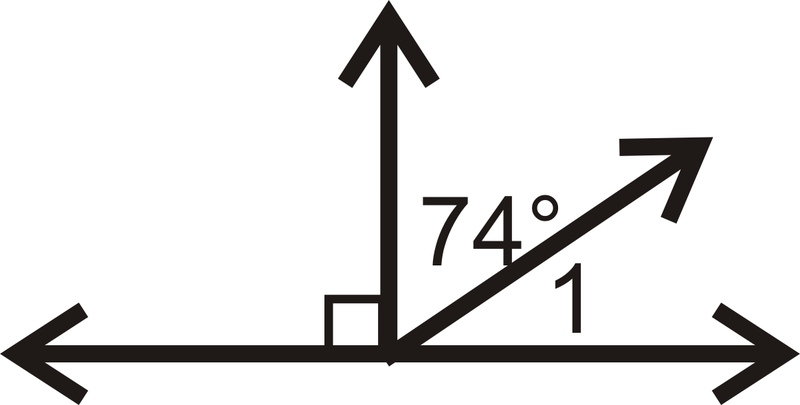
    4. F-д_Ф593С6932Ф3А8С8Б05КС2ЕД 0Б83Д34С50191Ф8К46CF696417A370008+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
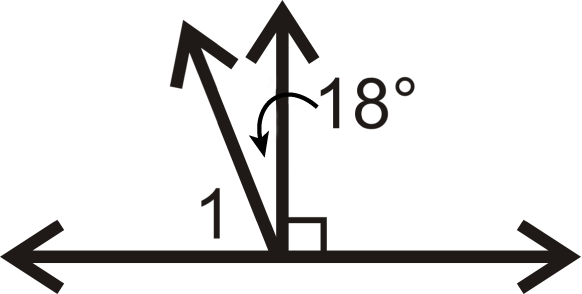
    5. F-D_9704D9FF8Б541561 Д53Д58409С93Б7Ф500А5Б5179 ЕДЕ0952D60D3F21+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
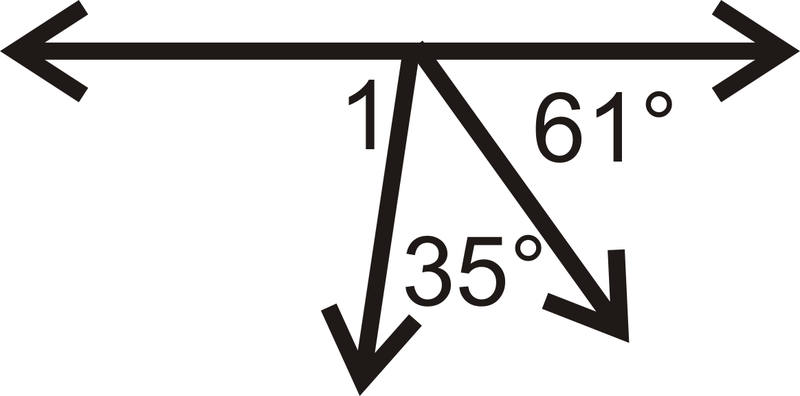
    6. F-D_E17656A37024CE212CC9A5300831А65С3Ф9Ф7ЕАCF4B6195FC5DC23AE+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
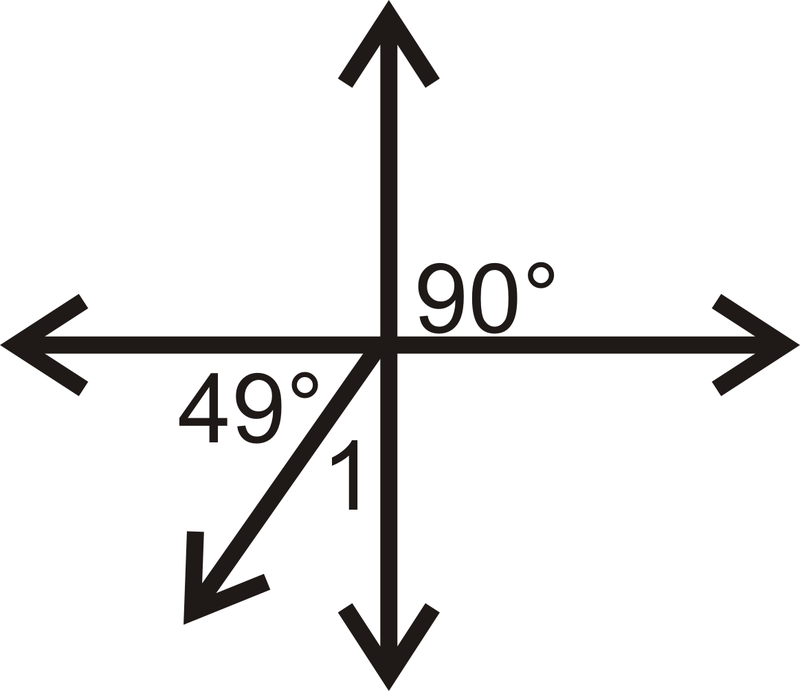
    7. Ф-д_33Ф0СА09АФ 4Б4954С1Е63 ФК 196С33139 ФК697Б3С73Ф2983404Е6345+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
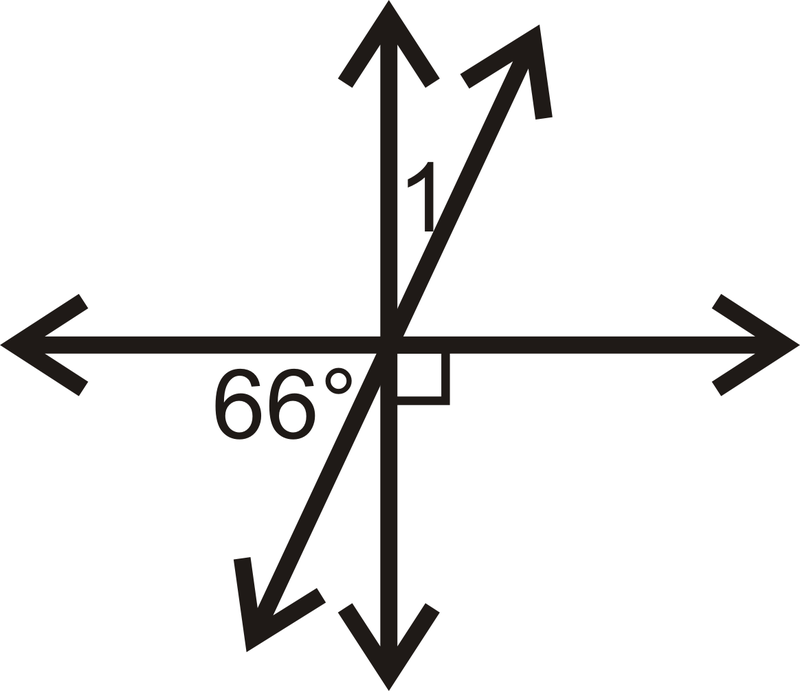
    8. F-D_4 АЦ78Б462882132CE7A2D3DF69ed7405Fa7DCF64294D1C14F3C922+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
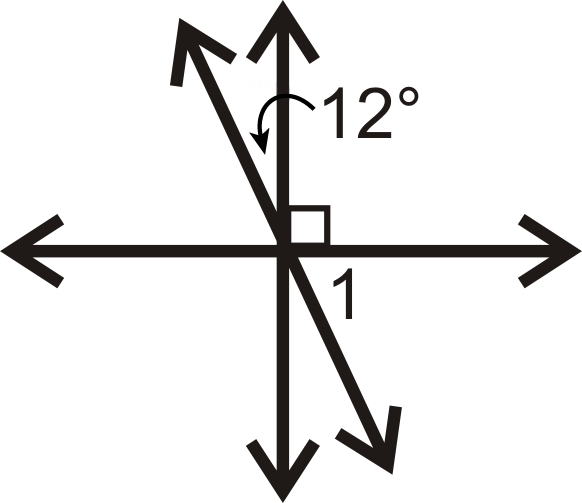
    9. F-D_61667C8782 Фе Плата за 0БА 189 ЕД 83С3217АЕ 91ДК5104АФ 9952ЕЕЦБФА2А34+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)

    У питаннях 13-16 визначте, якщо\(l\perp m.\)

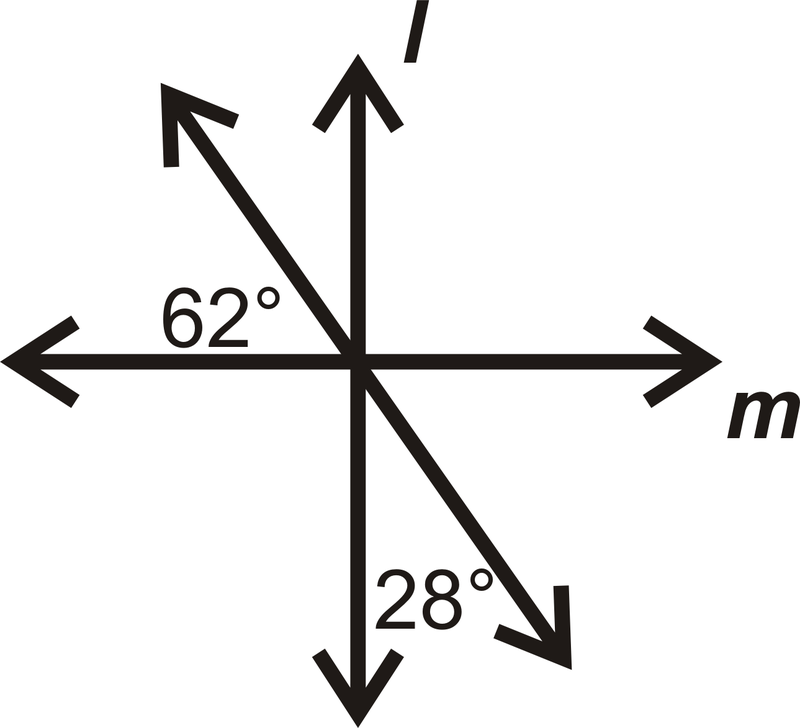
    1. F-D_E448E05B43ФД132E5248949E06CF8A2E56 ЕБК 3DCC5D7AB7FE9D+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)
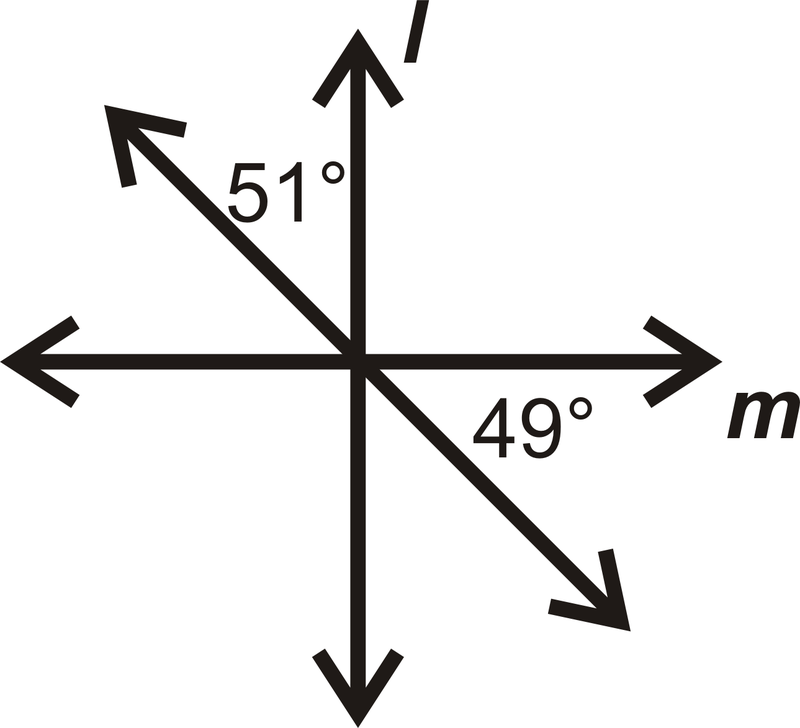
    2. Ф-Д_0287Ф76Б2Б6605А4ЕД 8037А004Ф923С7Е2ДДФ59ДБ 98Ф797А2БД А5С+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{22}\)
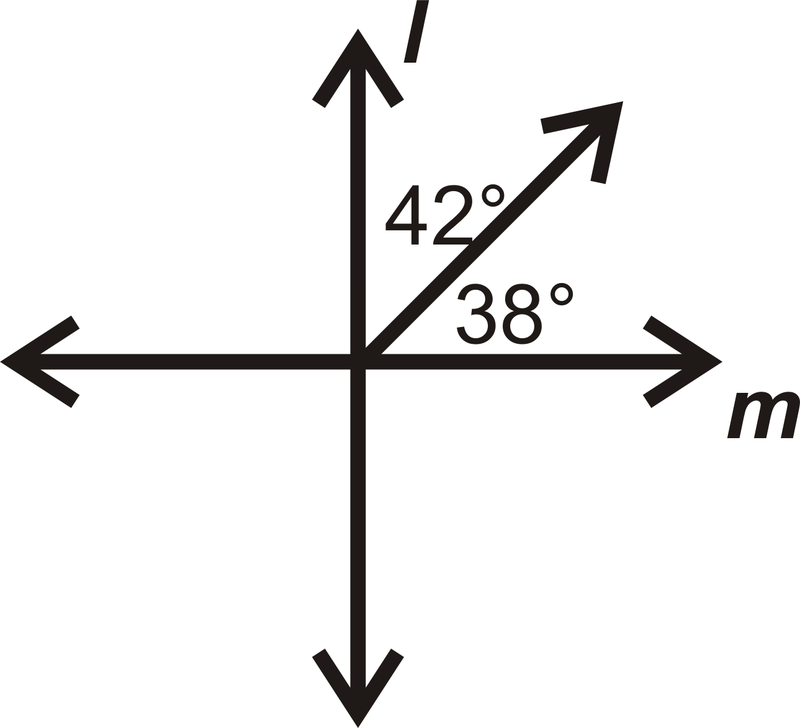
    3. Ф-д_ББ 122Ф9Б2БК2ФБК 3С2Е6Ф85АФБ5Б5Б5Б500047Ф2851Ф202ЕФ6Б889FF4160+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{23}\)
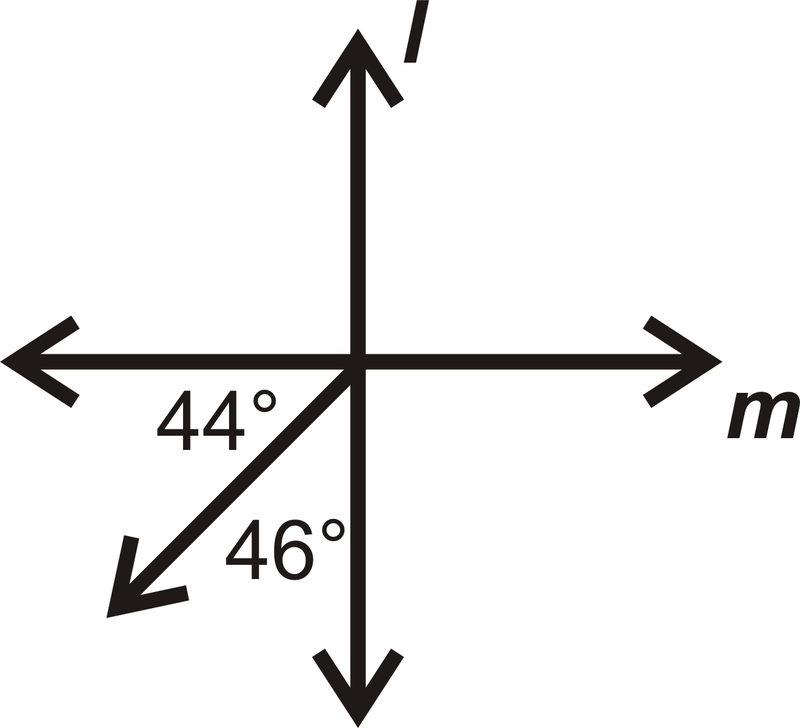
    4. F-д_30Ф4 ФАА 9Е18Е7С71Д6Д82ДФ 58Д120АЕ 045БФ Ф 13542Б176БФ 5БК+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{24}\)

    Заповніть пропуски в доказі нижче.

    1. З огляду на:\(l\perp m\),\(l\perp n\) Доведіть:\(m\parallel n\)
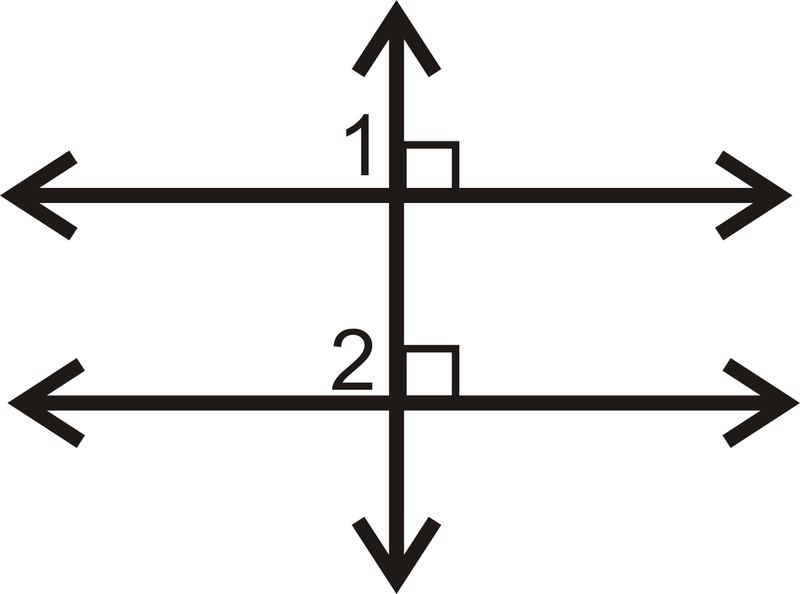
    Ф-Д_45ДФ ФКФ 12527315Ф6АЕ 801143ДФ БК 7874Е08Д52822Е3202C31C93F3B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{25}\)
    Заява Причина
    1. 1.
    2. \(\angle 1\)і\(\angle 2\) є прямими кутами 2.
    3. 3. Визначення прямих кутів
    4. 4. Перехідний\(PoE\)
    5. \(m\parallel n\) 5.

    Ресурси

    Лексика

    Термін Визначення
    перпендикуляр Дві лінії перпендикулярні, коли вони перетинаються,\(90^{\circ}\) утворюючи кут.
    Кут Геометрична фігура, утворена двома променями, які з'єднуються в одній точці або вершині.
    перпендикулярні лінії Перпендикулярні лінії - це лінії, які перетинаються під\(90^{\circ}\) кутом.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи перпендикулярних ліній - основні

    Види діяльності: Перпендикулярні лінії обговорення

    Навчальні посібники: Керівництво по вивченню ліній та кутів

    Практика: Кути і перпендикулярні лінії

    Реальний світ: поворот столів