3.7: Однакові бічні внутрішні кути

Last updated
Save as PDF

Page ID: 54547

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Кути на тій же стороні поперечного і всередині ліній, які вона перетинає.

Однакові бічні внутрішні кути - це два кути, які знаходяться на одній стороні поперечного та на внутрішній стороні (між) двома лініями.

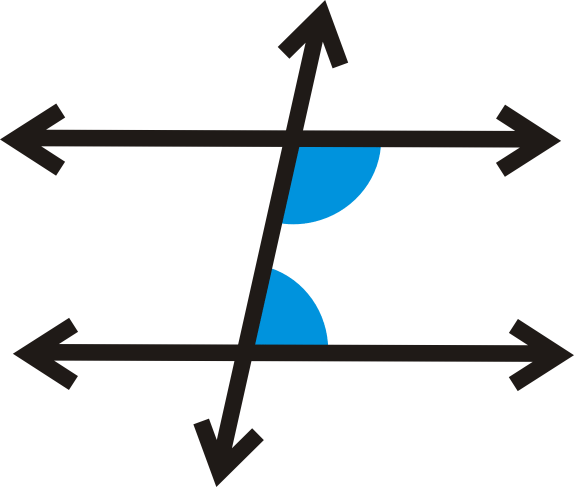
Ф-д_А8Д9Б91ДФ 19Ф74Ф34ФФ 164377ФД63А7 ДБК7С055ФЦ5ФЦ5ФС5FF57ECBE9634BF+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Теорема однакових бокових внутрішніх кутів: Якщо дві паралельні лінії розрізаються поперечним, то ті ж бічні внутрішні кути є додатковими.

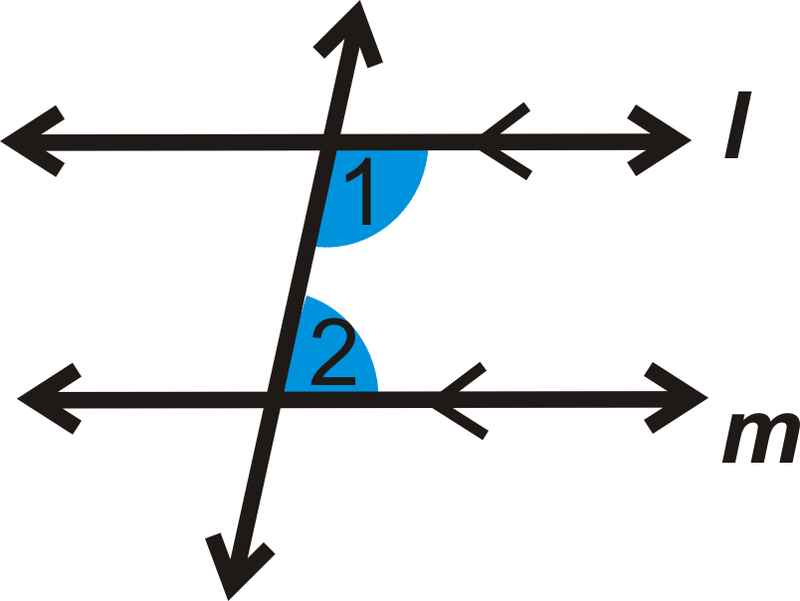
F-D_91CE9 ЕА А5С4А427538Д80Д88915519Д0А21CFбабаб 9534Ф1Ф08КБ0850+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Якщо\(l \parallel m\), то\(m\angle 1+m\angle 2=180^{\circ}\).

Конверс теореми однакових бічних внутрішніх кутів: Якщо дві лінії розрізаються поперечним, а однакові бічні внутрішні кути є додатковими, то лінії паралельні.

Якщо

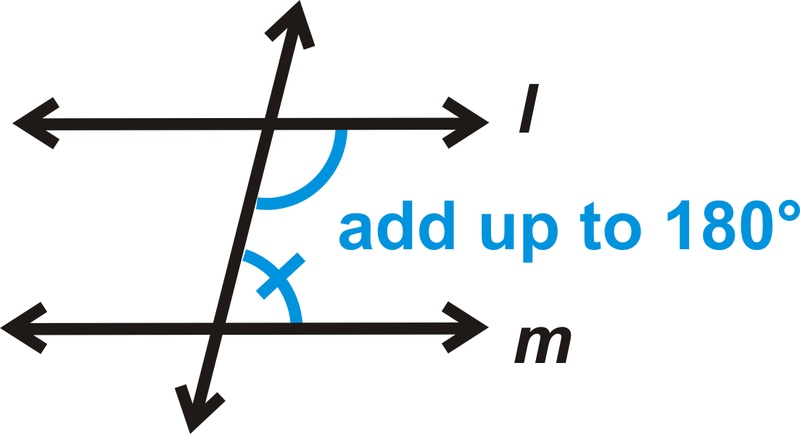
F-D_67D340685341A2F8C3028D57936483c844C7C3451729fd0fd1CFC6b0+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

потім\(l \parallel m\)

Припустимо, вам були представлені два кути, які знаходяться на одній стороні поперечного і між двома паралельними лініями, перетинаються поперечним. Як би ви описали ці кути і що ви могли б зробити висновок про їх заходи?

Приклад\(\PageIndex{1}\)

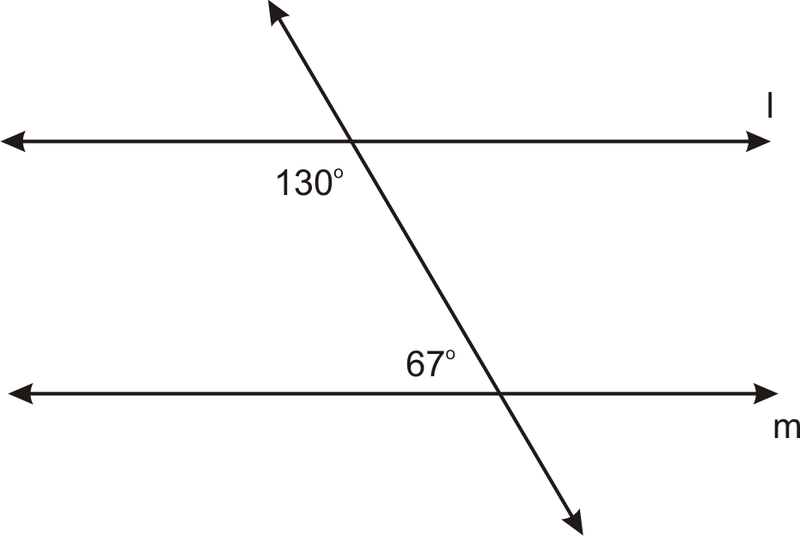
Є\(l \parallel m\)? Звідки ти знаєш?

Рішення

Ці кути є однаковими бічними внутрішніми кутами. Отже, якщо вони складають до\(180^{\circ}\), то\(l\parallel m\).

\(130^{\circ}+67^{\circ}=197^{\circ}\), Тому лінії не паралельні.

F-д_74Е7Е9А69 Фе 84С8КС252Ф406Ф9133Ф3718d58847748E2A3A3B59E5A1+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Приклад\(\PageIndex{2}\)

Наведіть два приклади однакових бічних внутрішніх кутів на схемі:

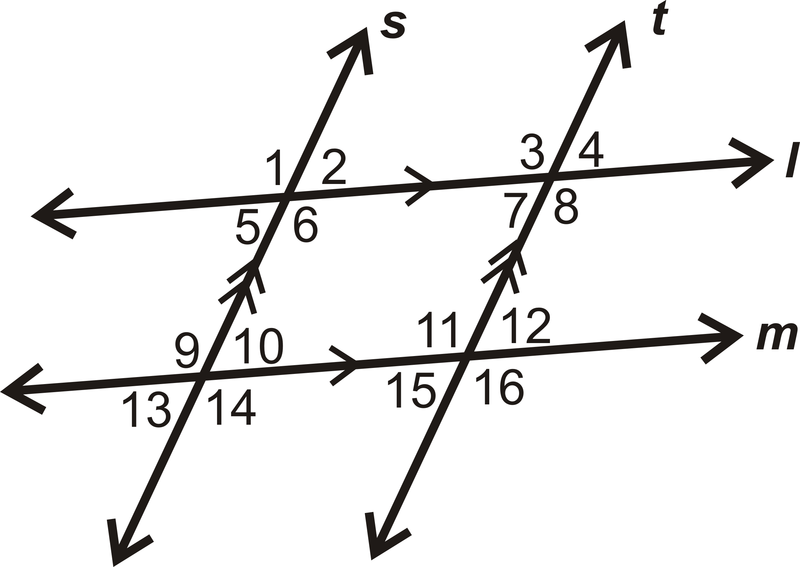
F-D_ACF 685Ф70 АЦ87Б4075812Б7 ЕЦС 116ДБ Б ААК 3970Ф8ЕД 695303C88B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

Є БАГАТО прикладів однакових бічних внутрішніх кутів на схемі. Два - це\(\angle 6\) і\(\angle 10\), і\(\angle 8\) і\(\angle 12\).

Приклад\(\PageIndex{3}\)

Знайдіть значення\(x\).

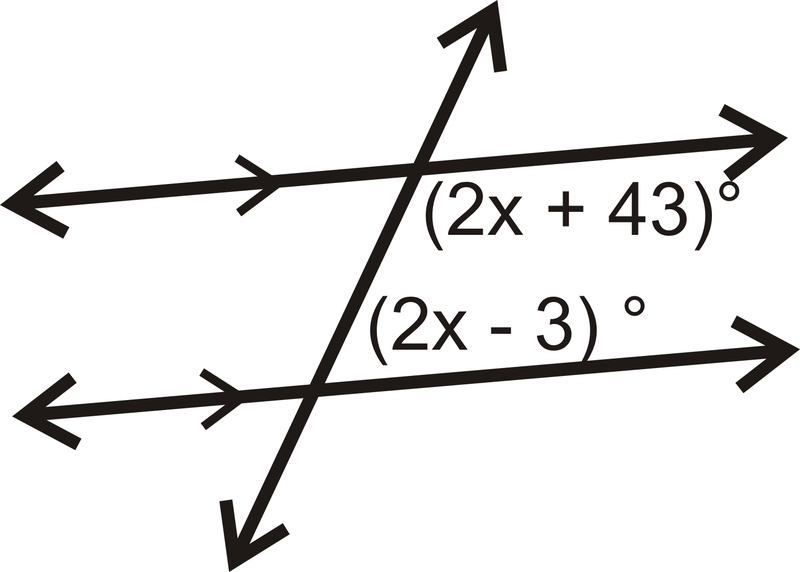
F-D_44014A86CF753C8 BEA8A 839356AE4C8B578DF175E0F1E2AAB4CDF96CCC+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Задані кути - це ті ж бічні внутрішні кути. Оскільки лінії паралельні, кути складають до\(180^{\circ}\).

\(\begin{align*}(2x+43)^{\circ}+(2x−3)^{\circ} &=180^{\circ} \\ (4x+40)^{\circ} &=180^{\circ} \\ 4x &=140 \\ x &=35\end{align*}\)

Приклад\(\PageIndex{4}\)

Знайдіть значення\(y\).

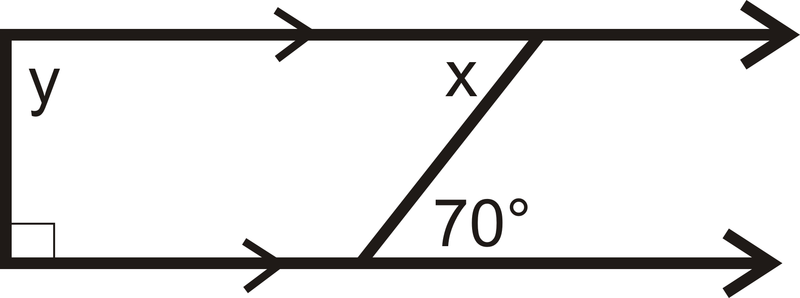F-д_ЕФ9С9Е5Е1682147552С76009265Б7А902Б7А14102006 КБ31Б7352+зображення_крихіткий+зображення_крихіткий.PNG

Рішення

\(y\)це той же бічний внутрішній кут із зазначеним прямим кутом. Це означає, що\(90^{\circ}+y=180\) так\(y=90\).

Приклад\(\PageIndex{5}\)

Знайти значення\(x\) if\(m\angle 3=(3x+12)^{\circ}\) і\(m\angle 5=(5x+8)^{\circ}\).

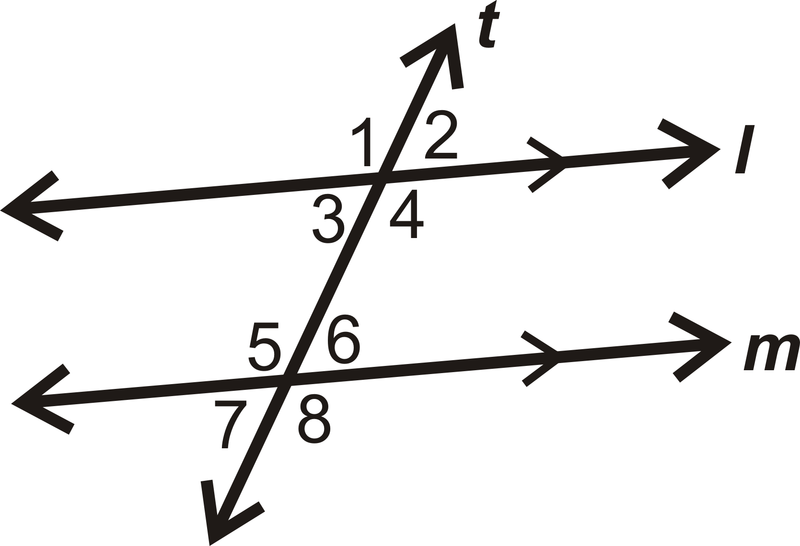
F-д_7д690А17С6Б2Е3БК 2ЕС2070038 ЕД 705ЕБ9А6272064C8C84195102+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Рішення

Це ті ж бічні внутрішні кути, тому встановіть рівняння і вирішуйте для\(x\). Пам'ятайте, що однакові бічні внутрішні кути складають до\(180^{\circ}\).

\(\begin{align*} (3x+12)^{\circ}+(5x+8)^{\circ} &=180^{\circ} \\(8x+20)^{\circ} &=180^{\circ} \\8x &=160 \\ x &=20 \end{align*}\)

Рецензія

Для питань 1-2 використовуйте діаграму, щоб визначити, чи кожна кутова пара є конгруентною, додатковою чи ні.

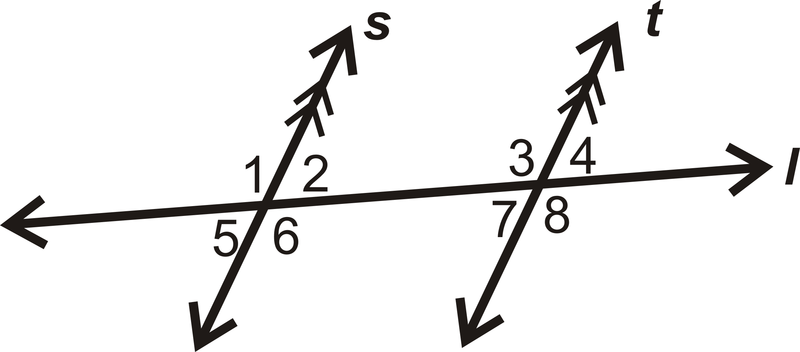
F-D_C433 BBB 430C5A21 ЕФ 1034 Баабд 9 А175Е53Ф1Б202Б64С172D5+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

\(\angle 5\)і\(\angle 8\)
\(\angle 2\)і\(\angle 3\)
Чи паралельні лінії? Обґрунтуйте свою відповідь.

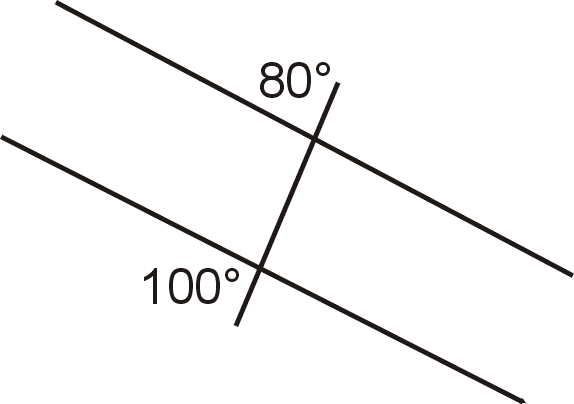
Малюнок\(\PageIndex{10}\)

У 4-5 використовуйте задану інформацію, щоб визначити, які лінії паралельні. Якщо таких немає, напишіть none. Розглянемо кожне питання індивідуально.

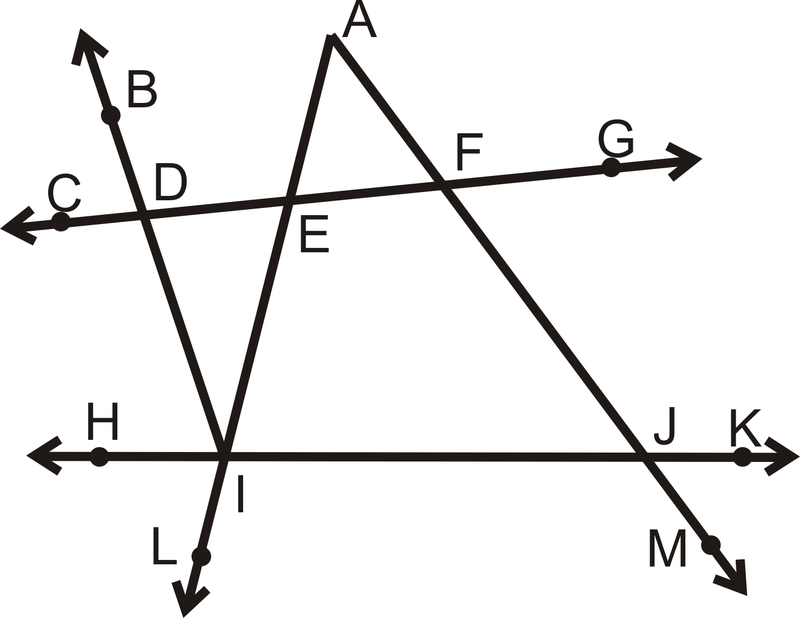
F-д_А9669Д1041Ф370E9E54907Е 878108А838Д6CF9377D8D1F8AAC5A10+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{11}\)

\(\angle AFD\)і\(\angle BDF\) є додатковими
\(\angle DIJ\)і\(\angle FJI\) є додатковими

Для 6-8, яке значення\(x\) має бути, щоб лінії були паралельними?

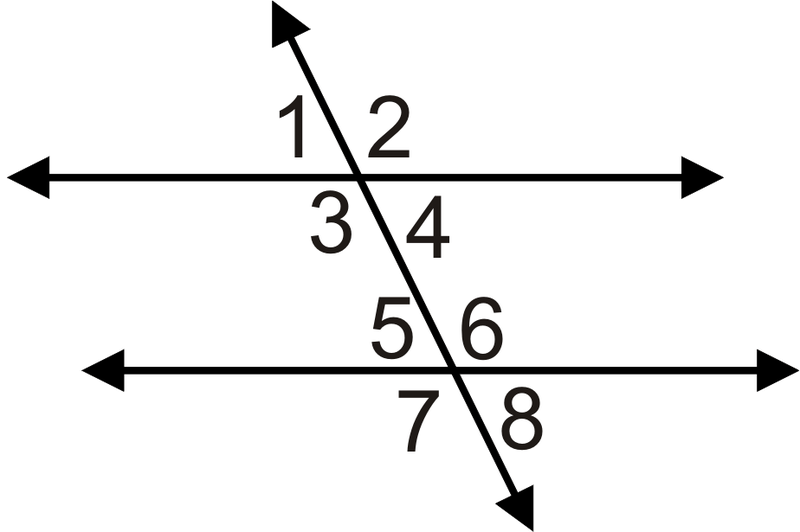
F-д_963 дБД ФЧ7Б826Д8117ФФ8Ф1Ф6БФ93Е5С8Д514ФД8352Б7Б67+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

\(m\angle 3=(3x+25)^{\circ}\)і\(m\angle 5=(4x−55)^{\circ}\)
\(m\angle 4=(2x+15)^{\circ}\)і\(m\angle 6=(3x−5)^{\circ}\)
\(m\angle 3=(x+17)^{\circ}\)і\(m\angle 5=(3x−5)^{\circ}\)

Для 9-10 визначте, чи є твердження істинним або хибним.

Такі ж бічні внутрішні кути знаходяться на одній стороні поперечного.
Однакові бічні внутрішні кути конгруентні, коли лінії паралельні.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 3.6.

Лексика

Термін	Визначення
однакові бічні внутрішні кути	Однакові бічні внутрішні кути - це два кути, які знаходяться на одній стороні поперечної і на внутрішній стороні двох ліній.
додаткові кути	Два кути, які складають до\(180^{\circ}\).
поперечний	Лінія, яка перетинає дві інші лінії.

Додатковий ресурс

Інтерактивний елемент

Відео: Принципи однакових бічних кутів інтер'єру - основні

Діяльність: Той же бічний інтер'єр Кути обговорення Питання

Навчальні посібники: Кути та поперечні навчальні посібники

Практика: однакові бічні внутрішні кути

Реальний світ: альтернативні зовнішні кути