3.9: Паралельні лінії в координатній площині

Last updated
Save as PDF

Page ID: 54580

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Лінії з однаковим нахилом, які ніколи не перетинаються.

Паралельні лінії - це дві лінії, які ніколи не перетинаються. У координатній площині, що б виглядало так:

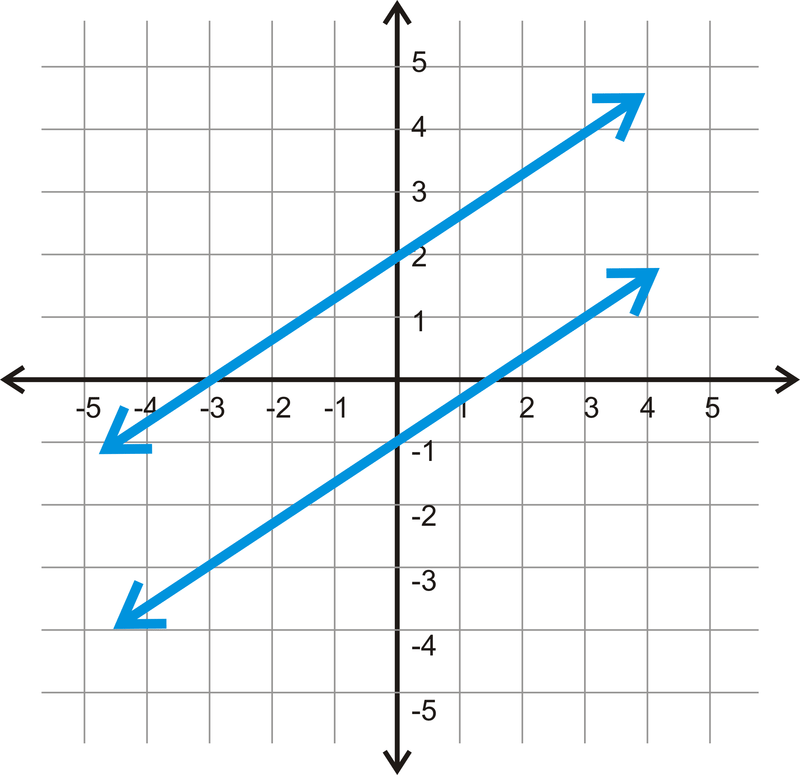
F-D_3CEEB 0БА 9414CC883C09344Ф3559186 АЕ 97БД2434Е1Д67КДФЕ4483D5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Якщо уважніше розглянути ці дві лінії, то схили обидва\(\dfrac{2}{3}\).

Це можна узагальнити на будь-яку пару паралельних ліній. Паралельні лінії завжди мають однаковий нахил і різні\(y\) −перехоплення.

Що робити, якщо вам дали дві паралельні лінії в координатній площині? Що ви могли б сказати про їх схилах?

Відео

Приклад\(\PageIndex{1}\)

Знайдіть рівняння прямої, яка паралельна\(y=\dfrac{1}{4}x+3\) і проходить через неї\((8, -7)\).

Рішення

Ми знаємо, що паралельні лінії мають однаковий нахил, тому лінія буде мати нахил\(dfrac{1}{4}\). Тепер нам потрібно знайти\(y\) −intercept. Увімкніть 8 для x та -7\(y\) для розв'язання нового\(y\) параметра −intercept (b).

\(\begin{align*}−7=\dfrac{1}{4} (8)+b \\ −7&=2+b \\ −9 &=b \end{align*}\)

Рівняння паралельної прямої є\(y=\dfrac{1}{4}x−9\).

Приклад\(\PageIndex{2}\)

Чи є лінії\(3x+4y=7\) і\(y=\dfrac{3}{4} x+1\) паралельні?

Рішення

Спочатку нам потрібно переписати перше рівняння у вигляді нахилу-перехоплення.

\(\begin{align*}3x+4y &=7 \\ 4y &=−3x+7 \\ y &=−\dfrac{3}{4}x+\dfrac{7}{4} \end{align*}\).

Нахил цієї лінії\(−\dfrac{3}{4}\) при цьому нахил іншої лінії\(\dfrac{3}{4}\). Оскільки схили різні, лінії не паралельні.

Приклад\(\PageIndex{3}\)

Знайдіть рівняння прямої, яка паралельна\(y=−\dfrac{1}{3} x+4\) і проходить через неї\((9, -5)\).

Рішення

Нагадаємо, що рівнянням прямої є y = mx+b, де m - нахил, а b -\(y\) перехоплення. Ми знаємо, що паралельні лінії мають однаковий нахил, тому лінія матиме нахил −13. Тепер нам потрібно знайти\(y\) −intercept. Увімкніть 9 для\(x\) та -5\(y\) для розв'язання нового\(y\) параметра −intercept (b).

\(\begin{align*}−5&=−\dfrac{1}{3} (9)+b \\ −5&=−3+b \\−2&=b\end{align*}\)

Рівняння паралельної прямої є\(y=−\dfrac{1}{3} x−2\).

Приклад\(\PageIndex{4}\)

Знайдіть рівняння ліній нижче і визначте, чи паралельні вони.

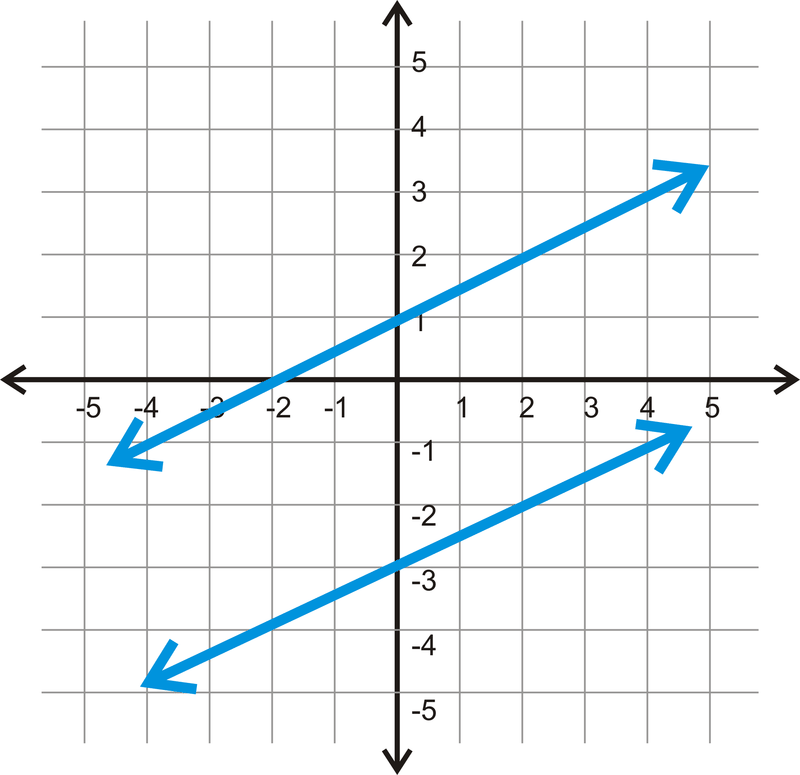
F-D_38 ДДФ 73576D1 ДБ57503Д88Е4Е7Д53 Е5А222ДАА 943706D3ed39C8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Верхній рядок містить\(y\) −перехоплення 1. Звідти використовуйте «підйом над бігом», щоб знайти схил. З\(y\) −intercept, якщо ви підніметеся вгору на 1 і більше 2, ви знову натиснете рядок,\(m=\dfrac{1}{2}\). Рівняння є\(y=\dfrac{1}{2} x+1\).

Для другого рядка\(y\) −intercept дорівнює -3. «Підйом» дорівнює 1, а «пробіг» - 2, що робить ухил\(\dfrac{1}{2}\). Рівняння цієї лінії є\(y=\dfrac{1}{2} x−3\).

Лінії паралельні, оскільки мають однаковий нахил.

Приклад\(\PageIndex{5}\)

Знайдіть рівняння прямої, яка паралельна прямій через точку, позначену синьою крапкою.

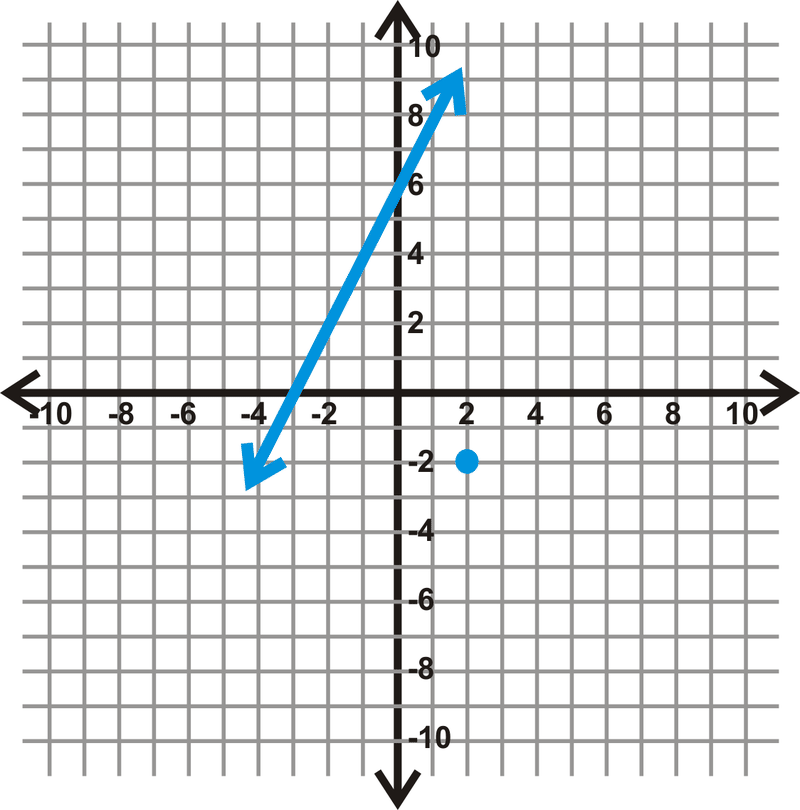
F-д_Ф0БД 89659Д33Е5Б8Ф1Е5Б8818076С5 DeF893454 ЕБ65БФ21Б79А0d1ad5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

По-перше, зверніть увагу, що рівняння\(y=2x+6\) прямої є і точка є\((2, -2)\). Паралель мала б однаковий ухил і проходила наскрізь\((2, -2)\).

\(\begin{align*}y &=2x+b \\ −2 &=2(2)+b \\ −2&=4+b \\−6&=b \end{align*}\)

Рівняння паралельної прямої є\(y=2x+−6\).

Рецензія

Визначте, чи кожна пара ліній паралельна. Потім намалюйте кожну пару на одному і тому ж наборі осей.

\(y=4x−2\)і\(y=4x+5\)
\(y=−x+5\)і\(y=x+1\)
\(5x+2y=−4\)і\(5x+2y=8\)
\(x+y=6\)і\(4x+4y=−16\)

Визначте рівняння прямої, яка паралельна даній прямій, через задану точку.

\(y=−5x+1; (−2,3)\)
\(y=\dfrac{2}{3}x−2; (9,1)\)
\(x−4y=12; (−16,−2)\)
\(3x+2y=10; (8,−11)\)

Знайдіть рівняння двох рядків на кожному графіку нижче. Потім визначте, чи дві лінії паралельні.

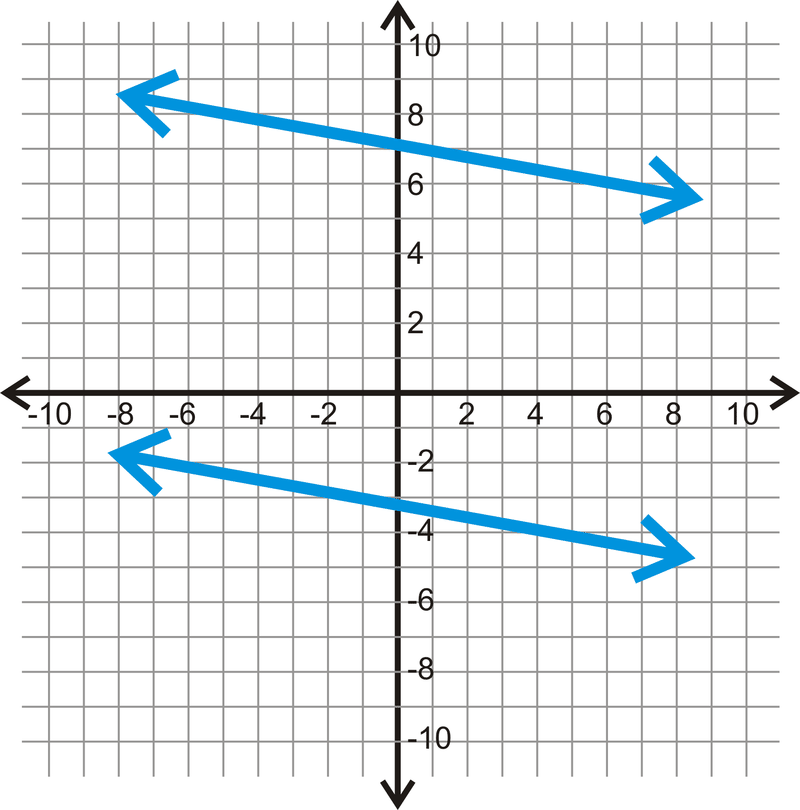
Малюнок\(\PageIndex{4}\)

Для лінії і точки нижче знайдіть паралельну лінію, через задану точку.

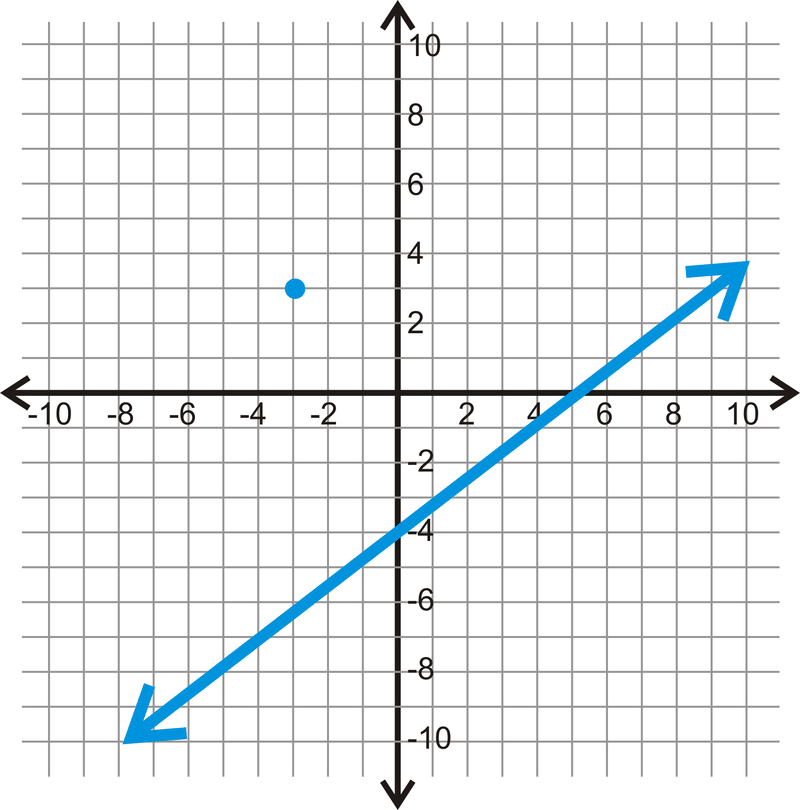
Малюнок\(\PageIndex{5}\)
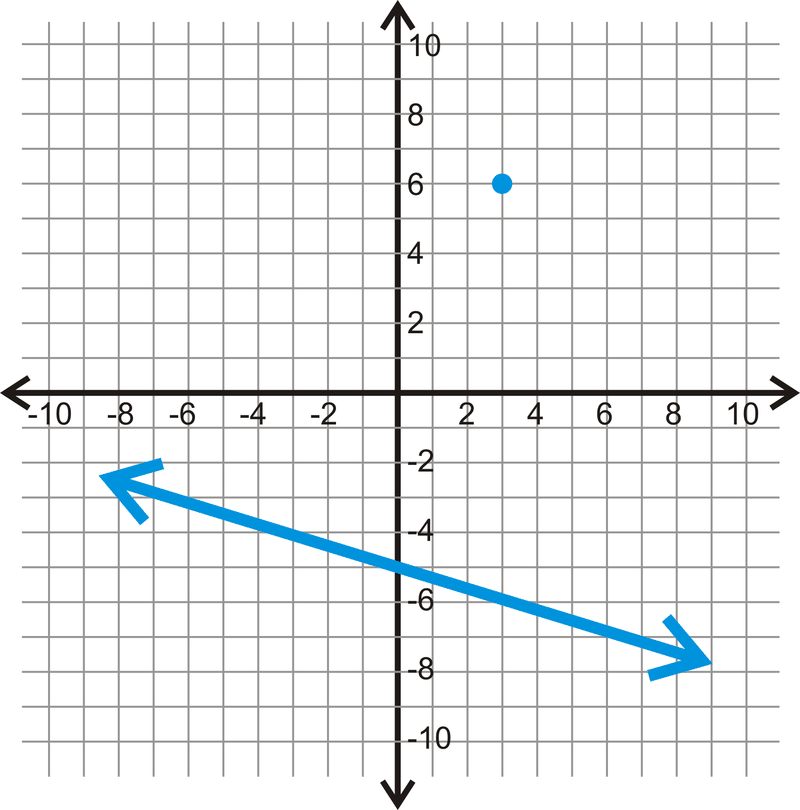
Малюнок\(\PageIndex{6}\)
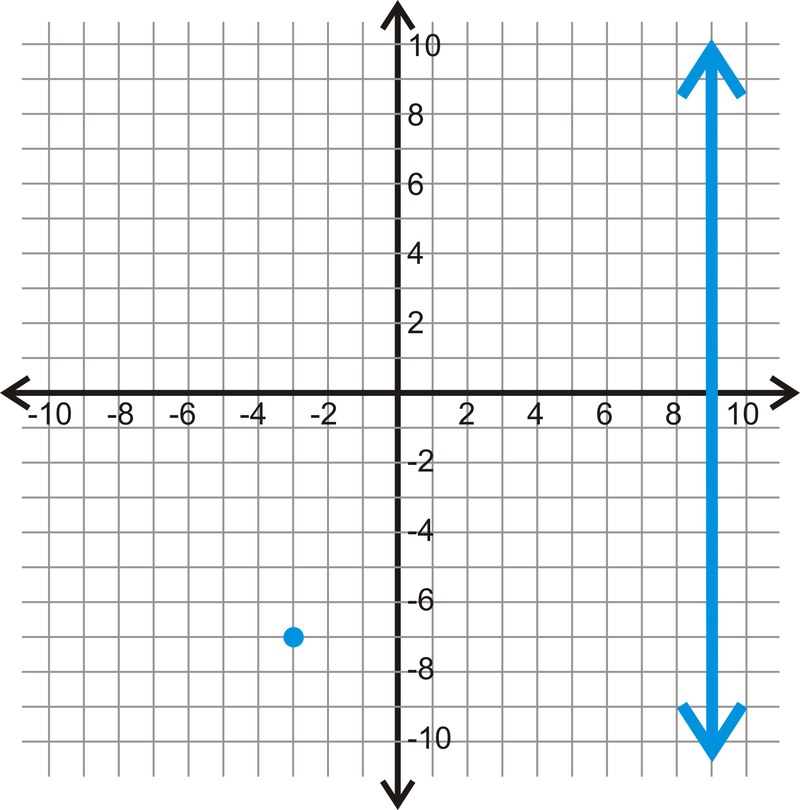
Малюнок\(\PageIndex{7}\)
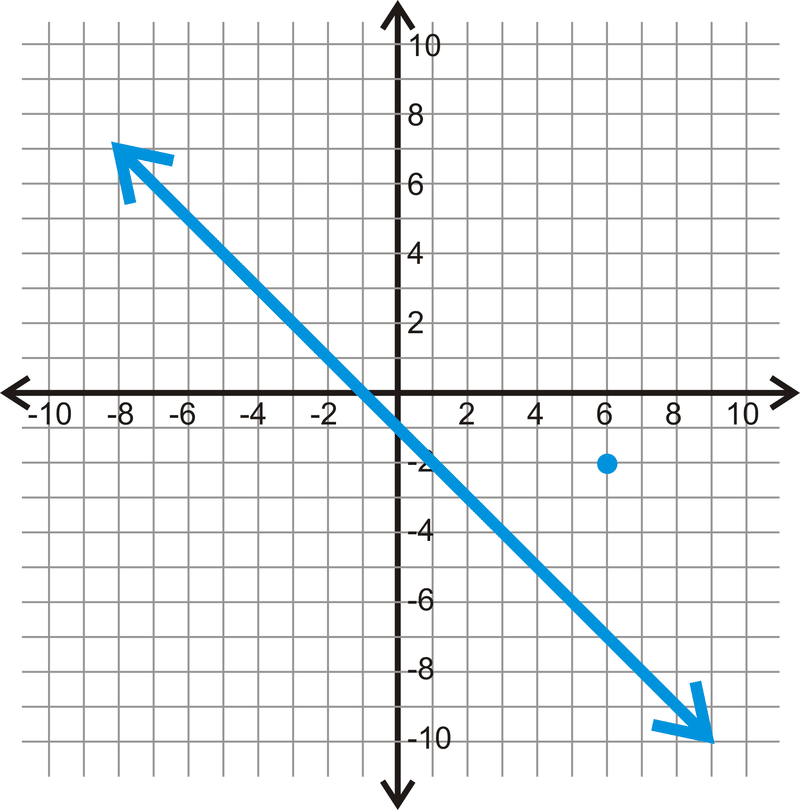
Малюнок\(\PageIndex{8}\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 3.8.

Лексика

Термін	Визначення
Паралельний	Дві або більше ліній паралельні, коли вони лежать в одній площині і ніколи не перетинаються. Ці лінії завжди будуть мати однаковий ухил.

Додатковий ресурс

Інтерактивний елемент

Відео: Рівняння паралельних і перпендикулярних ліній

Діяльність: Паралельні лінії в координатній площині дискусійні питання

Навчальні посібники: Лінії в координатній площині

Практика: Паралельні лінії в координатній площині

Реальний світ: Паралельні лінії в площині координат