Skip to main content
LibreTexts - Ukrayinska

3.5: Альтернативні внутрішні кути

  1. Last updated
  2. Save as PDF
  • Page ID
    54553

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Кути з протилежних сторін поперечні, але всередині ліній він перетинається.

    Альтернативні внутрішні кути - це два кути, які знаходяться на внутрішній частині\(l\) і\(m\), але з протилежних сторін поперечного.

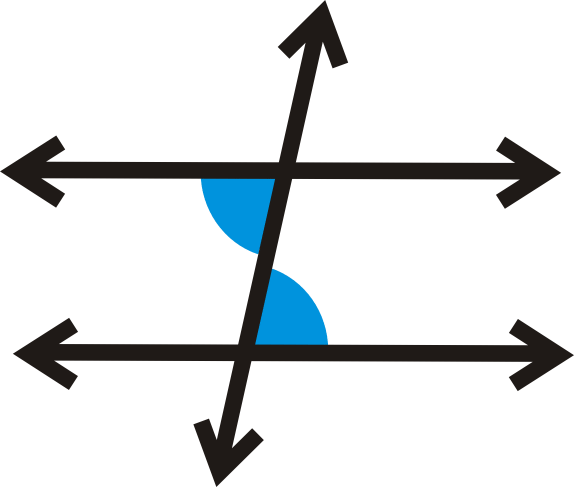
    Ф-Д_Б313250 ДБ66 ФК 135445ЕД 3ДД3С50506С7Д5БФ3БФ0ББ904D13E994+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Теорема про альтернативні внутрішні кути: Якщо дві паралельні лінії розрізаються поперечним, то альтернативні внутрішні кути є конгруентними.

    F-д_а3314ф04C041C4E7cd77c12a9 Дадек 3926Б523462 Деб 2726D9C47A+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Якщо\(l\parallel m\), то\(\angle 1\cong \angle 2\)

    Зворотна теорема про альтернативні внутрішні кути: Якщо дві лінії розрізаються поперечним, а альтернативні внутрішні кути конгруентні, то лінії паралельні.

    Якщо

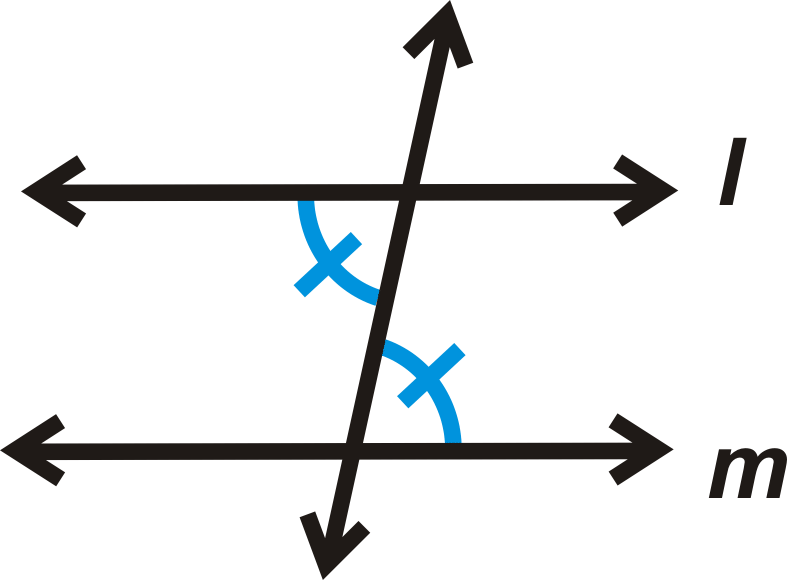
    F-D_7 АЦ3Б2Е74ФЦ08БА 224А323728ЕФ32ДЦА9Ф0Б0042ФК 18750610E3C4+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    потім\(l\parallel m\).

    Що робити, якщо вам представили два кути, які знаходяться на внутрішній стороні двох паралельних ліній, розрізаних поперечним, але з протилежних сторін поперечного? Як би ви описали ці кути і що ви могли б зробити висновок про їх заходи?

    Для Приклади\(\PageIndex{1}\) і\(\PageIndex{2}\), використовуйте надану інформацію, щоб визначити, які лінії паралельні. Якщо таких немає, напишіть none. Розглянемо кожне питання індивідуально.

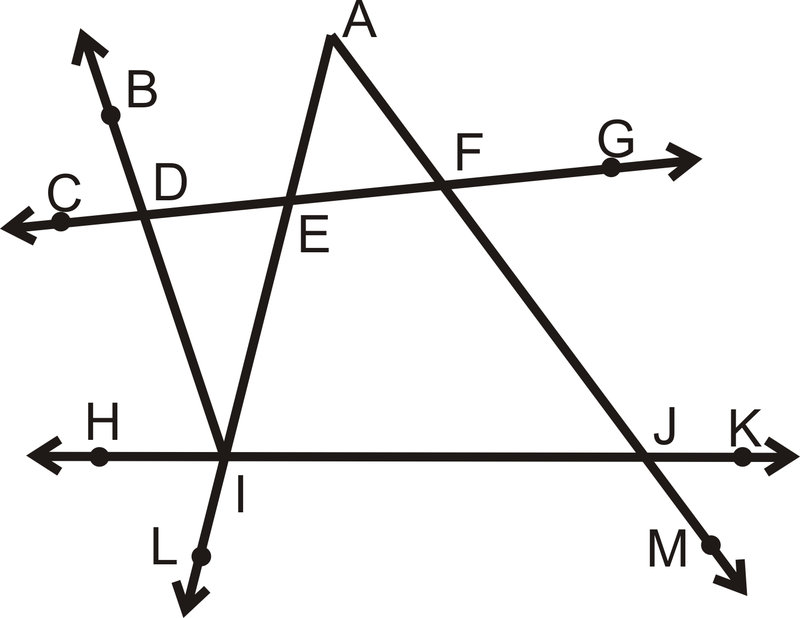
    F-д_А9669Д1041Ф370E9E54907Е 878108А838Д6CF9377D8D1F8AAC5A10+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Приклад\(\PageIndex{1}\)

    \(\angle EAF\cong \angle FJI\)

    Рішення

    Жоден

    Приклад\(\PageIndex{2}\)

    \(\angle EFJ\cong \angle FJK\)

    Рішення

    \(\overleftarrow{CG} \parallel \overleftarrow{HK}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть значення\(x\).

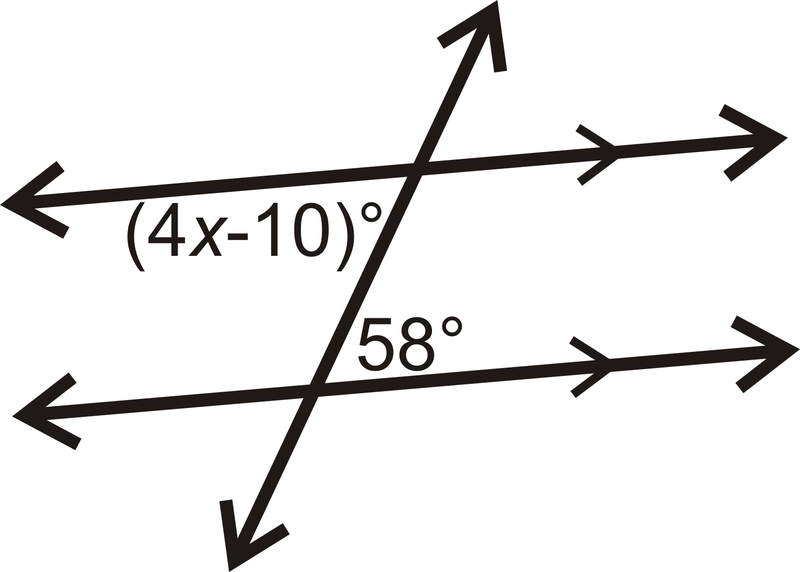
    Ф-Д_КА 38 АБ0710Д052576ДД2Ф77А 26С9ДБД 478Ф26ФЕ 51964CFE9E67C547C+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Два задані кути є чергуються внутрішніми кутами і рівними.

    \(\begin{align*} (4x−10)^{\circ} &=58^{\circ}\\ 4x &=68 \\ x &=17 \end{align*}\)

    Приклад\(\PageIndex{4}\)

    Правда чи помилково: альтернативні внутрішні кути завжди конгруентні.

    Рішення

    Це твердження є помилковим, але є поширеною помилкою. Пам'ятайте, що альтернативні внутрішні кути конгруентні лише тоді, коли лінії паралельні.

    Приклад\(\PageIndex{5}\)

    Кути чергуються внутрішніми кутами, і повинні бути рівні для\(a\parallel b\). Встановіть вирази рівні один одному і вирішуйте.

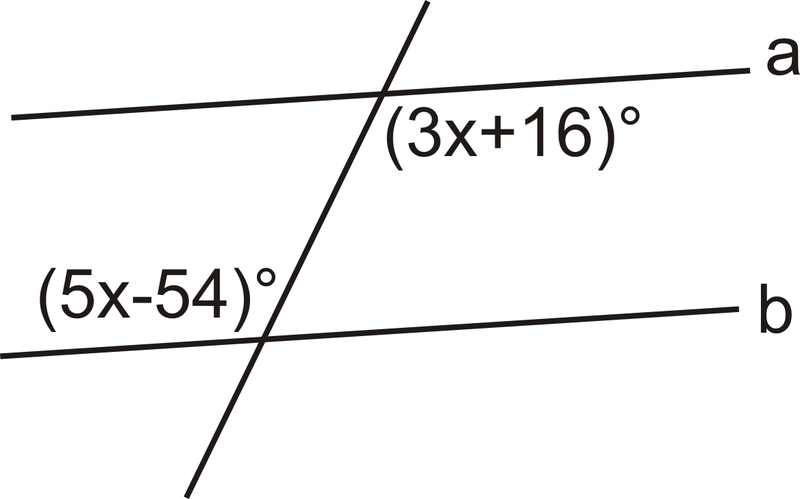
    F-D_284856552 БК 18ЕД 1А7273ДА249дБ Б Б Б. 18087 БКС5Б077АЕ 5AD4BB13D5+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    \(\begin{align*} 3x+16^{\circ} &=5x−54^{\circ} \\ 70&=2x \\ 35 &=x\end{align*}\)

    Щоб зробити\(a\parallel b\),\(x=35\).

    Рецензія

    1. Кутова пара\(\angle 6\) і\(\angle 3\) конгруентна, додаткова чи ні?
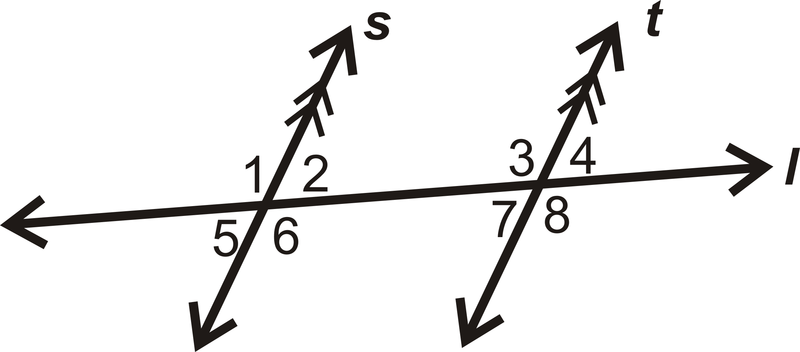
      F-D_C433 BBB 430C5A21 ЕФ 1034 Баабд 9 А175Е53Ф1Б202Б64С172D5+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
    2. Наведіть два приклади чергування внутрішніх кутів на схемі:
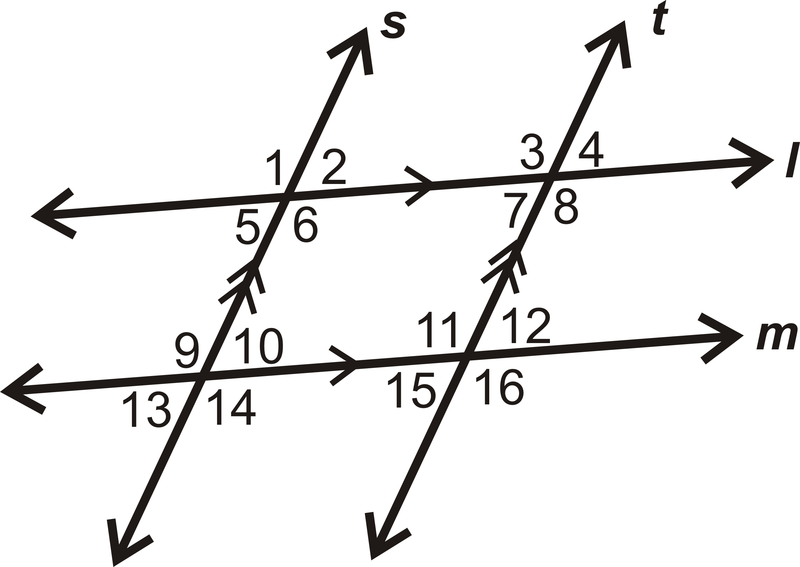
      F-D_ACF 685Ф70 АЦ87Б4075812Б7 ЕЦС 116ДБ Б ААК 3970Ф8ЕД 695303C88B+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)

    За 3-4 знайдіть значення\(x\).

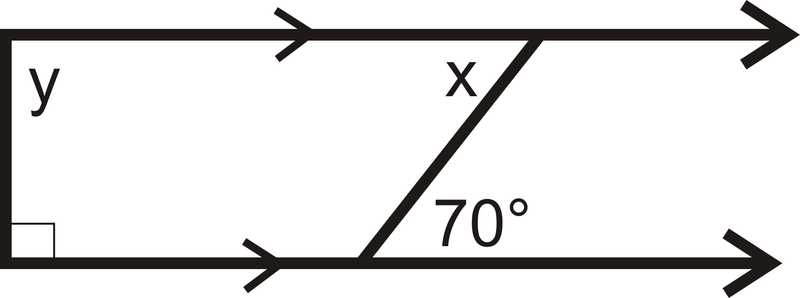    1. F-д_ЕФ9С9Е5Е1682147552С76009265Б7А902Б7А14102006 КБ31Б7352+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{9}\)
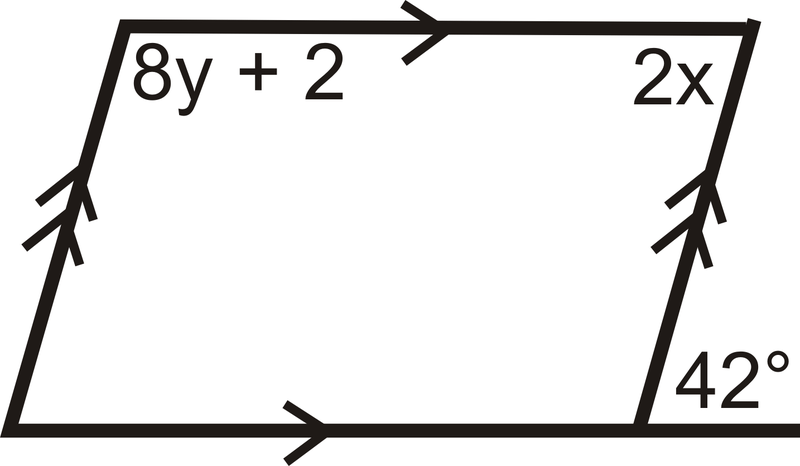    2. F-D_87a68f688 змінного струму 773c7556b7Fda4F683F42AAE988779A21D5A14F4B73+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{10}\)

    Для питання 5 скористайтеся зображенням нижче. Знайдіть значення\(x\).

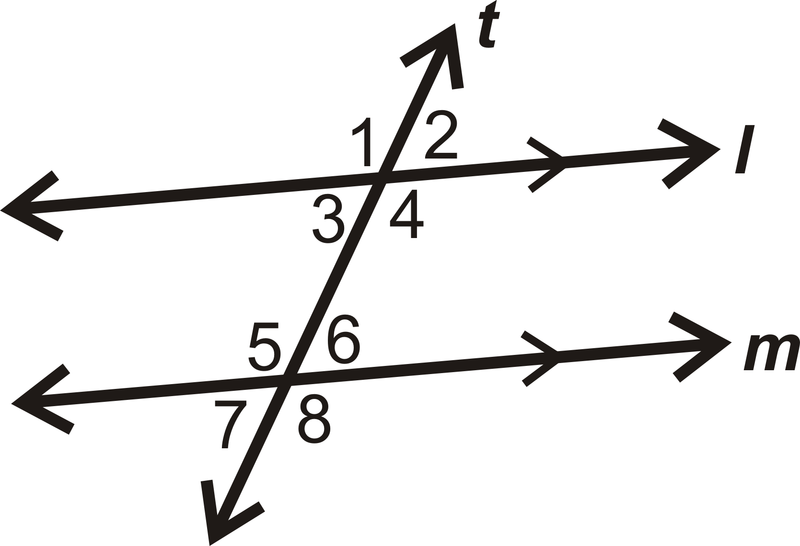
    F-д_7д690А17С6Б2Е3БК 2ЕС2070038 ЕД 705ЕБ9А6272064C8C84195102+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{11}\)
    1. \(m \angle 4=(5x−33)^{\circ}\),\(m \angle 5=(2x+60)^{\circ}\)
    1. Чи є лінії\(l\) і\(m\) паралельні? Якщо так, то звідки ви знаєте?
      F-D_3a6cd4f8211f54b79476e4ce493d6d6df493df49a9901f99dff35cbaa67+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{12}\)

    Для 7-10, яке значення\(x\) має бути, щоб лінії були паралельними?

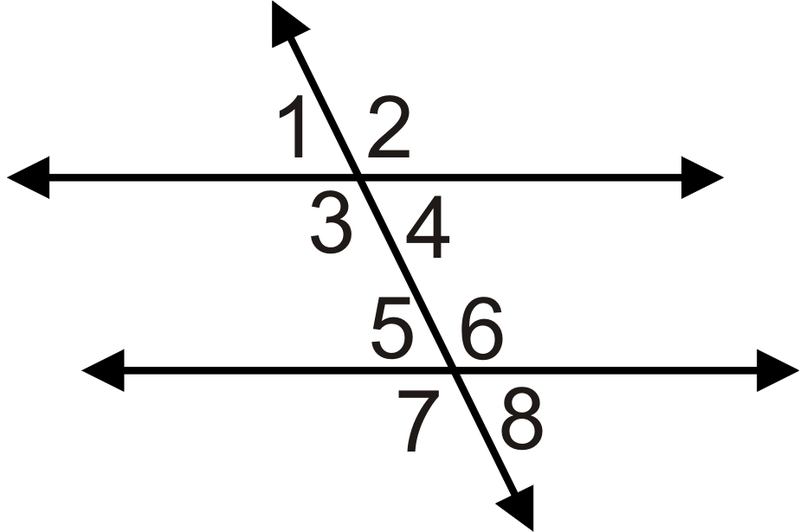
    F-д_963 дБД ФЧ7Б826Д8117ФФ8Ф1Ф6БФ93Е5С8Д514ФД8352Б7Б67+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{13}\)
    1. \(m \angle 4=(3x−7)^{\circ}\)і\(m \angle 5=(5x−21)^{\circ}\)
    2. \(m \angle 3=(2x−1)^{\circ}\)і\(m \angle 6=(4x−11)^{\circ}\)
    3. \(m \angle 3=(5x−2)^{\circ}\)і\(m \angle 6=(3x)^{\circ}\)
    4. \(m \angle 4=(x−7)^{\circ}\)і\(m \angle 5=(5x−31)^{\circ}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 3.4.

    Ресурси

    Лексика

    Термін Визначення
    чергувати внутрішні кути Чергуються внутрішні кути - це два кути, які знаходяться на внутрішній стороні двох різних ліній, але з протилежних сторін поперечної.
    альтернативні зовнішні кути Альтернативні зовнішні кути - це два кути, які знаходяться на зовнішній стороні двох різних ліній, але з протилежних сторін поперечної.

    Додаткові ресурси

    Відео: Альтернативні принципи внутрішніх кутів - основні

    Діяльність: Альтернативні внутрішні кути обговорення Питання

    Навчальні посібники: Кути та поперечні навчальні посібники

    Практика: Альтернативні внутрішні кути

    Реальний світ: альтернативні внутрішні кути