3.6: Альтернативні зовнішні кути

Last updated
Save as PDF

Page ID: 54554

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Кути з протилежних сторін поперечні, але поза лініями вона перетинається.

Альтернативні зовнішні кути - це два кути, які знаходяться на зовнішній\(m\) стороні\(l\) і, але з протилежних сторін поперечного.

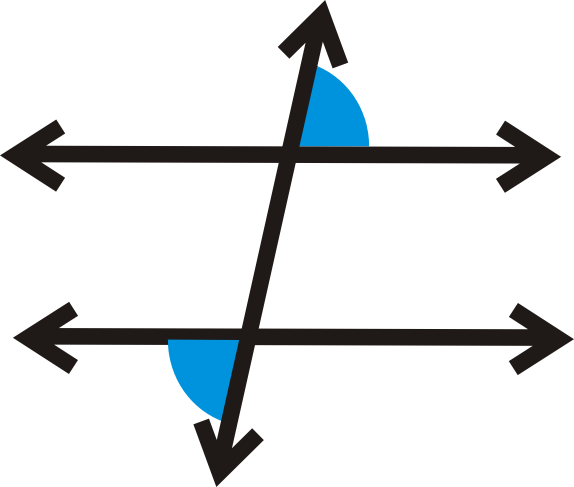
F-D_E0E1B24 Кабель 3907 ДБ79Е7Ф5А22391 DA41B338AC 18504818807D Плата 3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Теорема про альтернативні зовнішні кути: Якщо дві паралельні лінії розрізаються поперечним, то альтернативні зовнішні кути є конгруентними.

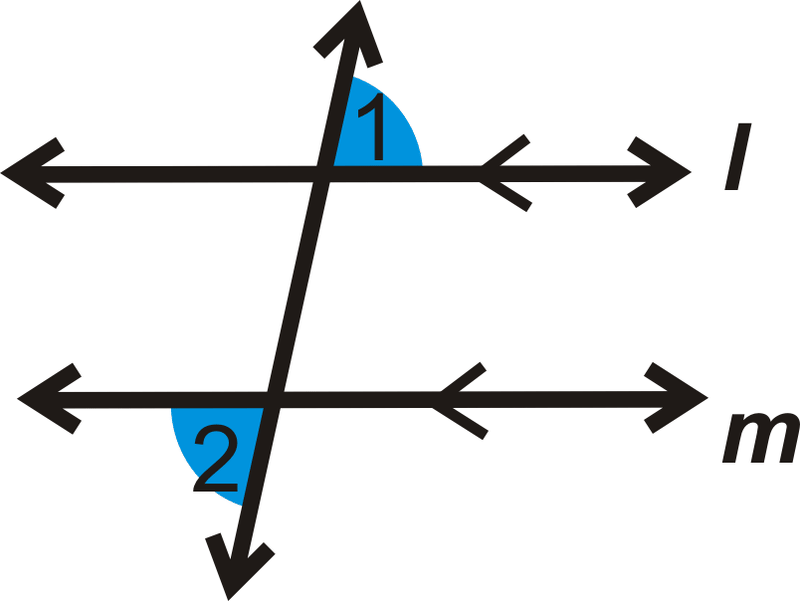
F-D_C0E 20623С4579 АБ6Д6ЦБА 701289С1С80107494240БА3825 ФКФА7 Додда+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Якщо\(l \parallel m\), то\(\angle 1\cong \angle 2\).

Конверс Теореми про альтернативні зовнішні кути: Якщо дві лінії розрізаються поперечним, а альтернативні зовнішні кути конгруентні, то лінії паралельні.

Якщо

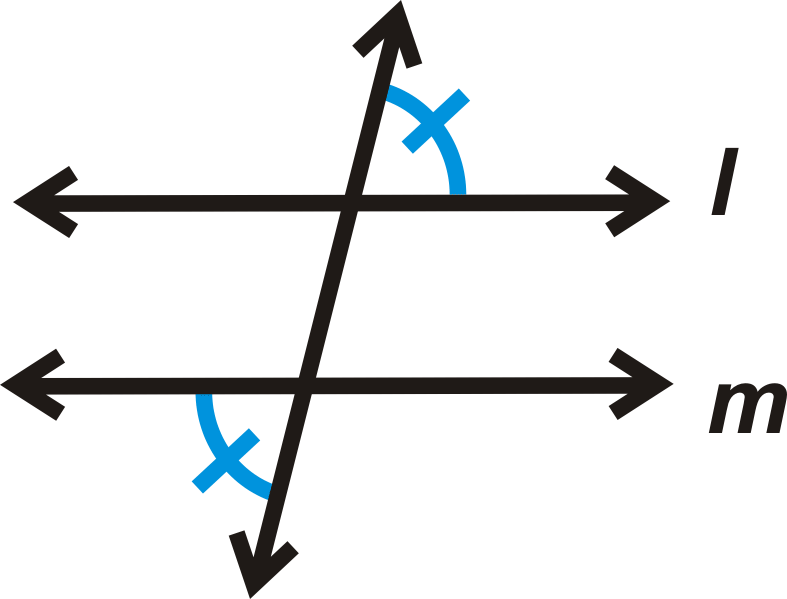
F-д_9С7ЕЦ17ФБ02А7141Е2063 ФД5 А712Ф254Б1356ЕБ99032E1F7C1B5905+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

потім\(l \parallel m\).

Що робити, якщо вам представили два кути, які знаходяться на зовнішній стороні двох паралельних ліній, розрізаних поперечним, але з протилежних сторін поперечного? Як би ви описали ці кути і що ви могли б зробити висновок про їх заходи?

Для Приклади\(\PageIndex{1}\) і\(\PageIndex{2}\), скористайтеся наступною схемою:

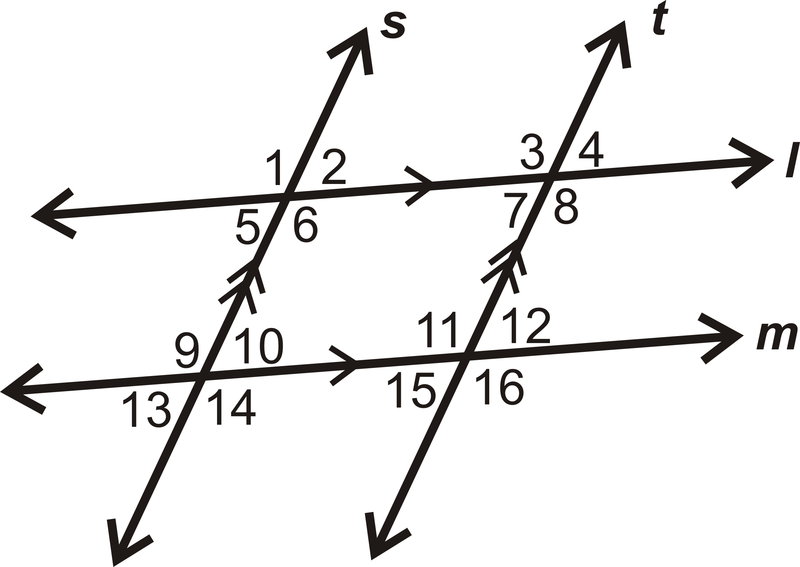
F-D_ACF 685Ф70 АЦ87Б4075812Б7 ЕЦС 116ДБ Б ААК 3970Ф8ЕД 695303C88B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Приклад\(\PageIndex{1}\)

Наведемо приклад пари чергуються зовнішніх кутів.

Рішення

\(\angle 1\)і\(\angle 14\) (багато інших можливостей)

Приклад\(\PageIndex{2}\)

Наведіть ще один приклад пари альтернативних зовнішніх кутів.

Рішення

\(\angle 2\)і\(\angle 13\) (багато інших можливостей, повинні відрізнятися від відповіді на приклад 1)

Приклад\(\PageIndex{3}\)

Знайдіть міру кожного кута і значення\) y\).

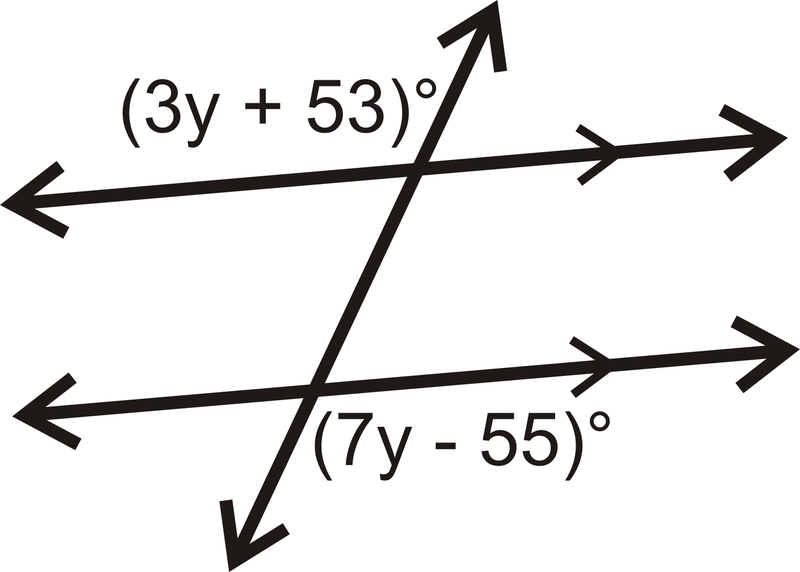
Ф-д_Б442 Ф21414Е3Д 898Б7С8А5109С44 Б344А3687Б10599412089 ED5B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

Кути є чергуються зовнішніми кутами. Оскільки лінії паралельні, кути рівні.

\(\begin{align*} (3y+53)^{\circ} &=(7y−55)^{\circ} \\ 108 &=4y \\ 27 &=y \end{align*}\)

Якщо\(y=27, then each angle is \([3(27)+53]^{\circ}=134^{\circ}\).

Приклад\(\PageIndex{4}\)

На карті нижче показані три дороги в місті Хуліо.

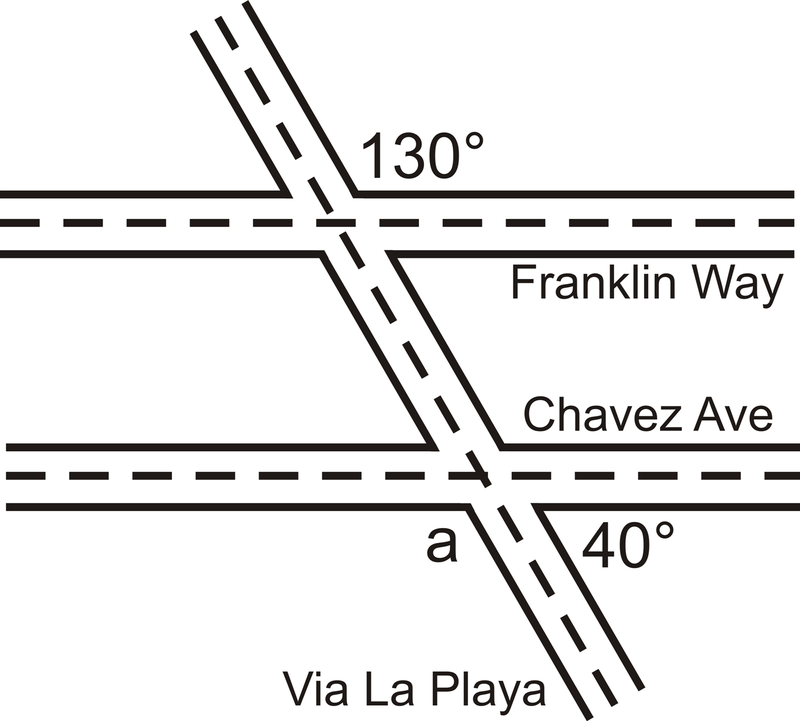
F-д_3Б7 ДБ739Ф102Б41478Б199Ф 5Е4Ф610 КБД 88018373E4D5CE6E85DC47+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Хуліо використовував геодезичний інструмент, щоб виміряти два кути на перехрестях на цьому малюнку, який він намалював (НЕ для масштабування). Хуліо хоче знати, чи паралельний Франклін Шей авеню Чавеса.

\(130^{\circ}\)Кут і\ кут a є альтернативними зовнішніми кутами. Якщо\(m \angle a=130^{\circ}\), то лінії паралельні.

\( \begin{align*} \angle a+40^{\circ} &=180^{\circ} & by\:the \:Linear \:Pair \:Postulate \\ \angle a&=140^{\circ} & \end{align*}\)

\(140^{\circ}\neq 130^{\circ}\), Тому Франклін Шей і Чавес-авеню не є паралельними вулицями.

Приклад\(\PageIndex{5}\)

Які лінії паралельні, якщо\(\angle AFG\cong \angle IJM\)?

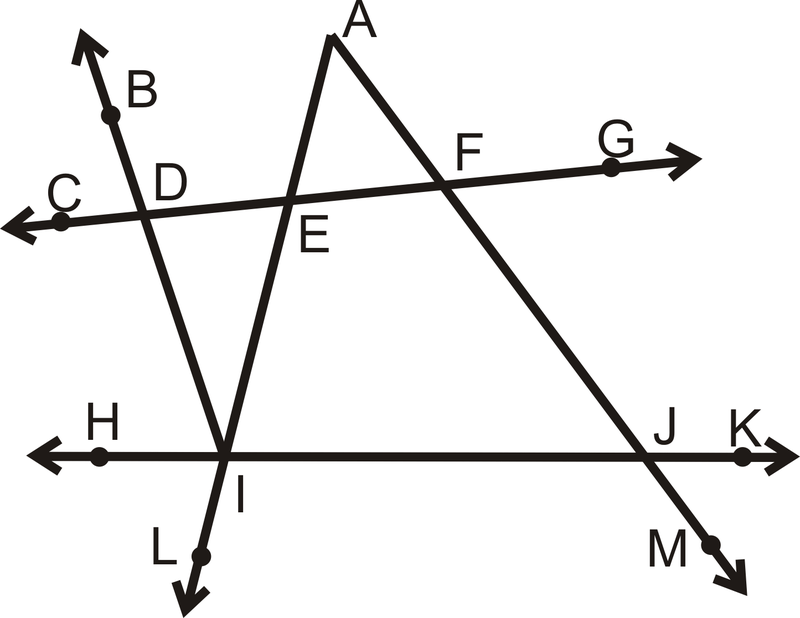
F-д_А9669Д1041Ф370E9E54907Е 878108А838Д6CF9377D8D1F8AAC5A10+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Рішення

Ці два кути є альтернативними зовнішніми кутами, тому якщо вони конгруентні, це означає, що\(\overleftrightarrow{CG}\parallel \overleftrightarrow{HK}\).

Рецензія

Знайдіть значення\(x\) if\(m \angle 1=(4x+35)^{\circ}\),\(m \angle8=(7x−40)^{\circ}\):

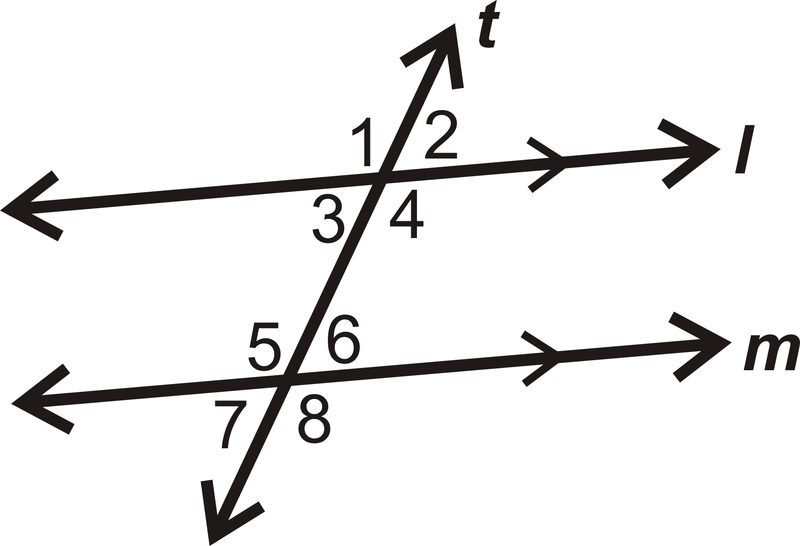
Малюнок\(\PageIndex{8}\)
Чи паралельні лінії 1 і 2? Чому чи чому ні?

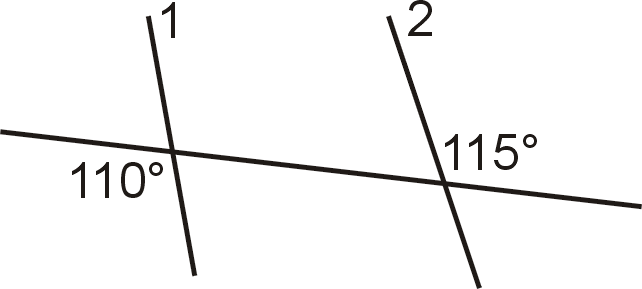
Малюнок\(\PageIndex{9}\)

Для 3-6, яке значення\(x\) має бути, щоб зробити лінії паралельними?

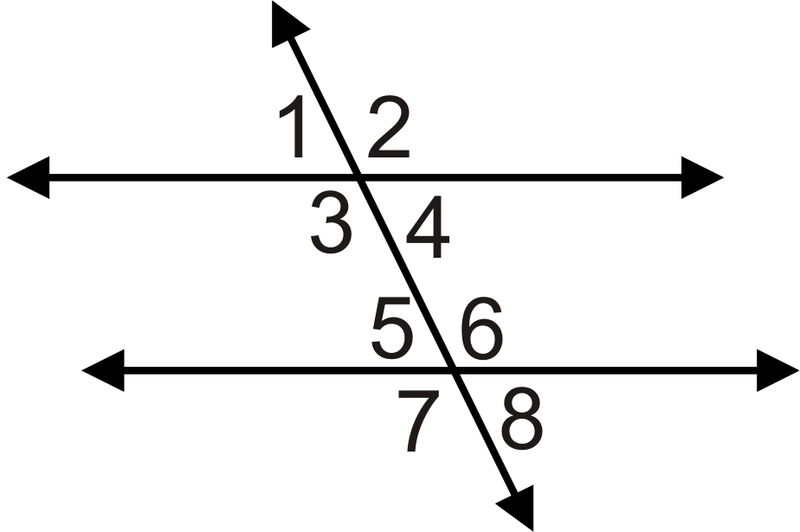
F-д_963 дБД ФЧ7Б826Д8117ФФ8Ф1Ф6БФ93Е5С8Д514ФД8352Б7Б67+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

\(m \angle2=(8x)^{\circ}\)і\(m \angle7=(11x−36)^{\circ}\)
\(m \angle1=(3x+5)^{\circ}\)і\(m \angle8=(4x−3)^{\circ}\)
\(m \angle2=(6x−4)^{\circ}\)і\(m \angle7=(5x+10)^{\circ}\)
\(m \angle1=(2x−5)^{\circ}\)і\(m \angle8=(x)^{\circ}\)

За 7-10 визначте, чи є твердження істинним або хибним.

Альтернативні зовнішні кути завжди конгруентні.
Якщо альтернативні зовнішні кути конгруентні, то лінії паралельні.
Альтернативні зовнішні кути знаходяться на внутрішній стороні з двох ліній.
Чергуються зовнішні кути знаходяться на протилежних сторонам поперечного.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 3.5.

Ресурси

Лексика

Термін	Визначення
альтернативні зовнішні кути	Альтернативні зовнішні кути - це два кути, які знаходяться на зовнішній стороні двох різних ліній, але з протилежних сторін поперечної.

Додатковий ресурс

Інтерактивний елемент

Відео: Альтернативні принципи зовнішніх кутів - основні

Діяльність: Альтернативні зовнішні кути обговорення Питання

Навчальні посібники: Кути та поперечні навчальні посібники

Практика: Альтернативні зовнішні кути

Реальний світ: альтернативні зовнішні кути