3.4: Відповідні кути

Last updated
Save as PDF

Page ID: 54561

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Визначте відповідні кути як відповідні кути.

Відповідні кути - це два кути, які знаходяться в «одному місці» щодо поперечного, але на різних лініях. Уявіть собі ковзання чотирьох кутів, утворених лінією\(l\) вниз до лінії\(m\). Кути, які збігаються, відповідають.

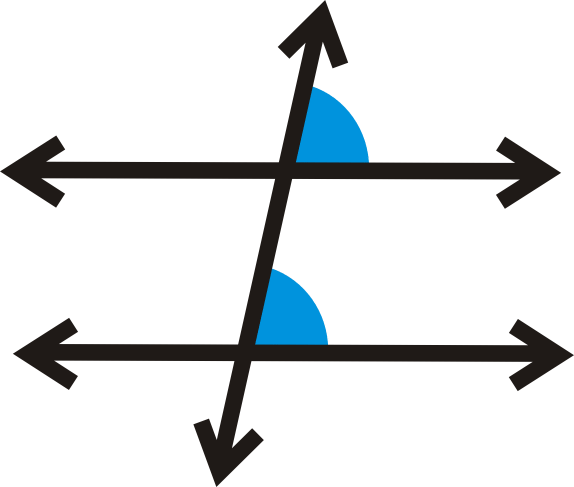
F-д_Е4 АФ 34д1Б0947 ЕС9Е0С6Е5Д81Д69Д25Е8Е33ФДДДД2Б11087Ф8241D5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Відповідні кути постулат: Якщо дві паралельні лінії розрізані поперечною, то відповідні кути є конгруентними.

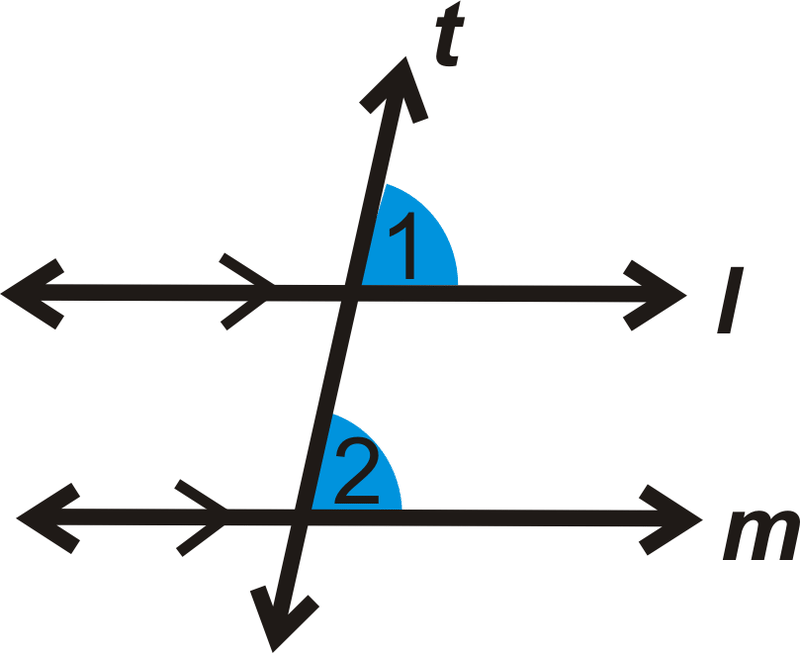
Ф-д_5СБ 183Ф69057304Б506С6Ф83Е8А129 ДЕФА 8Ф490Д1406072ДФ9504ДФ+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Якщо\(l \parallel m\), то\(\angle 1\cong \angle 2\).

Конверс відповідних кутів постулат: Якщо відповідні кути конгруентні, коли дві лінії розрізаються поперечним, то лінії паралельні.

Якщо

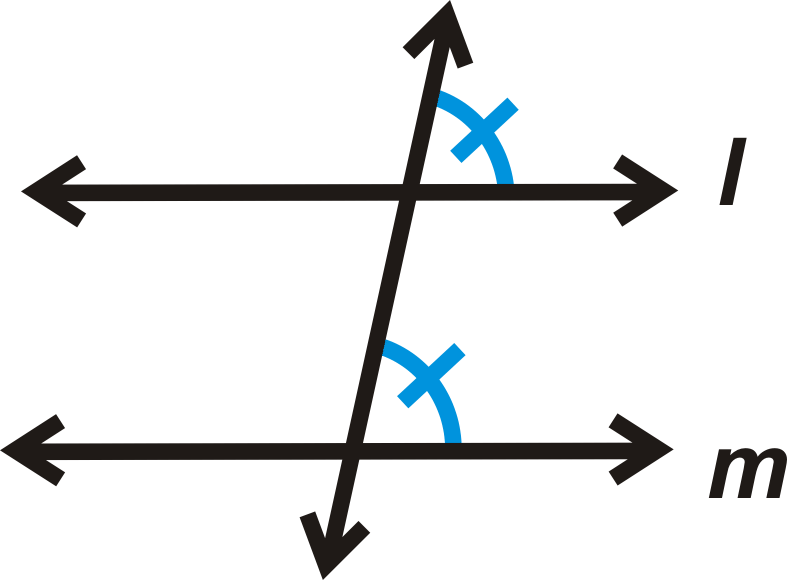
F-D_E07B6E10 CF346793А9А35 ДБ Б Б Б 1С31761 С Кабіна 2BA7990215A74CB801+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

потім\(l \parallel m\).

Що робити, якщо вам представили два кути, які знаходяться в одному місці щодо поперечного, але на різних лініях? Як би ви описали ці кути і що ви могли б зробити висновок про їх заходи?

Приклад\(\PageIndex{1}\)

Якщо\(m\angle 2=76^{\circ}\), що таке\(m\angle 6\)?

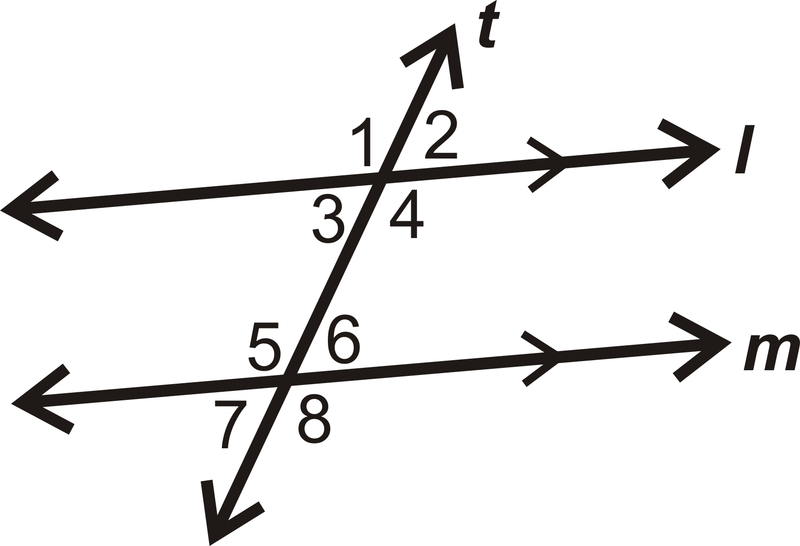
F-д_7д690А17С6Б2Е3БК 2ЕС2070038 ЕД 705ЕБ9А6272064С8С84195102+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

\(\angle 2\)і\(\angle 6\) відповідні кути і l||m від стрілок на малюнку. \(\angle 2\cong \angle 6\)Постулатом відповідних кутів, що означає, що\(m\angle 6=76^{\circ}\).

Приклад\(\PageIndex{2}\)

Використовуючи міри\ кут 2 та\ кут 6 з Прикладу 1, знайдіть всі інші заходи кута.

Рішення

Якщо\(m\angle 2=76^{\circ}\), то\(m\angle 1=180^{\circ}−76^{\circ}=104^{\circ}\) (лінійна пара). \ кут 3\ cong\ кут 2\) (вертикальні кути), так\(m\angle 3=76^{\circ}\). \(m\angle 4=104^{\circ}\)(вертикальний кут з\ кутом 1\)).

За Постулатом відповідних кутів ми знаємо\(\angle 1\cong \angle 5\)\(\angle 2\cong \angle 6\),\(\angle 3\cong \angle 7\),, і\(\angle 4\cong \angle 8\), так\(m\angle 5=104^{\circ}\)\(m\angle 6=76^{\circ}\),\(m\angle 7=76^{\circ}\), і\(m\angle 8=104^{\circ}\).

Приклад\(\PageIndex{3}\)

Знайдіть значення y:

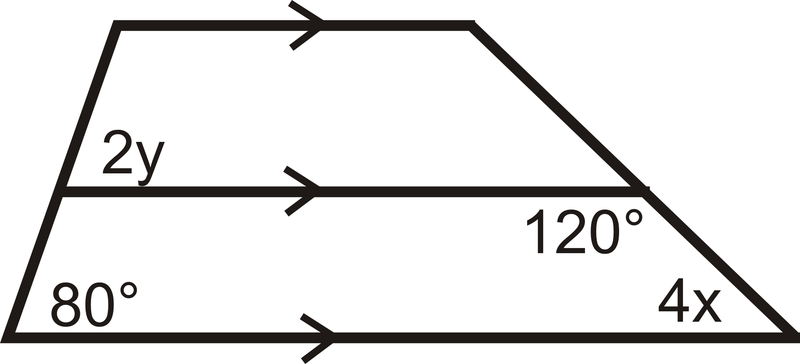
F-д_764c6382932c5ce076e8e9d394401386d1b5546376807aa3ce8FF988+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

Горизонтальні лінії позначені паралельно, а відмічений кут\(2y\) відповідає куту, позначеному 80, тому ці два кути є конгруентними. Це означає, що\(2y=80\) і тому\(y=40\).

Приклад\(\PageIndex{4}\)

Якщо a||b, які пари кутів конгруентні відповідним постулатом кутів?

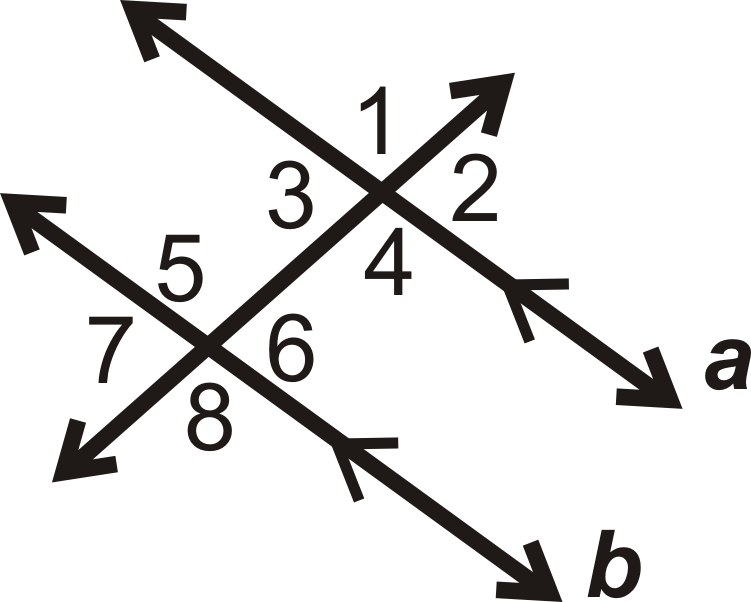
F-д_ДБ29Б4839Д72Е881911Е626Ф7Е7 АЦС836А573Е5Д9А558ЦАА288АА2885019+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Існує 4 пари конгруентних відповідних кутів:

\(\angle 1\cong \angle 5\),\(\angle 2\cong \angle 6\),\(\angle 3\cong \angle 7\), і\(\angle 4\cong \angle 8\).

Приклад\(\PageIndex{5}\)

Якщо\(m\angle 8=110^{\circ}\) і\(m\angle 4=110^{\circ}\), то що ми знаємо про лінії\(l\) і\(m\)?

Рішення

\(\angle 8\)і\(\angle 4\) є відповідними кутами. З тих пір\(m\angle 8=m\angle 4\), можна зробити висновок, що l||м.

Рецензія

Визначте, чи є кутова пара\(\angle 4\) і\(\angle 2\) є конгруентною, додатковою або ні:

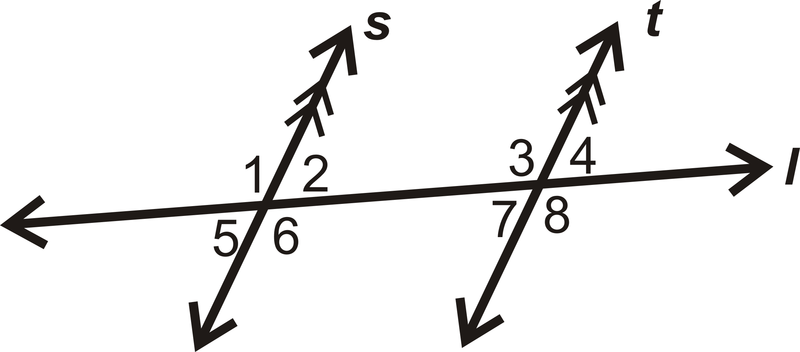
Малюнок\(\PageIndex{8}\)
Наведемо два приклади відповідних кутів на схемі:

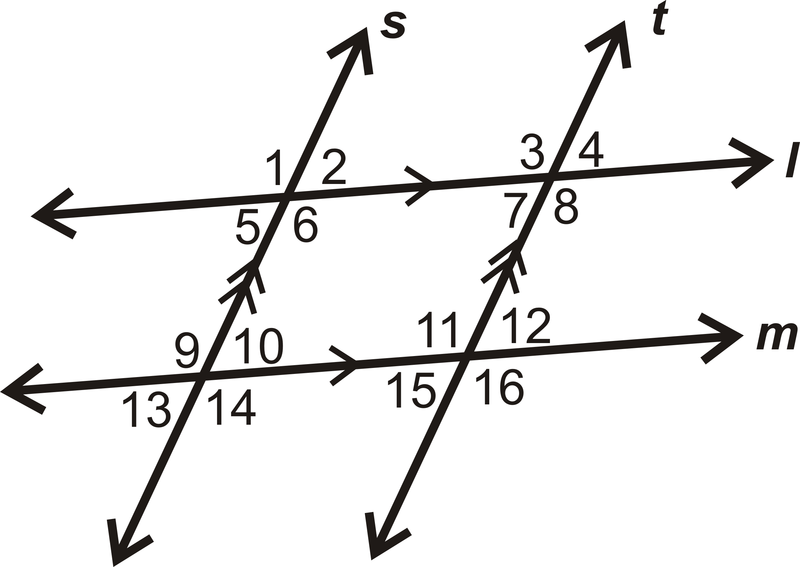
Малюнок\(\PageIndex{9}\)
Знайдіть значення\(x\):

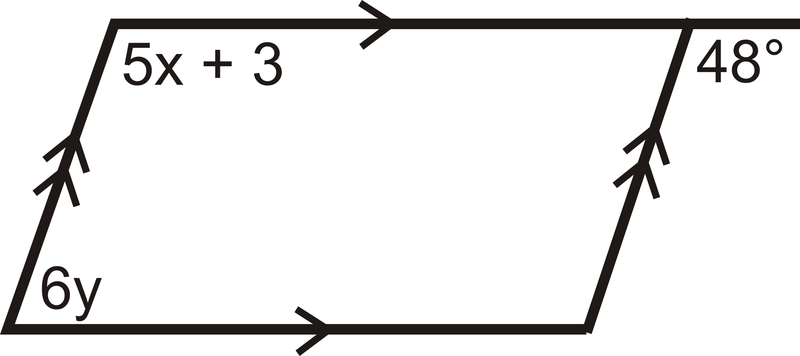
Малюнок\(\PageIndex{10}\)
Чи паралельні лінії? Чому чи чому ні?

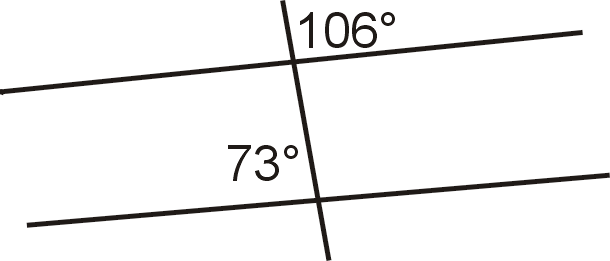
Малюнок\(\PageIndex{11}\)
Чи паралельні лінії? Обґрунтуйте свою відповідь.

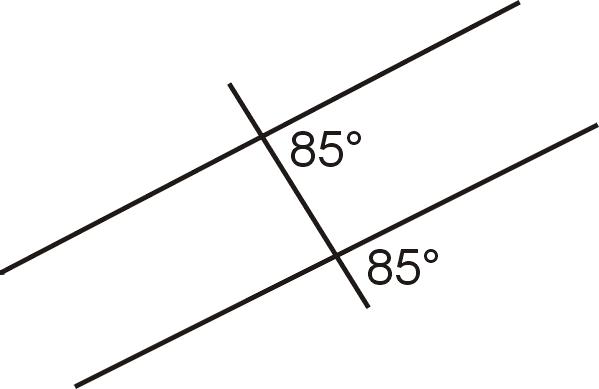
Малюнок\(\PageIndex{12}\)

Для 6-10, яке значення\(x\) має бути, щоб лінії були паралельними?

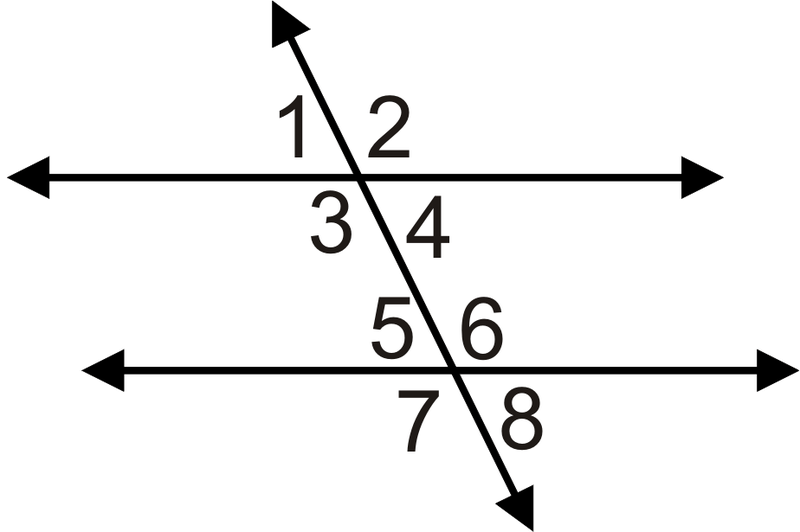
F-д_963 дБД ФЧ7Б826Д8117ФФ8Ф1Ф6БФ93Е5С8Д514ФД8352Б7Б67+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

Якщо\(m\angle 1=(6x−5)^{\circ}\) і\(m\angle 5=(5x+7)^{\circ}\).
Якщо\(m\angle 2=(3x−4)^{\circ}\) і\(m\angle 6=(4x−10)^{\circ}\).
Якщо\(m\angle 3=(7x−5)^{\circ}\) і\(m\angle 7=(5x+11)^{\circ}\).
Якщо\(m\angle 4=(5x−5)^{\circ}\) і\(m\angle 8=(3x+15)^{\circ}\).
Якщо\(m\angle 2=(2x+4)^{\circ}\) і\(m\angle 6=(5x−2)^{\circ}\).

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 3.3.

Ресурси

Лексика

Термін	Визначення
Відповідні кути	Відповідні кути - це два кути, які знаходяться в одному положенні щодо поперечного, але на різних лініях.

Додатковий ресурс

Інтерактивний елемент

Відео: Відповідні принципи кутів - основні

Діяльність: Відповідні кути дискусійні питання

Навчальні посібники: Кути та поперечні навчальні посібники

Практика: Відповідні кути

Реальний світ: відповідні кути