Skip to main content
LibreTexts - Ukrayinska

3.2: Паралельні та перекісні лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    54569

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Лінії, які ніколи не перетинаються.

    Паралельні лінії - це дві або більше ліній, які лежать в одній площині і ніколи не перетинаються. Щоб показати, що лінії паралельні, використовуються стрілки.

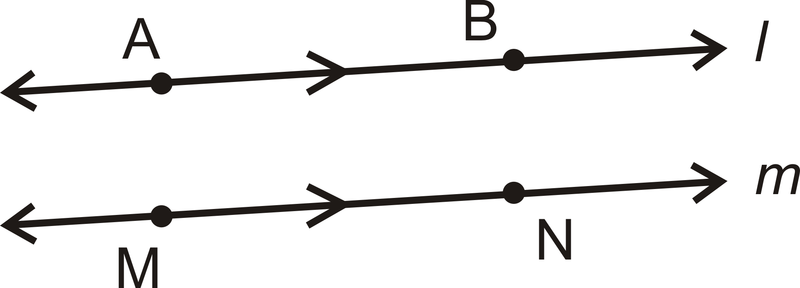
    Ф-д_АС 7АД 3БД 060БК 5А1566720Ф7168Д6Д 34Е96Ф798ДА02Е30Б68ADF654+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)
    Позначте це Скажи це
    \(\overleftrightarrow{AB} \parallel \overleftrightarrow{MN}\) \(AB\)Лінія паралельна лінії\(MN\)
    \(l\parallel m\) \(l\)Лінія паралельна лінії\(m\).

    У визначенні паралелі вживається слово «лінія». Однак відрізки ліній, промені і площини також можуть бути паралельними. На зображенні нижче показані дві паралельні площини з третьою синьою площиною, яка перпендикулярна обом з них.

    Ф-Д_5854С70С8С90Ф356282Е7А92Д61625096Е87Ф939АЕ22Ф3638Б65479+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{2}\)

    Перекісні лінії - це лінії, які знаходяться в різних площинях і ніколи не перетинаються. Вони відрізняються від паралельних ліній тим, що паралельні лінії лежать в одній площині. У кубі внизу\(\overline{AB}\) і\(\overline{FH}\) знаходяться косі і\(\overline{AC}\) і\(\overline{EF}\) перекіс.

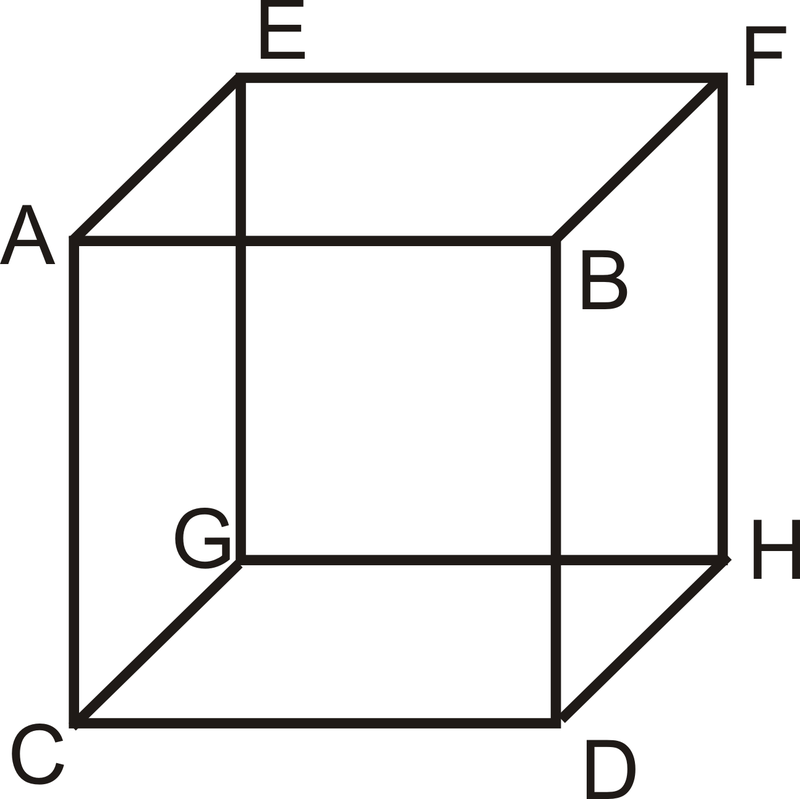
    F-д_Б159С6Д 3259B889853C4988A2E4А67659 Дед 45БА 0291F407C+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Основні факти про паралельні лінії

    Властивість: Якщо рядки\(l\parallel m\) і\(m\parallel n\), то\(l\parallel n\).

    Якщо

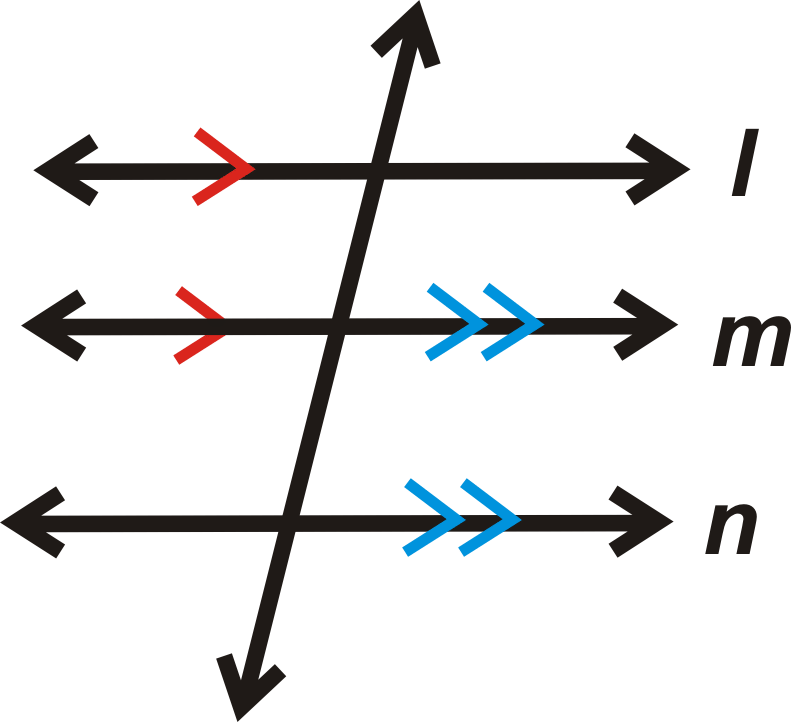
    F-D_597cd854A3F47509DA6A 94587202Е51Ф73БА3423305Е087Б258521Б6+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{4}\)

    потім

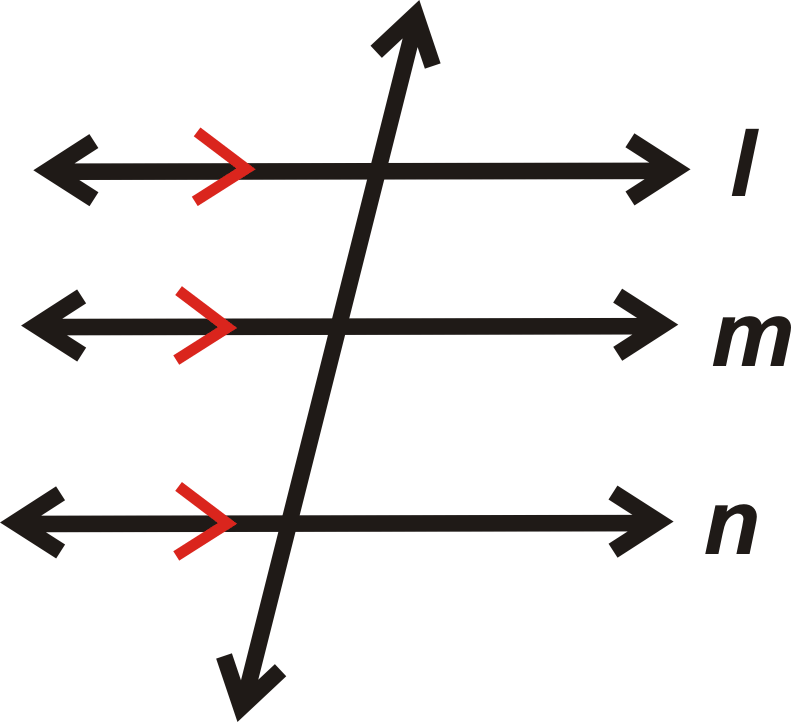
    F-D_11753 АД 9951Б0БД Д 902 АА6Б624969С5АЦ7Ф5КБ503Е1А6ФД5480+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

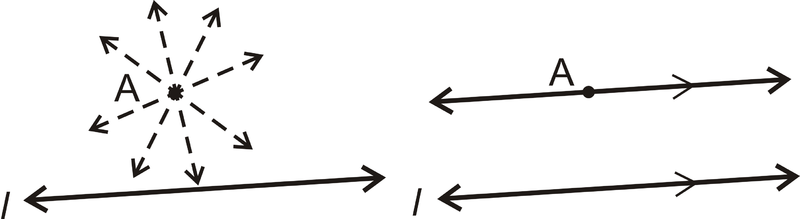
    Постулат: Для будь-якої лінії і точки, яка не знаходиться на лінії, є одна лінія, паралельна цій лінії через точку. Є нескінченно багато ліній, які проходять\(A\), але тільки одна, яка паралельна\(l\).

    Ф-Д_5 ББФ 12С25ЕБ806АФФА 8С35 ББ 55213204Е48080А66ЕБ74549 ББ32+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

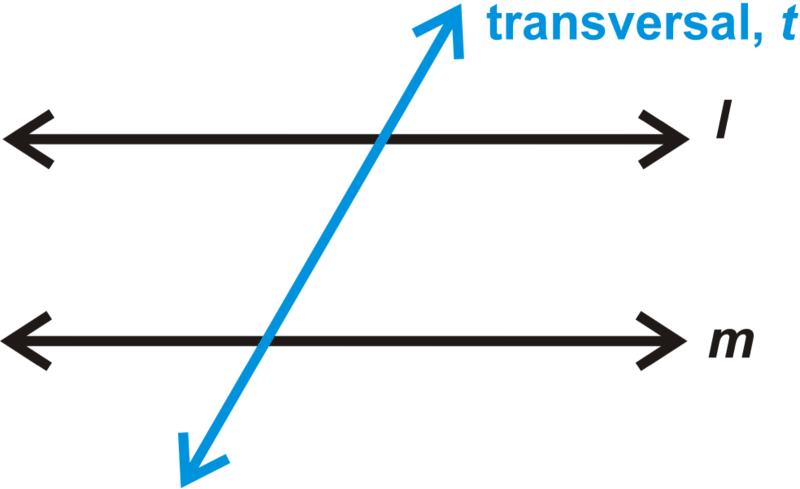
    Поперечний - це лінія, яка перетинає дві інші лінії. Площа між\(l\) і\(m\) є інтер'єром. Площа зовні\(l\) і\(m\) є зовнішнім.

    Ф-Д_Д358Е6Д2А627С53136 ЕФ5797 ДБ22СА4381А770965А986ЕФ75621780+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Що робити, якщо вам дали пару рядків, які ніколи не перетинаються і попросили описати їх? Яку термінологію ви б використали?

    Використовуйте малюнок нижче для Приклади\(\PageIndex{1}\) і\(\PageIndex{2}\). Два п'ятикутника паралельні і всі прямокутні сторони перпендикулярні обом.

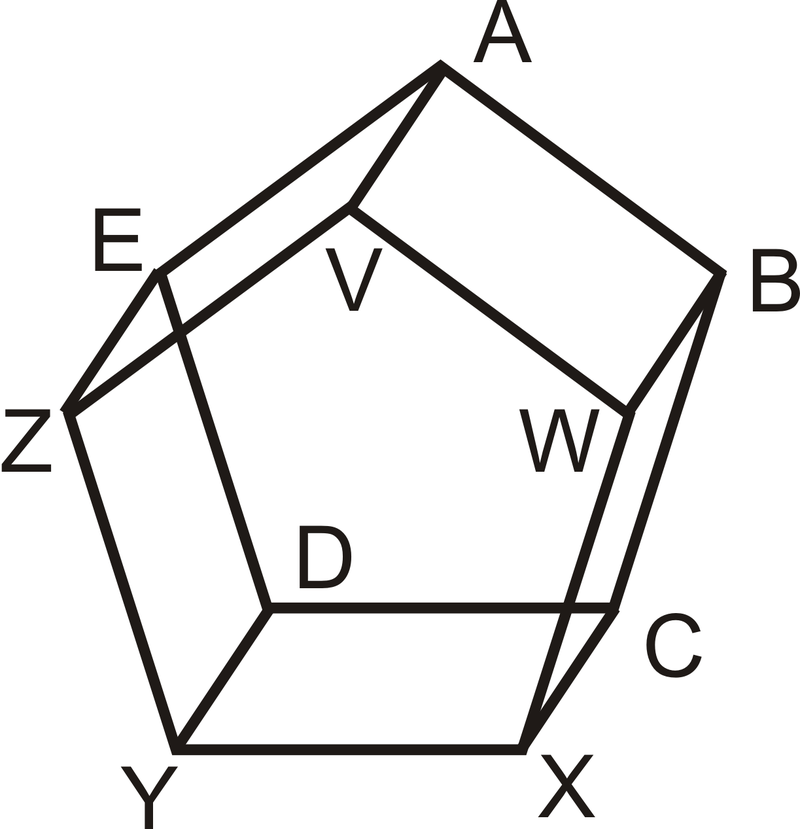
    Ф-Д_ДК 6 ліжко 64085Ф2А2Д510741341С01148Ф593А03С99081005265Ф67ЦЕ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Приклад\(\PageIndex{1}\)

    Знайдіть дві пари ліній перекісу.

    Рішення

    \(\overline{ZV}\)і\(\overline{WB}\). \(\overline{YD}\)і\(\overline{VW}\)

    Приклад\(\PageIndex{2}\)

    Бо\(\overline{XY}\), скільки паралельних ліній буде проходити через точку\(D\)? Назвіть цей/ці рядки.

    Рішення

    Один рядок,\(\overline{CD}\)

    Приклад\(\PageIndex{3}\)

    True або false: деякі пари ліній перекосу також паралельні.

    Рішення

    Це помилково, за визначенням косі лінії знаходяться в різних площинях, а паралельні лінії знаходяться в одній площині. Дві лінії можуть бути косими або паралельними (або ні), але ніколи обидві.

    Приклад\(\PageIndex{4}\)

    Використовуючи куб нижче, перерахуйте пару паралельних ліній.

    F-д_Б159С6Д 3259B889853C4988A2E4А67659 Дед 45БА 0291F407C+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

    Однією з можливих відповідей є рядки\(\overline{AB}\) і\(\overline{EF}\).

    Приклад\(\PageIndex{5}\)

    Використовуючи куб нижче, перерахуйте пару ліній перекосу.

    F-д_Б159С6Д 3259B889853C4988A2E4А67659 Дед 45БА 0291F407C+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)

    Рішення

    Однією з можливих відповідей є\(\overline{BD}\) і\(\overline{CG}\).

    Рецензія

    1. Який з наведених нижче є найкращим прикладом паралельних ліній?
      1. Залізничні колії
      2. Ліхтарний стовп і тротуар
      3. Довгота на глобусі
      4. Стоунхендж (кам'яна споруда в Шотландії)
    2. Який із наведених нижче є найкращим прикладом перекісних ліній?
      1. Дах будинку
      2. Північна автострада та шляхопровід на схід
      3. Довгота на глобусі
      4. Міст Золоті Ворота

    Використовуйте картинку нижче для питань 3-5.

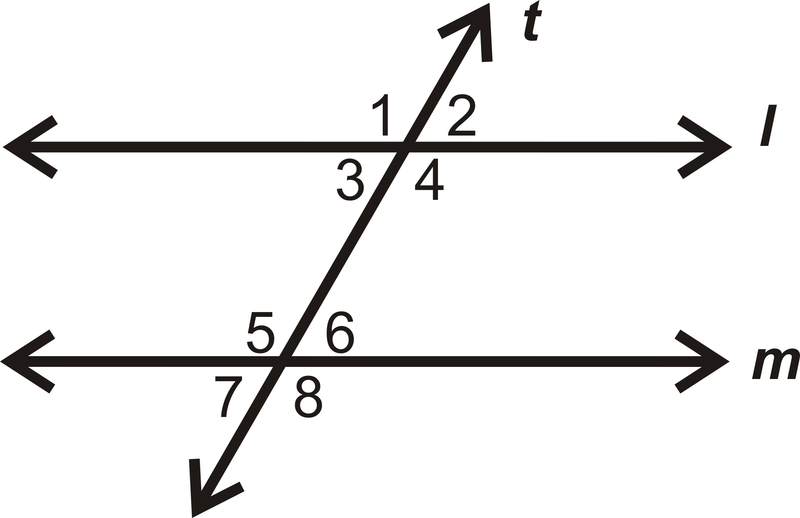
    \F-D_F8Е0Д0С765E41 БД04КА58А5Е73 КД09555А02А929Д06Ф952CF3E5DD7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{11}\)
    1. Якщо\(m\angle 2=55^{\circ}\), які ще ракурси ви знаєте?
    2. Якщо\(m\angle 5=123^{\circ}\), які ще ракурси ви знаєте?
    3. Є\(l\parallel m\)? Чому чи чому ні?

    За 6-10 визначте, чи є твердження істинним або хибним.

    1. Якщо\(p\parallel q \) і\(q\parallel r\), то\(p\parallel r\).
    2. Лінії перекісу ніколи не знаходяться в одній площині.
    3. Лінії перекісу можуть бути перпендикулярними.
    4. Площини можуть бути паралельними.
    5. Паралельні лінії ніколи не знаходяться в одній площині.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 3.1.

    Ресурси

    Лексика

    Термін Визначення
    паралельні лінії Дві або більше ліній, які лежать в одній площині і ніколи не перетинаються. Паралельні лінії завжди будуть мати однаковий ухил.
    Лінії перекісу Перекісні лінії - це лінії, які знаходяться в різних площинях і ніколи не перетинаються.
    поперечний Поперечний - це лінія, яка перетинає дві інші лінії.
    Паралельний Дві або більше ліній паралельні, коли вони лежать в одній площині і ніколи не перетинаються. Ці лінії завжди будуть мати однаковий ухил.
    Перекіс Перекіс заданого набору означає викликати тенденцію даних на користь того чи іншого кінця.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Доведення паралельних ліній

    Практика: Паралельні і перекіс лінії обговорення питання

    Навчальні посібники: Керівництво по вивченню ліній та кутів

    Практика: Паралельні та похилі лінії

    Реальний світ: Короткі замикання: як працюють паралельні схеми