Skip to main content
LibreTexts - Ukrayinska

1.18: Класифікувати багатокутники

  1. Last updated
  2. Save as PDF
  • Page ID
    54949

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Категорії багатокутників засновані на кількості сторін, а також від того, чи є вони увігнутими або опуклими.

    Багатокутники

    Багатокутник - це будь-яка замкнута двовимірна фігура, яка повністю складається з відрізків ліній, які перетинаються у своїх кінцевих точках. Багатокутники можуть мати будь-яку кількість сторін і кутів, але сторони ніколи не можуть бути вигнутими. Відрізки називаються сторонами багатокутників, а точки, де перетинаються сегменти, називаються вершинами.

    Багатокутники можуть бути як опуклими, так і увігнутими. Термін увігнутий відноситься до печери, або багатокутник - «спелеологія». Всі зірки є увігнутими багатокутниками.

    F-D_08547 AD14B4312AD7219A22F2371 ЕЕ358Е105Б0771Ф60Б9089002ДБ+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{1}\)

    Опуклий багатокутник не прогинається. Опуклі багатокутники виглядають так:

    F-д_99D 699C Плата за 7 АФ 2920А9 Ед Б 88F5E1A7860DA32E085A12C2EC0331+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{2}\)

    Діагональ - це небічний відрізок лінії, який з'єднує дві вершини опуклого багатокутника.

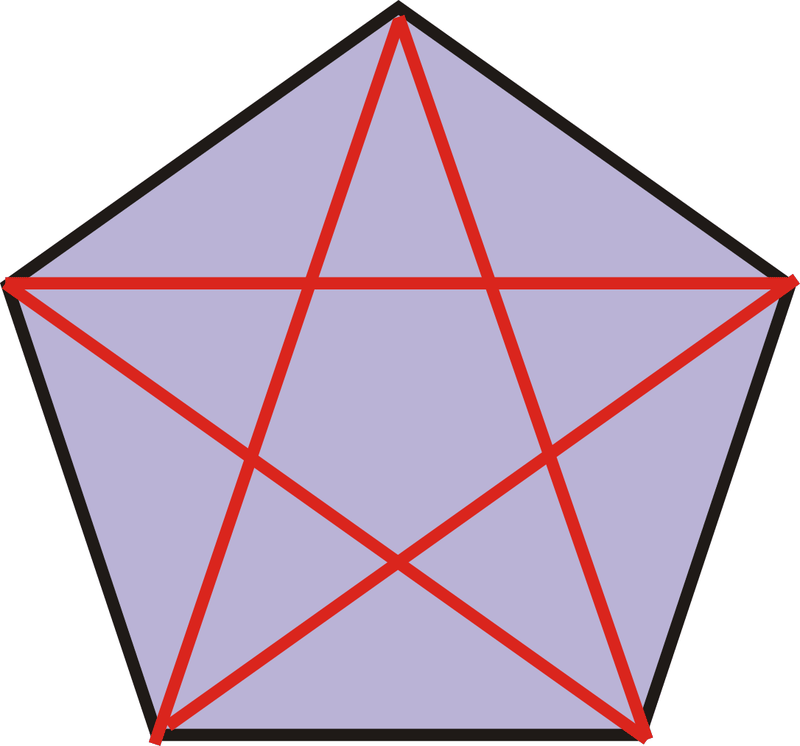    Ф-Д_28Д140ДД4Б8486606ЕД 1149D156396 CF1A4167D595116C235EBEB0B+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{3}\)

    Відрізки червоної лінії - це всі діагоналі. Цей п'ятикутник має 5 діагоналей.

    Незалежно від того, чи є багатокутник опуклим або увігнутим, він завжди називається за кількістю сторін. Дослідіть зв'язок між кількістю сторін опуклого багатокутника і його діагоналями. Чи можете ви заповнити таблицю?

    Назва багатокутника Кількість сторін Кількість діагоналей Опуклий приклад
    Трикутник 3 0
    F-D_A7361 ЕА 7Д99 ФАЕ5Б 32С7982ФКБ47А 8Д195С5ДФ Додати 7F6BE6670B8+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)
    Чотирикутник 4 2
    F-д_Е7 ЕБЕ1078E4Dcd 66Ф1732616266Е935кД001Ф2Б6308C9C7C33E5038D+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{5}\)
    Пентагон 5 5
    F-д_Ф 470С8440АБ02Е5А9910447 АБК 4Е677Б73КС24Е02БД304740Ф112Ф12+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{6}\)
    Шестигранник 6 9
    F-D_918 ББ 79593E3E3E67094890 Де9С57СЕ 170А5А5АЕ 807666C865E69FC5AD4+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{7}\)
    Гептагон 7 ?
    Ф-Д_Ф2Е44Е43А808С45БФ 53 АБД 09726БА51087 Додати 3e02d83204 ліжко 54АФБ+зображення_крихіткий+зображення_крихітка_крихітка_pngМалюнок\(\PageIndex{8}\)
    Восьмикутник 8 ?
    Ф-Д_6Ф2465Е95С9С1Е60А8Б9Д0КФ4Е7А5325846704А22781D3B1DFC 3299+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{9}\)
    Нонагон 9 ?
    F-д_366Ф4С4А918583C11CF+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{10}\)
    Декагон 10 ?
    F-д_7Ф6561С94ДБ6Б38С2Ф7Б30919 С9АФ1БД ДЭ664Б3А1С312825CEE31666+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{11}\)
    Ундекагон або хендекагон 11 ?
    F-д_3834Б4А1ААЕ 5213Е8Б4 Фе 286Ф79С7Б46Б6ФЕ438Ф123Д3Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6Б6БМалюнок\(\PageIndex{12}\)
    Додекагон 12 ?
    F-D_090344F8 Додати 7FCE617 ББ 34Е5365ЕД4 ФС2 ФБДБА 583 БК2 ЕЕ7686БА37+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{13}\)
    n-кутник n (де n> 12) ?
    Ф-д_д0фа3Е86Е84Б0916Ф70С063А8С7Е6А0Ф42Е5ДА 1836114Б79Е80Б8+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{14}\)

    Що робити, якщо вам сказали, скільки сторін має багатокутник? Як би ви описали багатокутник на основі цієї інформації?

    Приклад\(\PageIndex{1}\)

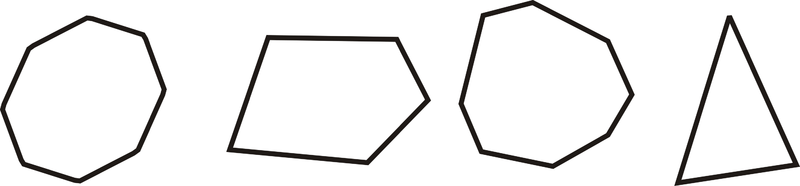
    Яка з наведених нижче фігур є багатокутником?

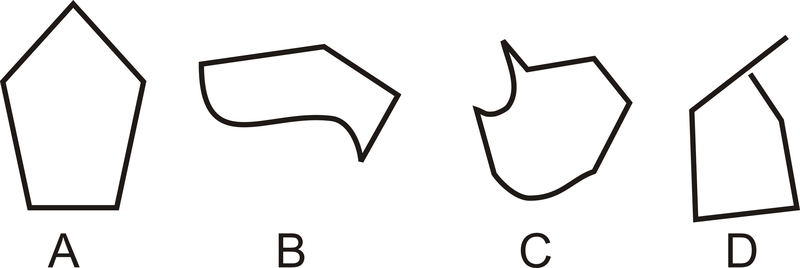    F-д_Д9АФ92Ф7000 ЕКА 96Б68ЕДА 41 БЕ103120812788210А125ЕБ6ДДЕ2E0+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{15}\)

    Рішення

    Найпростіший спосіб ідентифікувати багатокутник - визначити, які фігури не є багатокутниками. B і C мають принаймні одну вигнуту сторону, тому вони не є багатокутниками. D має всі прямі сторони, але одна з вершин знаходиться не в кінцевій точці, тому вона не є багатокутником. A - єдиний багатокутник.

    Приклад\(\PageIndex{2}\)

    Визначте, чи є наведені нижче форми опуклими або увігнутими.

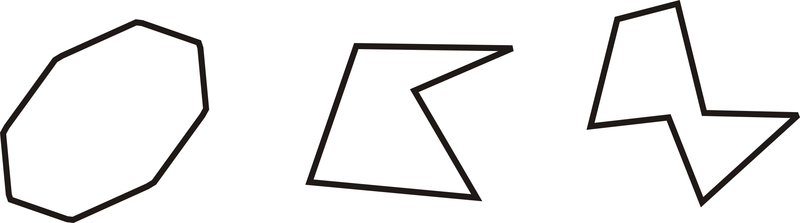    Ф-Д_8АА7Б9671 С8Д 8АД 259230009578225БФ Ф 60С7С1Ф4Е09050Б8633Б733+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{16}\)

    Рішення

    Щоб побачити, чи є багатокутник увігнутим, подивіться на багатокутники і подивіться, чи будь-який кут «печери» до внутрішньої частини багатокутника. Перший багатокутник цього не робить, тому він опуклий. Два інших роблять, тому вони увігнуті.

    Приклад\(\PageIndex{3}\)

    Назвіть три багатокутники нижче за кількістю сторін і якщо він опуклий або увігнутий.

    F-д_Ф2ЕД 10682 СА278009С4Д 54 CEED 2709Ф81С8559Д374611731552945+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{17}\)

    Рішення

    Рожевий багатокутник - увігнутий шестикутник (6 сторін).

    Зелений багатокутник опуклий п'ятикутник (5 сторін).

    Жовтий багатокутник являє собою опуклий декагон (10 сторін).

    Приклад\(\PageIndex{4}\)

    Намалюйте 7-сторонній багатокутник, який також називають гептагоном. Скільки діагоналей має гептагон?

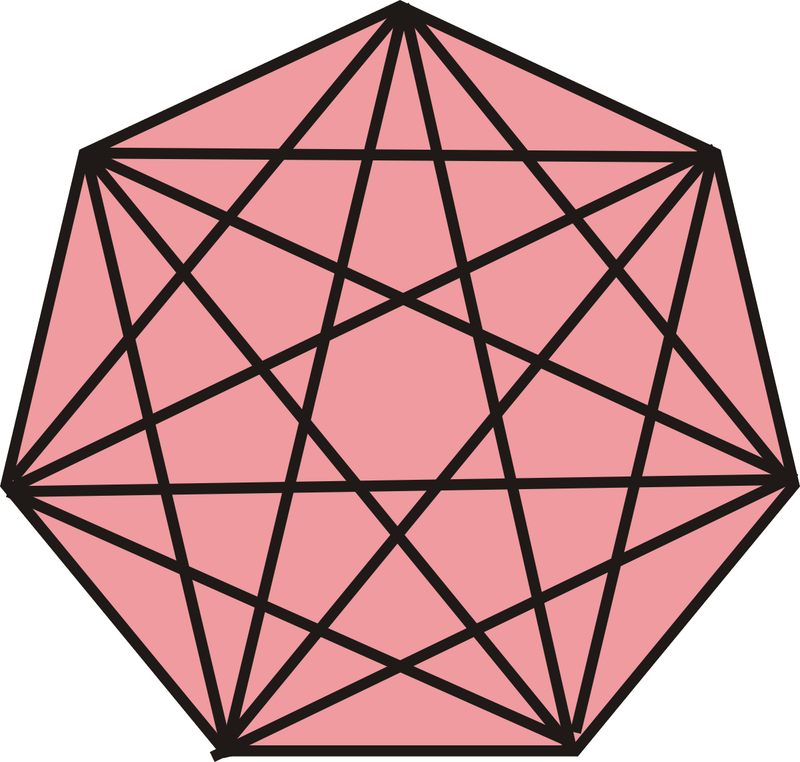    F-д_10173 АА0021СДБ 631571С62ДА3 АА7673 ЕФ8 ФАЕ99Е1БДД1А3Ф16Д38+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{18}\)

    Рішення

    Спочатку намалюйте гептагон. Намалювавши всі діагоналі і порахувавши їх, бачимо їх 14.

    Приклад\(\PageIndex{5}\)

    True або false: Чотирикутник - це завжди квадрат.

    Рішення

    Помилкові. Тільки чотирикутники з чотирма конгруентними сторонами і чотирма прямими кутами будуть квадратами. Існує багато чотирикутників (таких як прямокутники, повітряні змії, паралелограми, трапеції тощо), які не обов'язково є квадратами.

    Рецензія

    У задачах 1-6 назвіть кожен багатокутник якомога докладніше.

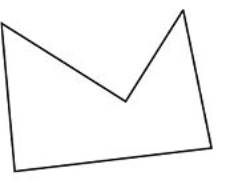    1. Ф-Д_9Ф03С48Е12197E341DA17B38C2А05Е1А17Ф86C1DCFB352958+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{19}\)
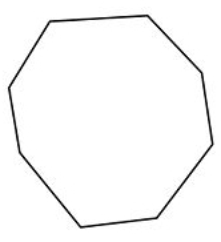    2. Ф-д_4кд 20е 36028АААФ 01697 АЦ0Е50ФЕ41870Б5Ф6Ф66Ф3888Д83156ДДДБ+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{20}\)
    3. F-д_176d0e79e82461e06d74059951647d1 САД 58БД45089Ф11Б600А930+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{21}\)
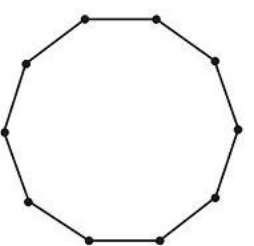    4. F-D_C974CDA5F312B769 АФДД 9654С831А0БА 534Д575ДФАФ 2402ACC59B3+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{22}\)
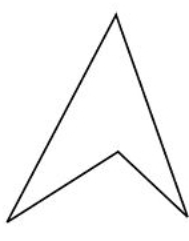    5. F-D_C61AE2278C5573ФД4129БФ11С9Ф25Е635Д76А85491ДД6020 до н.е. 92771+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{23}\)
    6. Ф-Д_АД 4БС07Е6Б 38А0СА8Ф15530Б 393Б8Ф66657905БА7Б6338ДА27АЕДА+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{24}\)
    7. Поясніть, чому наступні цифри НЕ є багатокутниками:
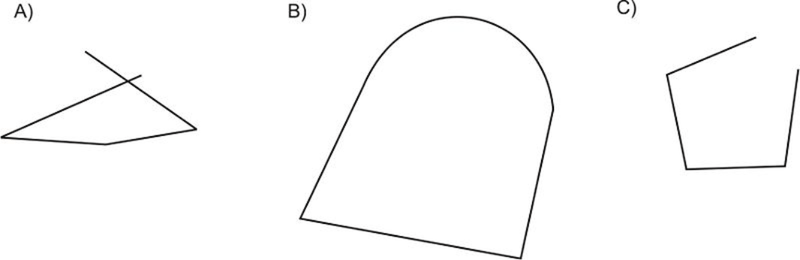      Ф-д_1 де 18 ФК 40А2А8ЕД 0ЕКА 4Е8Б90А 900301325031ФЕ0Б 141706 АЕ 806EB+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{25}\)
    8. Скільки діагоналей можна намалювати з однієї вершини п'ятикутника? Намалюйте ескіз вашої відповіді.
    9. Скільки діагоналей можна намалювати з однієї вершини восьмикутника? Намалюйте ескіз вашої відповіді.
    10. Скільки діагоналей можна намалювати з однієї вершини додекагона?
    11. Визначте кількість загальних діагоналей для восьмикутника, нонагону, декагону, ундекагону та додекагону.

    Для 12-14 визначте, чи є твердження істинним чи хибним.

    1. Багатокутник повинен бути укладений.
    2. Зірка - це опуклий багатокутник.
    3. 5-точкова зірка - декагон.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.12.

    Ресурс

    Лексика

    Термін Визначення
    діагональ (багатокутника) Небічний відрізок лінії, який з'єднує дві вершини опуклого багатокутника.
    Багатокутник Багатокутник - це проста замкнута фігура з принаймні трьома прямими сторонами.
    увігнутий Увігнутий багатокутник має принаймні один внутрішній кут більше 180 градусів. Поширеним способом ідентифікації увігнутого багатокутника є пошуки «печерної» сторони багатокутника.
    Опуклий Опуклий багатокутник не містить внутрішніх кутів більше 180 градусів.
    Діагональ Діагональ - це відрізок лінії в багатокутнику, який з'єднує непослідовні вершини.
    Зовнішні кути Зовнішній кут - це кут, утворений однією стороною багатокутника і продовженням сусідньої сторони.
    Внутрішні кути Внутрішні кути - це кути всередині фігури.
    Звичайний багатокутник Правильний багатокутник - це багатокутник з усіма сторонами однакової довжини і всіма кутами однаковою мірою.
    Вершини Вершини - це точки, де перетинаються відрізки ліній.
    Рівносторонній Багатокутник рівносторонній, якщо всі його сторони мають однакову довжину.

    Додатковий ресурс

    Інтерактивний елемент

    Відео: Сума внутрішніх кутів багатокутника

    Види діяльності: Класифікація багатокутників Питання обговорення

    Навчальні посібники: Полігони Навчальний посібник

    Практика: Класифікувати багатокутники

    Реальний світ: Полігони природи