Skip to main content
LibreTexts - Ukrayinska

6.2.5: Застосування парабол

  1. Last updated
  2. Save as PDF
  • Page ID
    55107

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Застосування парабол

    Келлі майже закінчила з главою про параболи в її математичному класі. Вона стала досить знайома із загальною формою параболи, і почала помічати використання парабол навколо неї. Одна річ, яку вона ще не зрозуміла, - це те, чому страви супутникового телебачення - це 3D-параболи. Вона впевнена, що це не збіг, але не знає, що це таке параболічна форма, яка важлива.

    Ти знаєш?

    Застосування парабол

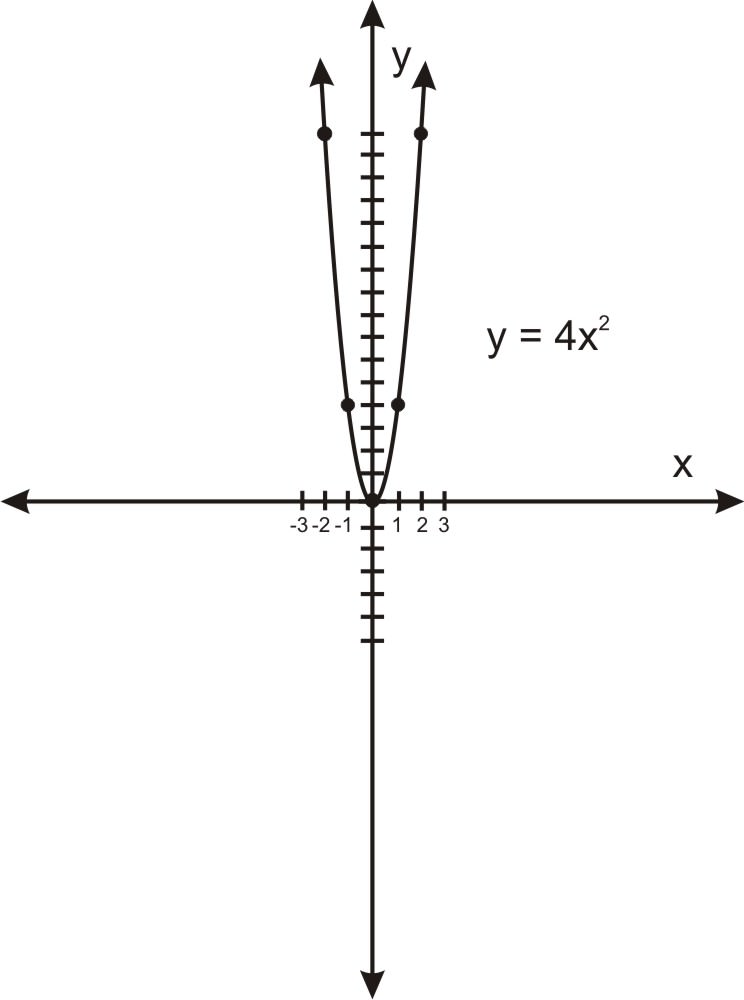
    Є дуже цікава властивість парабол. Це той факт, що всі параболи мають однакову форму. Або, кажучи мовою геометрії, будь-які дві параболи схожі один на одного. Це означає, що будь-яку параболу можна масштабувати або вивести іншу параболу точно такої ж форми. Це може зіткнутися як дивно, адже параболи, де\(\ x^{2}\) має великий коефіцієнт, безумовно, виглядають набагато «крутіше», ніж параболи з малим коефіцієнтом при розгляді в одній області, як показано на графіках нижче.

    а. високий і худий:

    Ф-Д_ФК 779Ф812Е3БФ БЦС 9Б11180Д4 А5 АБ 52ЕБ8Д7500Е821170179С7С+зображення_крихіткий+зображення_крихіткий.JPG

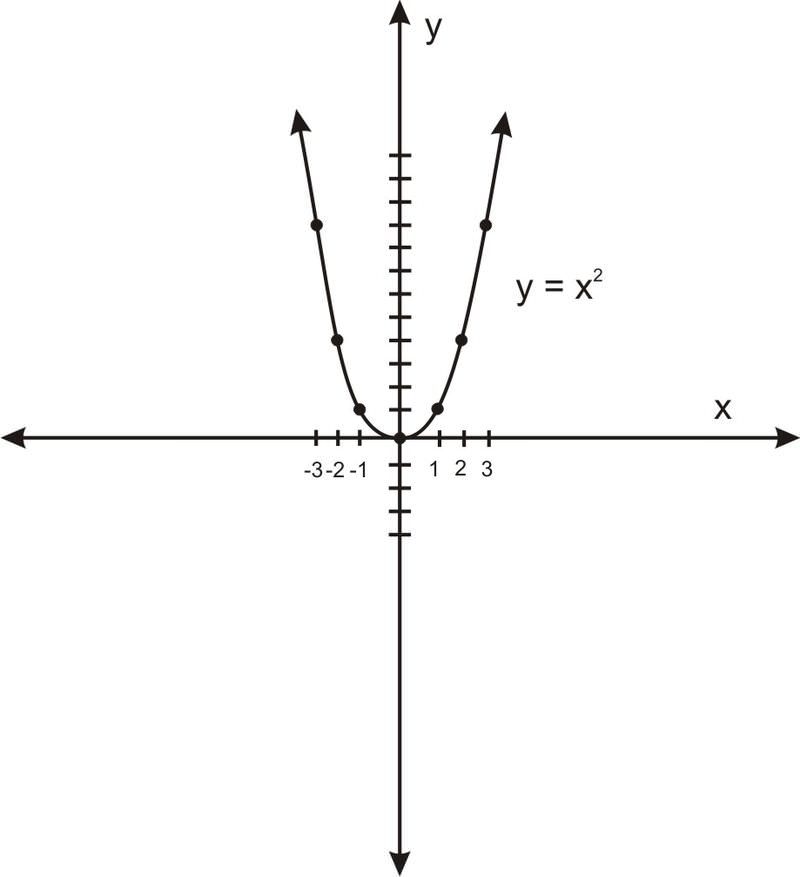
    б. короткі і широкі:

    Ф-Д_АБ59467Е5898А60А7 ААААА146858Б6447353 БЕ655Д14075КФА9С785Б+зображення_крихіткий+зображення_крихіткий.jpg

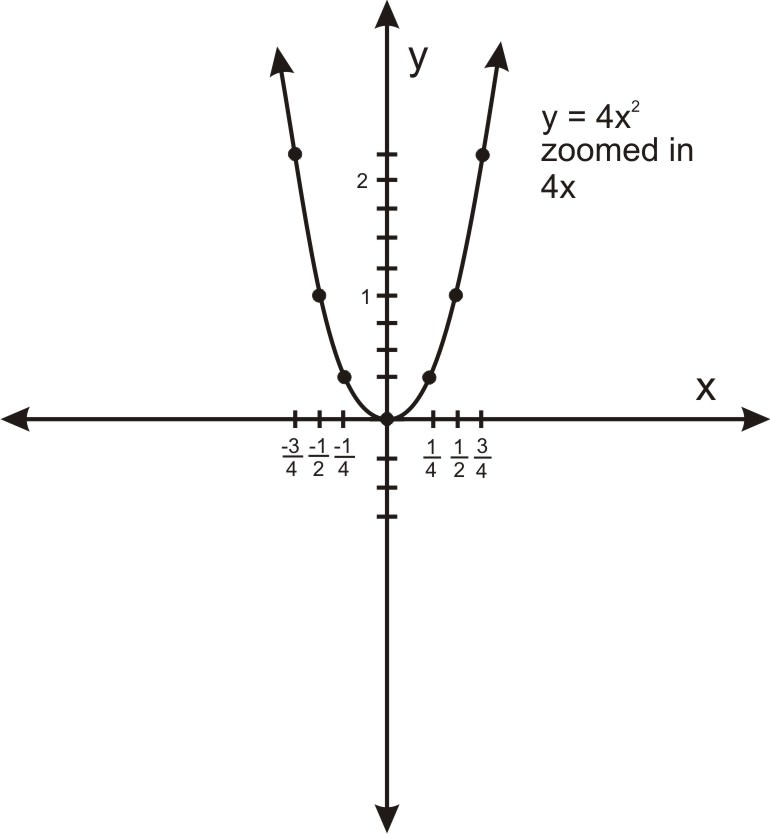
    Але коли одна з парабол масштабується відповідним чином, ці параболи ідентичні:

    а. високий і худий - збільшено в 4 рази:

    F-D_71509790464ФБА 5Б3136А 1ЕД8Ф837Е638711Ф60Д1566974 КД07883 змінного струму+зображення_крихіткий+зображення_крихіткий.jpg

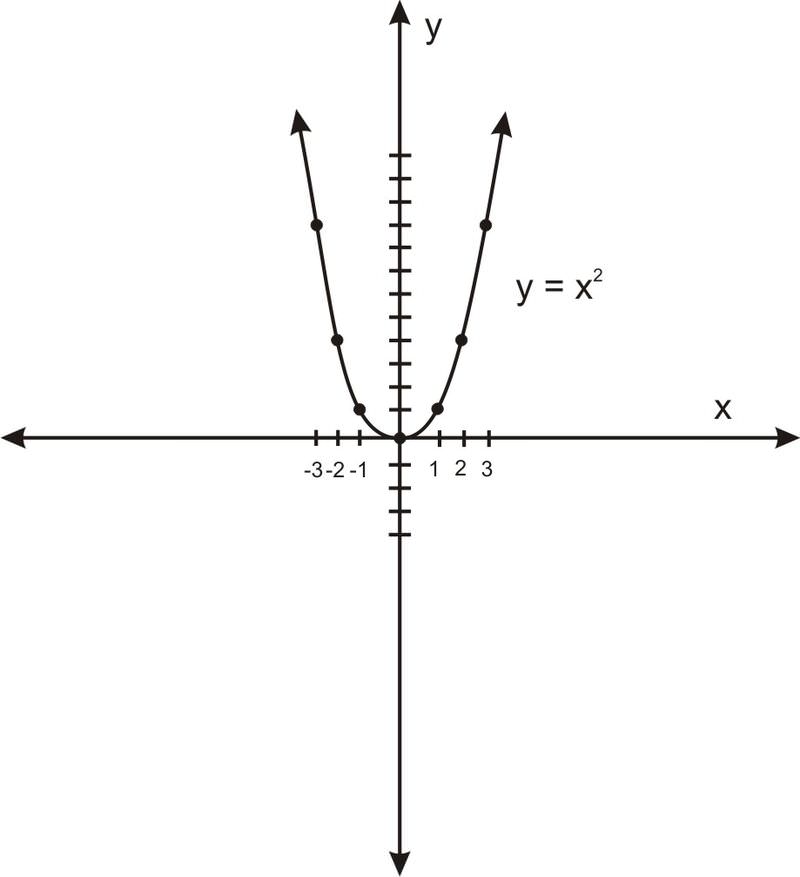
    б. короткі і широкі:

    Ф-Д_80498Ф1БФ Ф 4300Д3ФБ Б 8А17275Б1АД 4Б0ФД463Ф814С94090811Ф7ЕД6+зображення_крихіткий+зображення_крихіткий.jpg

    Цей факт про параболи можна побачити з точки зору алгебри, враховуючи той факт, що всі параболи генеруються з лінії, а точки не на цій лінії. Ця конфігурація генеруючих об'єктів, лінії та точки, завжди однакова форма. Будь-яка інша лінія і точка виглядають точно так само - просто збільшуйте або зменшуйте масштаб, поки лінія і точка не будуть однаковою відстані один від одного. Тож форми, які генерують будь-які дві такі конфігурації, також повинні бути однаковою формою.

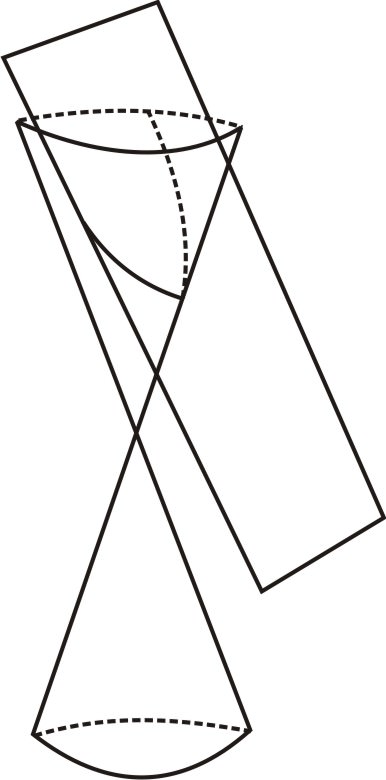
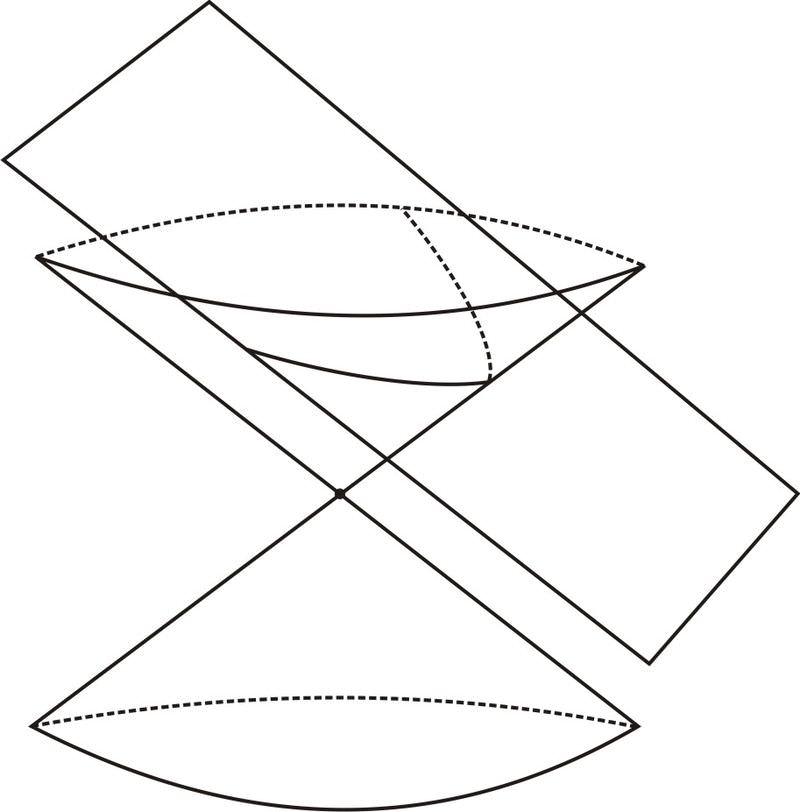
    З точки зору аналітичної геометрії, існували два фактори, які можуть вплинути на форму параболи. Перший - це відстань між січною площиною і вершиною конуса. Але конуси мають однакові пропорції в будь-якому масштабі, тому незалежно від того, яке це відстань, картинка може бути зменшена або збільшена, впливаючи на цю відстань, але не на форму конуса або площини. Таким чином, цей параметр насправді не змінює форму конічного перерізу, що призводить. Іншим фактором є форма фактичного конуса. Це його крутизна, що визначається кутом на вершині, або еквівалентно співвідношенням між радіусом і висотою в будь-якій точці. Це трохи складніше. Зовсім не очевидно, що короткі, присідаючі шишки і високі худі шишки будуть давати параболи тієї ж форми.

    а. високий і худий:

    Ф-д_А 790С5Ф229Е5Е6901А287Ф92Ф7А2 Bea3F05C463E8FA452F88 BBB7EAF+зображення_крихіткий+зображення_крихіткий.jpg

    б. короткі і широкі:

    Ф-Д_5ФДК 903Д21Б851С3Б200Е0Д2СА5Д281А68АЕ9Б049Д68БА 1Д779Ф00С+зображення_крихіткий+зображення_крихіткий.jpg

    Відповідно до того, що ми знайшли, будь-яка парабола, отримана шляхом нарізки будь-якого конуса, привела до рівняння такого вигляду:

    \(\ y=a x^{2}\)

    Ми хочемо показати, що якщо ми створимо дві такі параболи, що вони насправді мають однакову форму. Отже, припустимо, ми використовуємо дві конусні конструкції і придумаємо ці параболи:

    \(\ y=a_{1} x^{2}\)і\(\ y=a_{2} x^{2}\). Ми хочемо показати, що є якийсь масштабний коефіцієнт, називати його\(\ f\), що скорочується або збільшується\(\ y=a_{1} x^{2}\) в\(\ y=a_{2} x^{2}\). Щоб форма залишалася однаковою, коефіцієнт масштабування повинен впливати як на, так\(\ x-\) і\(\ y-\text { variables }\). Тому нам потрібно знайти\(\ f\) таке,\(\ (f y)=a_{1}(f x)^{2}\) що еквівалентно\(\ y=a_{2} x^{2}\). Перше рівняння може бути записано\(\ y=\left(a_{1} f\right) x^{2}\), що еквівалентно другому рівнянню коли\(\ a_{1} f=a_{2}\), або коли\(\ f=\frac{a_{2}}{a_{1}}\). Таке\(\ f\) завжди існує для невід'ємних чисел\(\ a_{1}\) і\(\ a_{2}\). Тож параболи дійсно мають однакову форму. Якщо\(\ a\) менше нуля, то параболу можна відбити вертикально, щоб отримати параболу такої ж форми і з позитивним коефіцієнтом\(\ a\).

    Парабола Застосування

    Палаючі дзеркала

    Діокл (240−180 до н.е.) був математиком з Стародавньої Греції, про якого ми знаємо дуже мало. Однак ми знаємо досить з кількох мізерних документів, що він думав про важливе застосування парабол. Це походить від того, що іноді називають «оптичною властивістю» парабол. Запам'ятайте оптичну властивість еліпсів: лінії з одного фокусу «відскакують» від сторони еліпса, щоб потрапити в інший фокус.

    Для парабол, оскільки параболи мають лише один фокус, директриса грає роль. Для параболи оптична властивість полягає в тому, що лінії, перпендикулярні директрисі, «відскакують» від параболи і сходяться в фокусі. Або, як варіант, лінії від фокусу «відскакують» від параболи і продовжують перпендикулярно директрисі. Як і у випадку з еліпсом, «відскакування» означає, що дві лінії відповідають параболі під рівними кутами до дотичної.

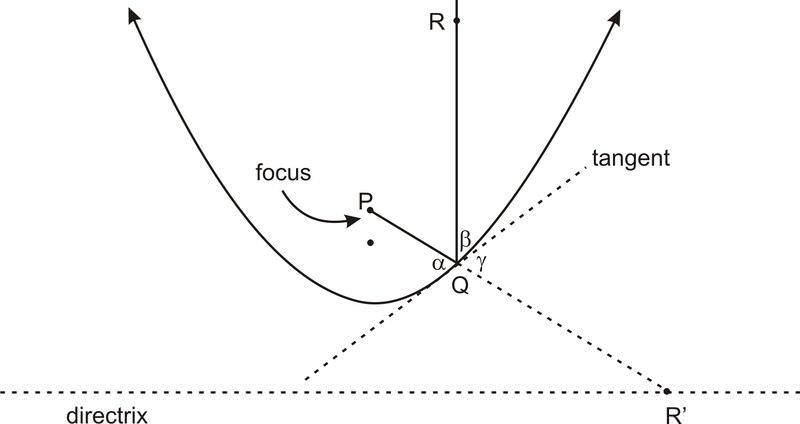
    F-D_4476454E91B6CDD3D95D9FDB858BE86594427БК 580683E72E7 февб1F+зображення_крихіткий+зображення_крихіткий.jpg

    На наведеній вище діаграмі оптична властивість стверджує, що ◻ α◻ β. Доказ схожий на доказ оптичної властивості еліпсів. На наведеній вище діаграмі P - фокус, а Q - точка на параболі. Нехай R′ буде точкою на директрисі, яка отримується шляхом розширення PQ. Тоді PR′, пряма лінія, явно найкоротша відстань між P і R′, яка проходить через дотичну лінію. Нехай R бути на лінії, що лежить прямо над Q таким чином, що QR = QR′. R можна розглядати як R′, відбивається через дотичну лінію. Потім ◻ α⟩ ◻ γ (вертикальні кути) і ◻ γ⟩ ◻ β (відбиті кути), і так ◻ α⟩ ◻ β (перехідна властивість).

    Оптична властивість має кілька цікавих застосувань. Діокл описав одне потенційне застосування в своєму документі «Про палаючих дзеркалах». Він передбачав параболічне дзеркало (в основному параболу, що обертається навколо своєї лінії симетрії), яке збирало б світло від сонця і фокусувало його на фокусній точці, створюючи достатню концентрацію світла, щоб розпочати вогонь у цій точці. Деякі стверджують, що Архімед намагався зробити таку штуковину з мідними пластинами для боротьби з римлянами в Сіракузах.

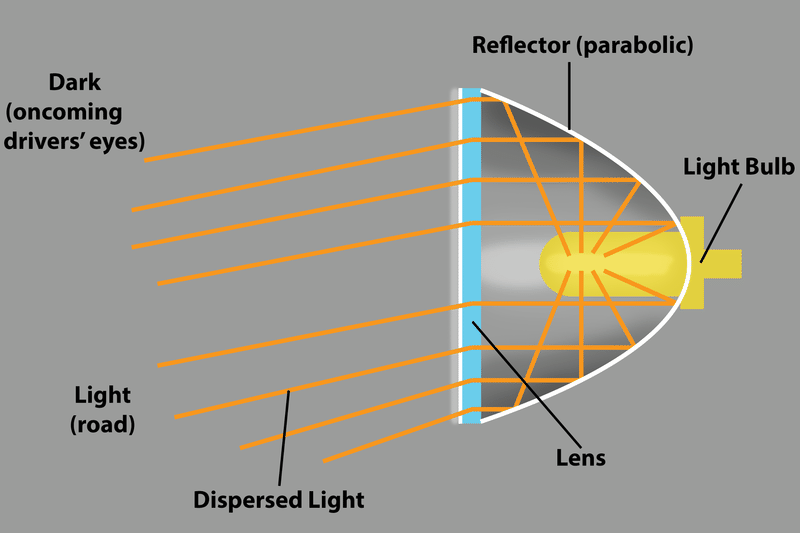
    Фари: Оптична властивість також відповідає за односпрямовані ліхтарі у формі параболи, такі як автомобільні фари. Якщо лампочка розміщена у фокусі параболічного дзеркала, світлові промені відбиваються від дзеркала паралельно один одному, утворюючи сфокусований промінь світла.

    F-д_74Б4Ф83103А18734 ЕД ДФБ77811Б26Б3ФА65051С79К3CE630046FF8C+зображення_крихіткий+зображення_крихіткий.PNG

    Телескопи Cassegrain: Супутникові телескопи використовують оптичну властивість парабол збирати якомога більше світла від далекої зірки. Антена супутника нижче має параболічну форму і відображає світло до точки посередині.

    Ф-Д_БФ 622 ЕБФ 5С06А2Д86ЕД 4АФ681СЕ5 ЕФФА9А619140Ф630163ДЕ1ДБ336+зображення_крихіткий+зображення_крихіткий.jpg

    Приклади

    Приклад 1

    Раніше вам задавали питання про те, чому супутникові телевізійні тарілки - це 3D параболи.

    Рішення

    Супутникова антена - це 3D-парабола, так що весь сигнал, який вона збирає на широкій площі, буде зосереджений у фокусі параболи, значно збільшуючи прийом.

    Приклад 2

    Поясніть, чому не всі еліпси схожі на параболи. Хоча збільшення або зменшення не працює, щоб зробити два еліпси однаковими, як ви можете змінити вигляд двох еліпсів, які мають різні форми, щоб вони виглядали однаково?

    Рішення

    Ексцентриситет еліпсів визначає форму, тому, коли ексцентриситет відрізняється для двох еліпсів, еліпси не схожі один на одного. Однак перегляд одного з еліпсів під кутом змінює сприйнятий ексцентриситет цього еліпса, і кут можна вибрати так, щоб він відповідав сприйнятому ексцентриситету ексцентриситету іншого еліпса, створюючи зображення, подібне до іншого еліпса.

    Приклад 3

    Якби нічого не використовувалося для відхилення світла, перш ніж воно увійшло в «палаюче дзеркало», де сонце повинно бути у відносині з вами та місцем, де ви хочете розпочати пожежу? Чому це обмеження? Спроектуйте спосіб обійти це обмеження.

    Рішення

    Локаль вогню повинен лежати на відрізку між вами і сонцем. Це проблема, тому що, щоб почати наземний вогонь, вам доведеться почекати до вечора, коли сонце низько в небі, щоб ви могли націлити об'єктив на землю, на жаль, сонце не так яскраво ввечері, щоб ви втратили значну кількість енергії. Об'єктив або дзеркало, що змінює кут сонячних променів, може допомогти вам обійти це обмеження.

    Приклад 4

    На наведеній вище схемі автомобільної фари об'єктив спрямовує промені світла вниз, щоб тримати їх від очей зустрічних водіїв, якщо це було єдиною метою об'єктива, в якості альтернативи об'єктив може бути опущений, а фара може бути просто трохи нахилена вниз. Але є й інше призначення об'єктива. Що це таке?

    Рішення

    Лінза також розширює масив світла, тому його називають «розсіяним світлом». Без об'єктива фара висвітлювала б лише смужку шириною самої фари, що було б не дуже корисно для водіння.

    Приклад 5

    Антена супутникової антени повинна бути побудована у формі параболоїда. Параболоїд утворюється обертанням параболи з фокусом в точці (25, 0) і директрисі\(\ x=−25\) навколо осі х, де x і y знаходяться в дюймах. Діаметр антени повинен бути 80 дюймів.

    1. Знайдіть рівняння параболи і область x.
    2. Намалюйте графік параболи, показуючи розташування фокуса.
    3. Приймач повинен бути розміщений у фокусі. Дизайнер попередив, що користувач або установник повинен подбати про те, що приймач вдариться об землю і може бути пошкоджений, якщо антена буде розміщена «обличчям вниз». Алгебраїчно визначити, чи правильно це спостереження.

    Рішення

    1. \(\ x=\frac{1}{100} y^{2}\)

      Домен - це додатне дійсне число, встановлене.

    2. Намалюйте графік параболи, показуючи розташування фокуса.

      F-D_61 ЕС609Б535Е 6С22Ф7ДА 37548984 КБ5Е6165Б3А3С870 Баб871 С44163+зображення_крихіткий+зображення_крихіткий.PNG

    3. Так, як виявлено в частині a і показано на графіку частини b, фокус знаходиться на x = 25, тоді як блюдо поширюється лише на x = 16.

    Рецензія

    1. футбол з початковою вертикальною швидкістю 96 футів в секунду. Через скільки секунд м'яч досягне максимальної висоти над рівнем моря? Яка максимальна висота?
    2. Рушниця розряджається вертикально вгору на висоті 3 фути над землею. Якщо куля має початкову дульну швидкість 200 футів в секунду, якої максимальної висоти вона досягне до того, як почне падати на землю? а) 628 фут (ів) (б) 1 878 фут (ів) (20,87 фут (д) 199.33 фут (ів)
    3. Надмірно завзятий гольфіст хіти флоп постріл з піску клин, щоб вийти з кута піску поїздки з початковою вертикальною швидкістю 45 футів в секунду. Яка максимальна висота, яку буде досягати м'яч для гольфу? а) 45 фут (ів) (б) 13.19 фут (ів) 36.64 фут (г) 95.26 фут (ів)
    4. Ви стоїте на вершині пагорба висотою 1680 футів і кидаєте невелику м'яч вгору. У кожну секунду ви вимірюєте відстань кулі від землі. Рівно t секунд після того, як ви кидаєте об'єкт, його висота, (вимірюється в футах)\(\ h(t)=-16 t^{2}+256 t+1680\) є а) Знайдіть\(\ h(3)\) положення м'яча через 3 секунди після того, як ви кидаєте його. б) Скільки подорожує об'єкт протягом двох секунд між 5 секундами і 7 секундами? в) Скільки часу потрібно, щоб об'єкт досяг висоти 2640 футів? г) Скільки часу потрібно, щоб об'єкт потрапив на землю?
    5. Студент, який бере участь у грі в удар м'яч ногою м'яч з початковою вертикальною швидкістю 32 футів в секунду. Його висота над землею в футах задається тим,\(\ s(t)=-16 t^{2}+32 t\) де t - час у секундах. Яку максимальну висоту досягає м'яч? ПІДКАЗКА - Графік параболи (вам потрібно лише потурбуватися про розділ, де 0≤t≤2 або переписати рівняння, щоб знайти вершину.
    6. Арка над входом на зачаровану стежку має параболічну форму, арка має висоту 25 футів і знаходиться між опорними стовпами 30 футів. Знайдіть рівняння, яке моделює арку, використовуючи вісь x для представлення землі парку. Створіть фокус і директрису.
    7. Супутникова антена має параболічну форму діаметром 80 метрів. Зібрані телевізійні сигнали зосереджені на одній точці, званої «фокусною» точкою, яка є фокусом параболоїда (перетин параболи). Якщо фокусна відстань дорівнює 45 метрам, знайдіть глибину тарілки, округлену до одного знака після коми.
    8. Коли заходять нові магістралі, вони часто проектуються з параболічними поверхнями, які дозволяють воді стікати. Прокладається нова магістраль, вона шириною 32 футів і на 4 футів вище в центрі шосе, то з боків. а) Знайдіть рівняння, якщо парабола, яка моделює поверхню шосе (припустимо, що походження знаходиться в центрі шосе) б) Як далеко від центру шосе знаходиться поверхня дороги .1 ноги нижче, ніж посередині?
    9. Внутрішня відстань ескізу арки - 8см, а висота арки - 9см. Припускаючи масштаб 1 см = 2m, розробте формулу, яка обчислює фактичну висоту внутрішнього краю цієї конструкції (y), в метрах на будь-якій горизонтальній відстані x, виміряної від початкової точки, яка є підлогою в центрі арки.

    Побудовано новий міст для пішохідного руху через річку. Дві вежі на обох кінцях мосту мають висоту 50 футів і 300 футів один від одного. Опорні кабелі (2) з'єднані у верхній частині веж і висять у кривій, яка утворює форму параболи. Існують вертикальні кабелі, які з'єднують доріжку з опорними кабелями. Ці кабелі підключаються кожні 15 футів від доріжки до опорних кабелів. У центрі мосту парабола знаходиться на 5 футах над доріжкою.

    Спеціальна кабельна компанія назад на схід продає кабель за $52.75 за 10 футів із вартістю доставки 300.00 доларів за все замовлення. Кабелі R US, на Західному узбережжі продає кабель за $432.90 за 100 футів з доставкою $350,00 за все замовлення. Кабель потрібно було придбати або довжиною 10 футів від SCC, або довжиною 100 футів від CRUS. Після придбання кабелі можна розрізати або зварювати між собою.

    1. Напишіть рівняння для параболи, яка представляє кожен з опорних кабелів.
    2. Визначте кількість потрібних вертикальних кабелів.
    3. Визначте довжину кожного з вертикальних тросів.
    4. Скільки коштує закупівля необхідних матеріалів у кожної компанії?

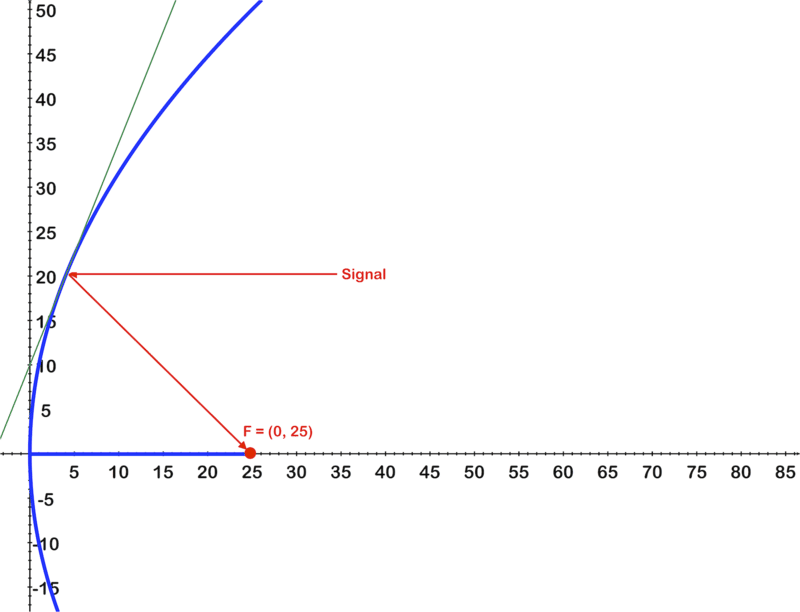
    Подивіться на зображення. Він показує параболічний переріз антени супутникової антени. Рівняння для параболи\(\ x=0.01 y^{2}\)

    F-D_61 ЕС609Б535Е 6С22Ф7ДА 37548984 КБ5Е6165Б3А3С870 Баб871 С44163+зображення_крихіткий+зображення_крихіткий.PNG

    1. У чому фокус параболи, як показано на зображенні?
    2. Радіосигнал надходить при y = 20 як позначено червоним кольором. Визначте, де промінь вражає параболу, задайте координати.
    3. Визначте вимір кута між вхідним променем та лінією між точкою удару та фокусом.
    4. Вхідний промінь і його відбитий промінь роблять кути рівної міри з лінією, дотичною до криволінійної поверхні. Використовуйте тільки що виміряний кут між сигналом і відбитою лінією, щоб обчислити міри кутів між вхідним сигналом і дотичною до точки удару і від дотичної до відбитого променя. Вони однакові? Виміряйте транспортиром, щоб підтвердити свої розрахунки.
    5. Знайдіть рівняння для дотичної прямої. Використовуйте кут C, щоб знайти його нахил.
    6. Випадковим чином вибираємо інший вхідний промінь. Обчисліть кути, як і раніше. Чи є вхідний промінь дотичним до параболи в точці, де вхідний промінь вражає графік? Звідки ти знаєш?
    7. Що ви можете сказати про напрямок відбитого променя, коли вхідний промінь паралельний осі параболи? Чи можете ви зрозуміти, чому використовується назва «фокус» і чому телевізійні супутникові антени та інші підслуховуючі пристрої виконані у формі параболоїда?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.5.

    Ресурси

    Лексика

    Термін Визначення
    палаюче дзеркало Палаюче дзеркало - це високо відбиваюча параболічна тарілка, яка використовується для фокусування сонячного світла на одній точці, фокусі параболи.
    Еліпс Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
    еліпси Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
    Парабола Парабола - це множина точок, що знаходяться на рівній відстані від фіксованої точки внутрішньої кривої, яка називається «'focus"', і лінія на зовнішній стороні, яка називається «'directrix"'. Директриса буває вертикальною або горизонтальною, в залежності від орієнтації параболи.
    параболічна тарілка Параболічна тарілка - це поверхня, породжена параболою, що обертається навколо своєї осі симетрії.
    Односпрямований Односпрямований означає фокусування в одному (uni-) певному напрямку.