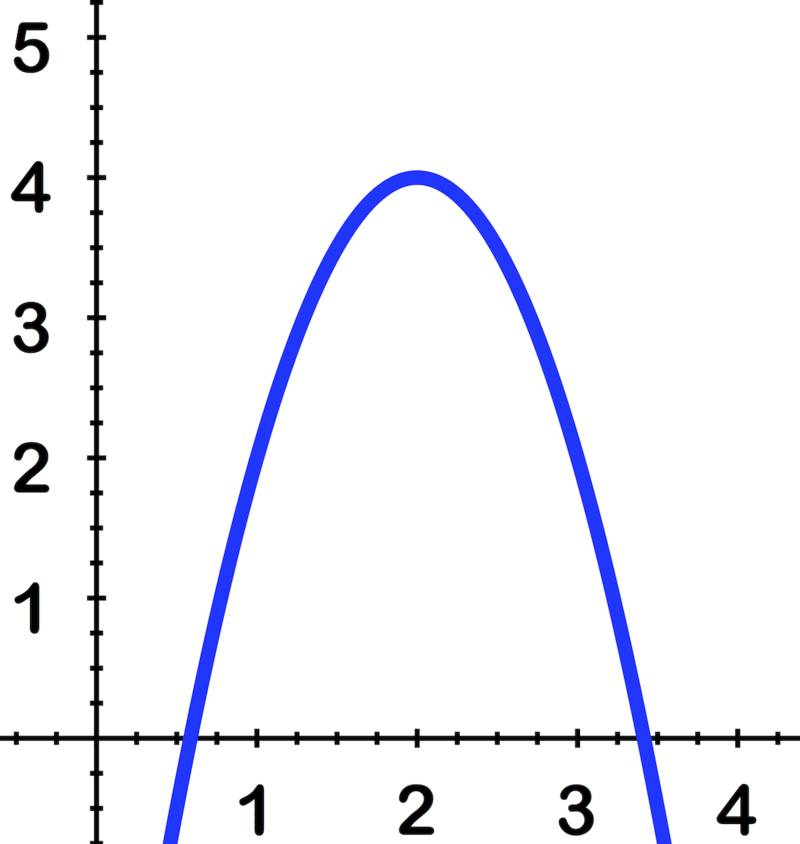
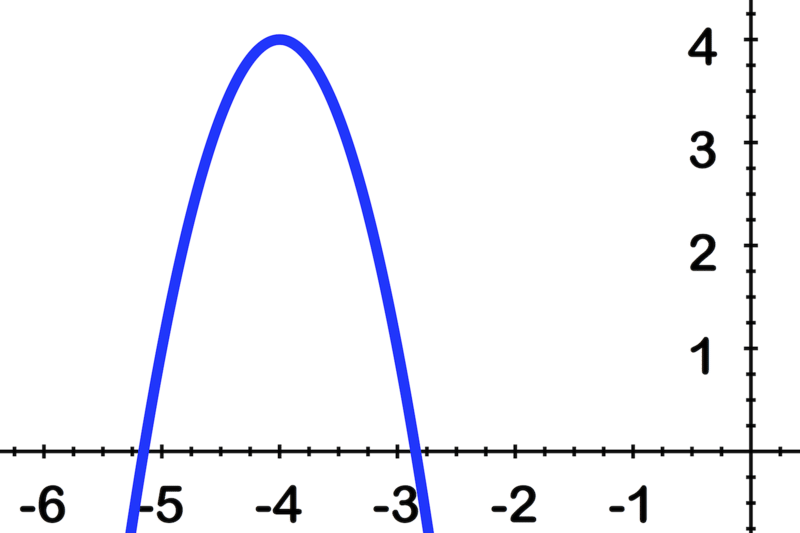
6.2.4: Параболи та аналітична геометрія
- Page ID
- 55099
Параболи та аналітична геометрія
Брендін графує параболи як частину свого домашнього завдання. Йому знайома стандартна форма параболи:\(\ y=a x^{2}\), і більш довга форма:\(\ y-k=a(x-h)^{2}\).
На своїй третій проблемі він стикається з корчем. Він значно спростив рівняння і намагається змусити його відповідати стандартній формі, але він продовжує придумувати це:\(\ x-4=3(y-3)^{2}\). Він не може зрозуміти, чому термін y є квадратом, а не термін x.
Що тут відбувається?
Параболи та аналітична геометрія
Це наш другий урок про параболи. На початковому уроці ми досліджували параболу, використовуючи формулу відстані, і торкнулися використання фокусу та директриси. На цьому уроці ми спочатку розглянемо параболи з точки зору «аналітичної геометрії», а потім працюємо кілька прикладів з фокусом і директрикою параболи.
Пошук рівняння параболи за допомогою аналітичної геометрії
Розглянемо конус, орієнтований в просторі, як на фото нижче:
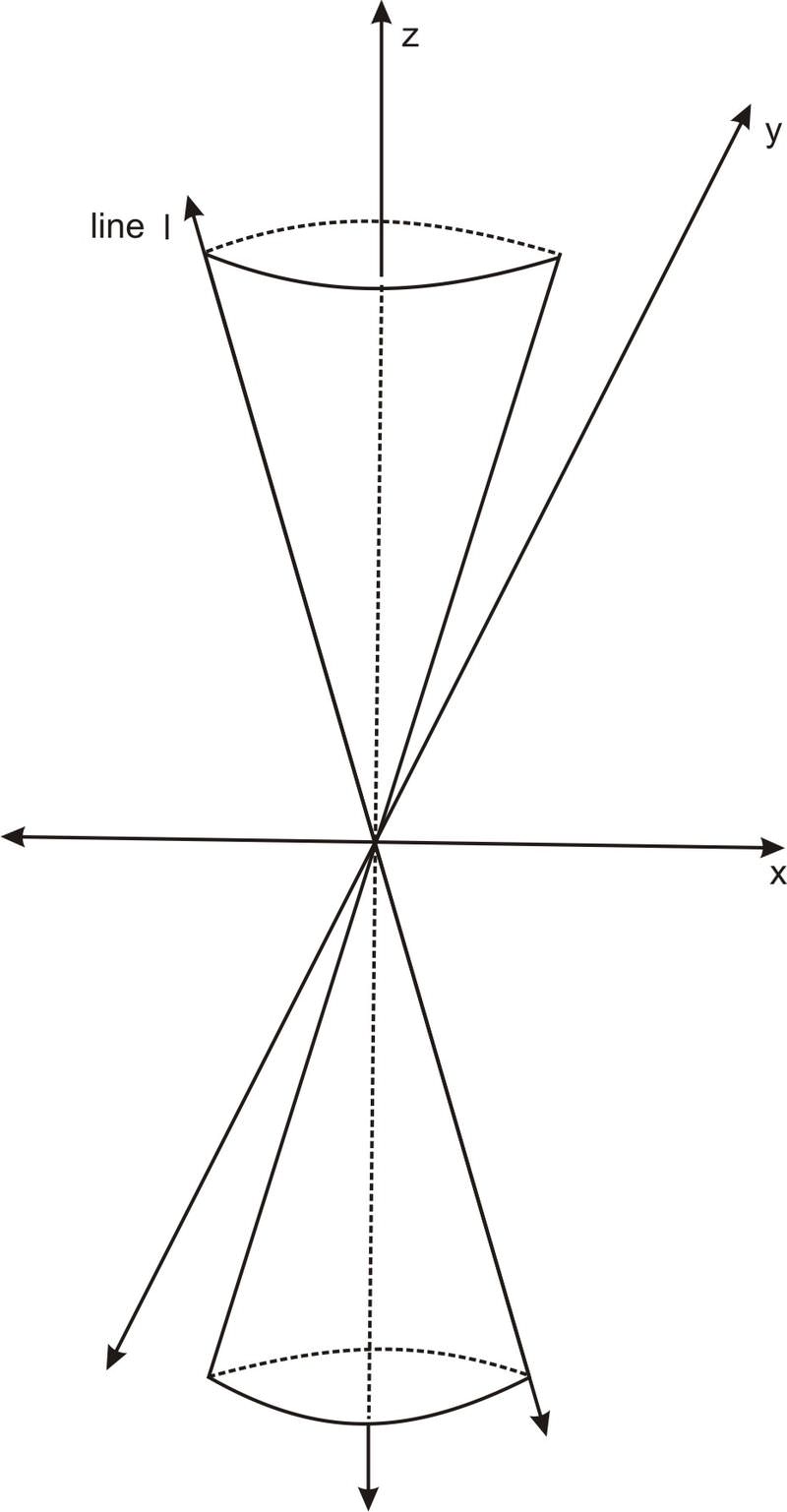
Якщо конус відкривається під таким кутом, що в будь-якій точці його радіус до висоти дорівнює a, то конус можна визначити як множину точок таким чином, щоб відстань від осі z в рази перевищувала z−координату. Або, іншими словами, множина точок (x, y, z) задовольняє:
\(\ \sqrt{(x-0)^{2}+(y-0)^{2}}=a z\)
або
\(\ x^{2}+y^{2}=a^{2} z^{2}\)
Це рівняння працює для від'ємних значень x, y та z, даючи загальне рівняння для двостороннього конуса.
Щоб розглянути перетин цього конуса з площиною, паралельною лінії,\(\ l\) зазначеної на схемі вище, найзручніше повернути весь конус навколо\(\ y\) осі, поки ліва сторона конуса не стане вертикальною, потім перетинати її з вертикальною площиною, перпендикулярною \(\ x\)−вісь. Таке обертання залишає змінну\(\ y\) −змінною. Щоб побачити, що він робить зі\(\ z\) змінними\(\ x\) і, давайте подивимося, що відбувається з точкою\(\ (x,z)\) на\(\ xz\) −площині, коли вона повертається на кут θ.
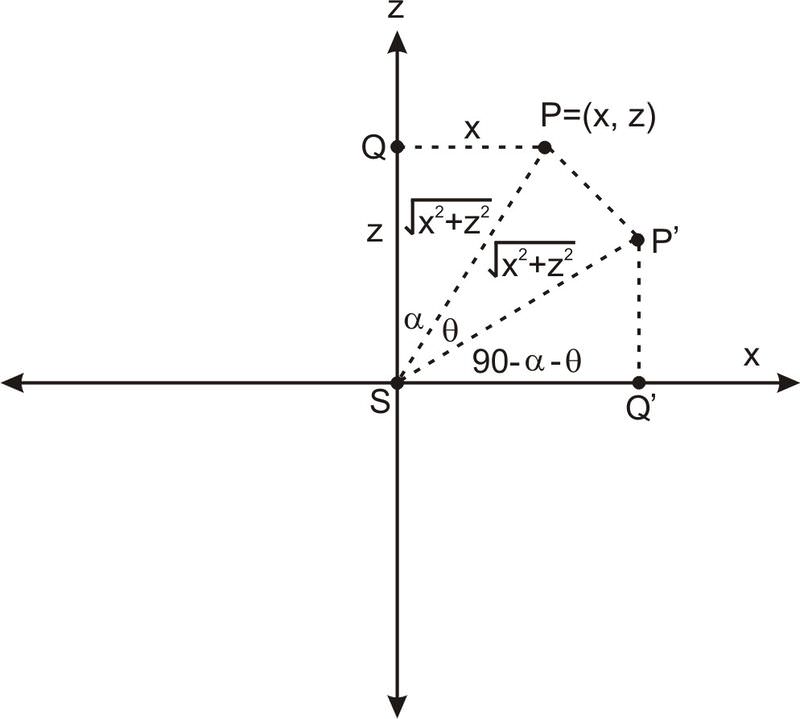
На наведеній вище схемі,\(\ P(x, z)\) повертається на кут θ до точки\(\ P^{\prime}\). Ми відзначили довжини сторін\(\ Q P=x\) і\(\ S Q=z\). За теоремою Піфагора,\(\ S P=\sqrt{x^{2}+z^{2}}\). У нас теж є\(\ S P^{\prime}=\sqrt{x^{2}+z^{2}}\), так як обертання залишає відстань від початку незмінним. Щоб знайти\(\ x\) −координати нашої повернутої точки\(\ P^{\prime}\), ми можемо використати той факт, що
\(\ \cos (90-\alpha-\theta)=\frac{S Q^{\prime}}{\sqrt{x^{2}+z^{2}}}\). Але за властивостями косинуса ми маємо:
\(\ \cos (90-\alpha-\theta)=\sin (\alpha+\theta)\),
і заміна за допомогою формули додавання синуса дає нам:
\(\ \frac{S Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\sin (\alpha) \cos (\theta)+\cos (\alpha) \sin (\theta)\),
яку ми можемо використовувати нашу діаграму, щоб змінити на:
\(\ \frac{S Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\frac{x}{\sqrt{x^{2}+z^{2}}} \cos (\theta)+\frac{z}{\sqrt{x^{2}+z^{2}}} \sin (\theta)\)
що спрощує:
\(\ S Q^{\prime}=x \cos (\theta)+z \sin (\theta)\)
Щоб знайти\(\ x\) −координати нашої повернутої точки\(\ P^{\prime}\), ми можемо використати той факт, що
\(\ \sin (90-\alpha-\theta)=\frac{P^{\prime} Q^{\prime}}{\sqrt{x^{2}+z^{2}}}\). Але за властивостями синуса ми маємо:
\(\ \sin (90-\alpha-\theta)=\cos (\alpha+\theta)\)
і заміна формулою додавання косинусів дає нам:
\(\ \frac{P^{\prime} Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\cos (\alpha) \cos (\theta)-\sin (\alpha) \sin (\theta)\),
яку ми можемо використовувати нашу діаграму, щоб змінити на:
\(\ \frac{P^{\prime} Q^{\prime}}{\sqrt{x^{2}+z^{2}}}=\frac{z}{\sqrt{x^{2}+z^{2}}} \cos (\theta)-\frac{x}{\sqrt{x^{2}+z^{2}}} \sin (\theta)\)
що спрощує:
\(\ P^{\prime} Q^{\prime}=z \cos (\theta)-x \sin (\theta)\)
Озираючись назад на картинку, це означає, що координати\(\ P^{\prime}\) є\(\ (x \cos (\theta)+z \sin (\theta), z \cos (\theta)-x \sin (\theta))\). Іншими словами, при обертанні від\(\ P\) до\(\ x\) −coordinate змінюється на\(\ P^{\prime}\),\(\ x \cos (\theta)+z \sin (\theta)\) а координата\(\ z\) − змінюється на\(\ z \cos (\theta)-x \sin (\theta)\).
Якщо це обертання відбувається з кожною точкою на конусі, ми можемо замінити\(\ x\) і\(\ x \cos (\theta)+z \sin (\theta)\)\(\ z \cos (\theta)-x \sin (\theta)\) для\(\ z\) нашого рівняння конуса, в результаті чого нове рівняння для конуса після обертання на\(\ \theta\).
\ (\\ почати {вирівняний}
(х\ cos (\ тета) +z\ sin (\ тета)) ^ {2} +y^ {2} &=a^ {2} (z\ cos (\ тета) -х\ sin (\ тета)) ^ {2}\
x^ {2}\ cos ^ {2} (\ тета) +2 х z\ cos (\ тета)\ sin\ theta) +z^ {2}\ sin ^ {2} (\ тета) +y^ {2} &=a^ {2}\ лівий (x^ {2}\ sin ^ {2} (\ тета) -2 х z\ cos (\ тета)\ гріх (\ тета) +z^ {2} \ cos ^ {2} (\ тета)\ вправо.) \\
x^ {2}\ cos ^ {2} (\ тета) +2 х z\ cos (\ тета)\ sin (\ тета) +z^ {2}\ sin ^ {2} (\ тета) +y^ {2} &=a^ {2} x^ {2}\ sin ^ {2} (\ тета) -2 a^ {2} x z\ cos (\ тета)\ sin\ тета) +a^ {2} z^ {2}\ cos (\ тета))\\
x^ {2}\ cos ^ {2} (\ тета) +2 х z\ cos (\ тета)\ sin (\ тета) +z^ {2}\ sin ^ {2} (\ тета) +y^ {2} &=a^ {2} x^ {2}\ sin ^ {2} (\ тета) -2 a^ {2} x z\ cos (\ тета)\ sin (\ тета) +a^ {2} z^ {2}\ cos (\ тета))
\ кінець {вирівняний}\)
Тепер у випадку з нахиленим конусом ми хочемо нахилити конус таким чином, щоб ліва сторона стала вертикальною. Оскільки коефіцієнт\(\ a\) визначає, наскільки нахилений конус, ми можемо бачити з трикутника нижче, що\(\ \sin (\theta)=\frac{a}{\sqrt{1+a^{2}}}\) і\(\ \cos (\theta)=\frac{1}{\sqrt{1+a^{2}}}\).
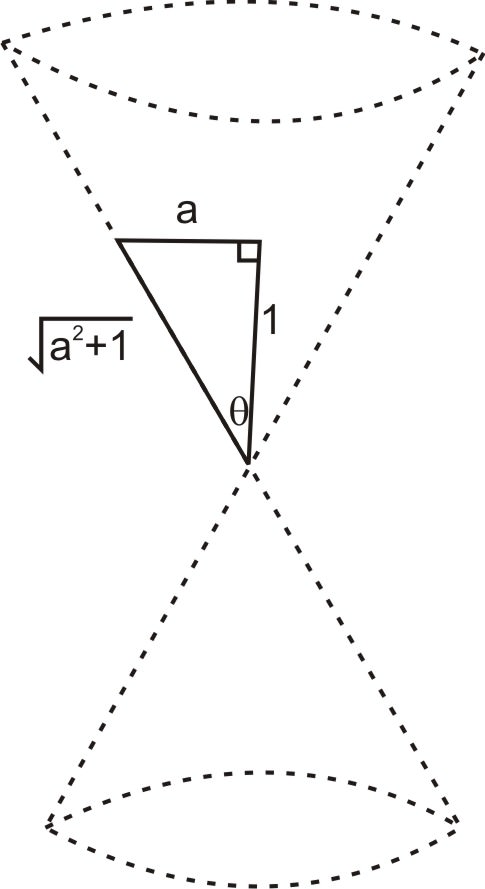
Так рівняння стає:
\ (\\ почати {вирівняний}
x^ {2}\ розриву {1} {1+a^ {2}} +2 х з\ розриву {a} {1+a^ {2}} +z^ {2}\ frac {1}} {1+a^ {2}} +y^ {2} &=a^ {2} &=a^ {2} x^ {2} ^ {2}} {1+a^ {2}} -2 a^ {2} x z\ розриву {a} {1+a^ {2}} +a^ {2} z^ {2}\ розриву {1} {1+a^ {2}}\
x^ {2} +2 х z a+z^ {2} a^ {2} +y^ {2} +y^ {2}\ ліворуч (1+a^ {2}\ праворуч) &=a^ {4} x^ {2} -2 a^ {3} x z+a^ {2} z^ {2}\\
x^ {2} +2 х z a+y^ {2}\ ліворуч (1+a^ {2}\ праворуч) &=a^ {4} x^ {2} -2 a^ {3} x z
\ кінець {вирівняний}\)
Тепер, коли ми нахилили наш конус, щоб взяти поперечний переріз, паралельний лівій стороні конуса, ми можемо просто розрізати його вертикальною площиною. Рівняння вертикальної площини, що проходить\(\ (b, 0,0)\) і перпендикулярно до\(\ x\) осі −дорівнює\(\ x=b\). Тому установка, рівна постійній в\(\ x\) рівнянні вище, дасть нам перетин нахиленого конуса і площини, паралельної одній стороні конуса. \(\ b\). Ось зображення повороту та поперечного перерізу, що лежить у\(\ xz\) −площині.
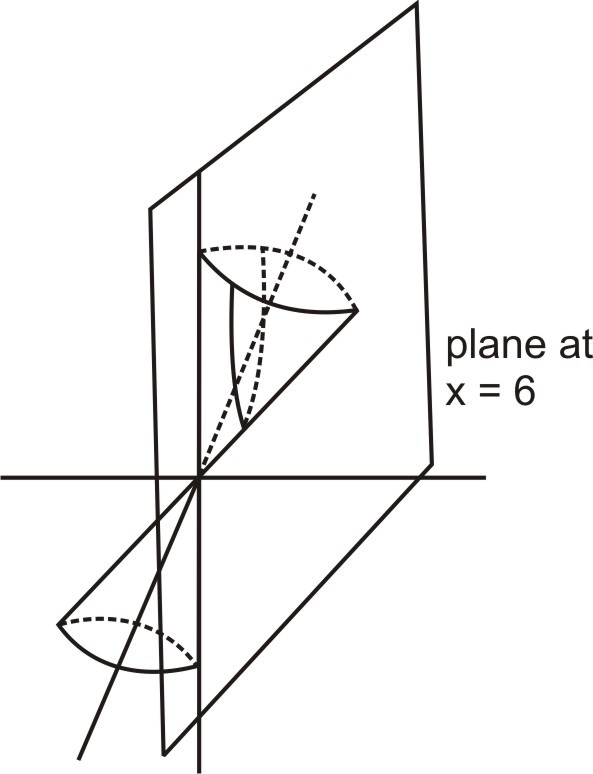
Встановлюючи\(\ x\) рівну\(\ b\) константі, маємо:
\ (\\ почати {вирівняний}
b^ {2} +2 a b z+y^ {2}\ ліворуч (1+a^ {2}\ праворуч) &=a^ {4} b^ {2} -2 a^ {3} b\\
ліворуч (2 a b+2 a^ {3} b\ праворуч) &=-y^ {2}\ ліворуч (1+a^ {2}\ ліворуч (1+a^ {2} праворуч) +a^ {4} b^ {2} -b^ {2}\\
z &=\ ліворуч (\ frac {-1-a^ {2}} {2} b+2 a^ {3} b}\ праворуч) y^ {2} +\ ліворуч (a^ {4} b^ {2} -b^ {2}\ праворуч)
\ end {вирівняний}\)
Хоча цей коефіцієнт і постійний термін здаються складними,\(\ a\) і\(\ b\) можуть бути підібрані так, щоб коефіцієнт\(\ y^{2}\) терміна міг дорівнювати будь-якому числу (цей факт ви будете досліджувати у вправі). Постійний термін можна ігнорувати, оскільки будь-яка парабола може бути зрушена вертикально на будь-яку величину.
Отже, загальна форма параболи така:
\(\ z=A y^{2}\)
де A - будь-яка константа.
Або, використовуючи більш\(\ y-\text { coordinates }\) стандартну\(\ x-\) і форму параболи є
\(\ y=a x^{2}\)
Як і раніше, це рівняння може бути адаптоване для отримання зсунутих і горизонтально орієнтованих форм.
Приклади
Раніше вам задавали питання про Брендіна, який не впевнений, чому він має\(\ y^{2}\) термін у рівнянні стандартної форми замість\(\ x^{2}\) члена.
Рішення
Брендін продовжує придумувати\(\ y^{2}\) термін, тому що це бокова парабола.
У доказі вище ми значно спростили формулу в кінці, підставивши A на
\(\ \frac{-1-a^{2}}{2 a b+2 a^{3} b}\)
Рішення
Поясніть, чому це було допустимо, показавши, що для будь-якого\(\ A\) існують константи\(\ a\) і\(\ b\) такі, що\(\ A=\frac{-1-a^{2}}{2 a b+2 a^{3} b}\)
Вирішуючи для з\(\ b\) точки зору\(\ A\) і\(\ a\), ми маємо:
\ (\\ почати {
вирівняний} A\ ліворуч (2 a b+2 a^ {3} b\ праворуч) &=-1-a^ {2}\
2 A b\ ліворуч (1+a^ {2}\ праворуч) &=-\ ліворуч (1+a^ {2}\ праворуч)\\
2 A b &= -1\\
2 A b = -1\\ 2 A b =-1\\
b\ =\ гідророзриву {1} {2 A}
\ end {вирівняний}\)
Так ми можемо встановити\(\ b=2Aa\) і відносини будуть триматися.
Намалюйте ескіз наступної параболи. Також визначте його директрису і фокус. \(\ 3 x^{2}+6 x-y=0\)
Рішення
Фактор і заповніть квадрат, щоб отримати:\(\ 3(x+1)=y+3\). Вершина знаходиться за адресою:\(\ (-1,-3)\).
Фокус -\(\ \left(-1,-2 \frac{11}{12}\right)\) Директриса - це лінія\(\ y=-3 \frac{1}{12}\)
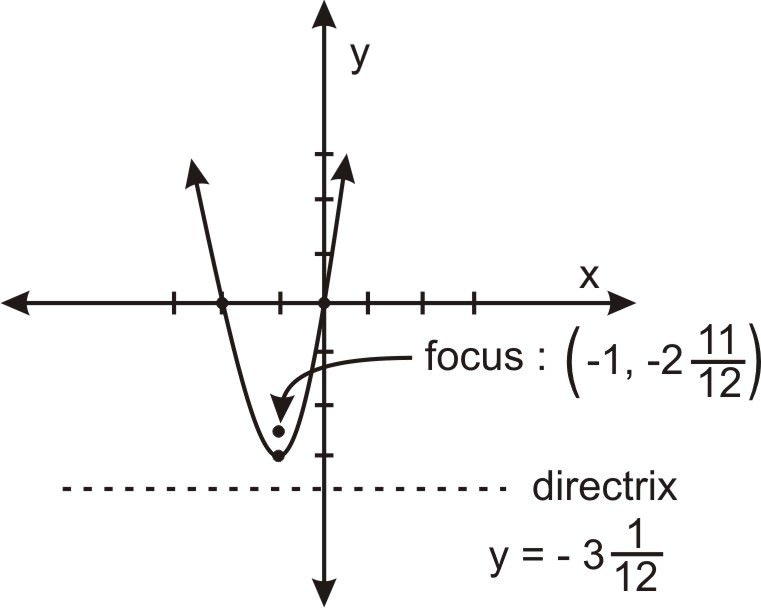
Знайдіть рівняння для параболи з директрисою\(\ y=-2\) та фокусом\(\ (3,8)\).
Рішення
Вершина знаходиться вертикально посередині між фокусом та директрисою:\(\ \frac{-2+8}{2}=3\), так само горизонтально, як фокус:\(\ x=3\) і, отже, в:\(\ (3,3)\).
Підстановка цих значень у формулу дає:
\(\ y-3=\frac{1}{20}(x-3)^{2}\)
Знайдіть рівняння для параболи з директрисою\(\ y=3\) та фокусом\(\ (2, -1)\).
Рішення
Використання вершинної форми параболи\(\ (y-k)^{2}=4 a(x-h)\):
Нагадаємо, що значення вершини y\(\ k\) є середньою точкою директриси і фокусом на прямій, перпендикулярній директрисі і перетинаючи фокус. Тому значення y вершини дорівнює 1.
Нагадаємо, що значення вершини x\(\ h\) таке ж, як і фокус, тому значення вершини x дорівнює 2
Нарешті, нагадаємо, що\(\ a\) відстань від вершини до фокуса або від вершини до директриси (які однакові):\(\ \therefore a=2\)
Заміна дає:\(\ (y-1)^{2}=8(x-2) \rightarrow y^{2}+1=8 x-16 \rightarrow y^{2}=8 x-17\)
Опишіть форму параболи, оскільки вона відноситься до конуса або подвійного конуса.
Рішення
Форма параболи, як вона відноситься до конуса або подвійного конуса, полягає в тому, що парабола представляє виявлену форму, коли порожнистий конус прорізається під кутом, рівним стороні конуса. Особливо ясно з подвійним конусом є той факт, що прорізання під більш крутим кутом призведе до двох кривих (гіпербола), а менший кут призведе до еліпса.
Намалюйте наступну параболу та визначте директрису та фокус:\(\ 4 x^{2}-3 x+y=7\).
Рішення
\(\ y=a x^{2}+b x+c\)... Згадаймо стандартну форму параболи.
\(\ a=-3|b=6| c=-2\)... Витяг a, b, c
\(\ x=\frac{-6}{2(-3)} \rightarrow x=1\)... X-координата вершини\(\ =\frac{-b}{2 a}\)
\(\ y=(-3)(1)+6(1)-2\)... Підставити обчислене значення x для розв'язання\(\ y\)
\(\ y=1\)... Вершина = (1,1)
\(\ x=1 \pm \frac{1}{\sqrt{3}}\)... Визначте Х-перехоплення за допомогою квадратичної формули
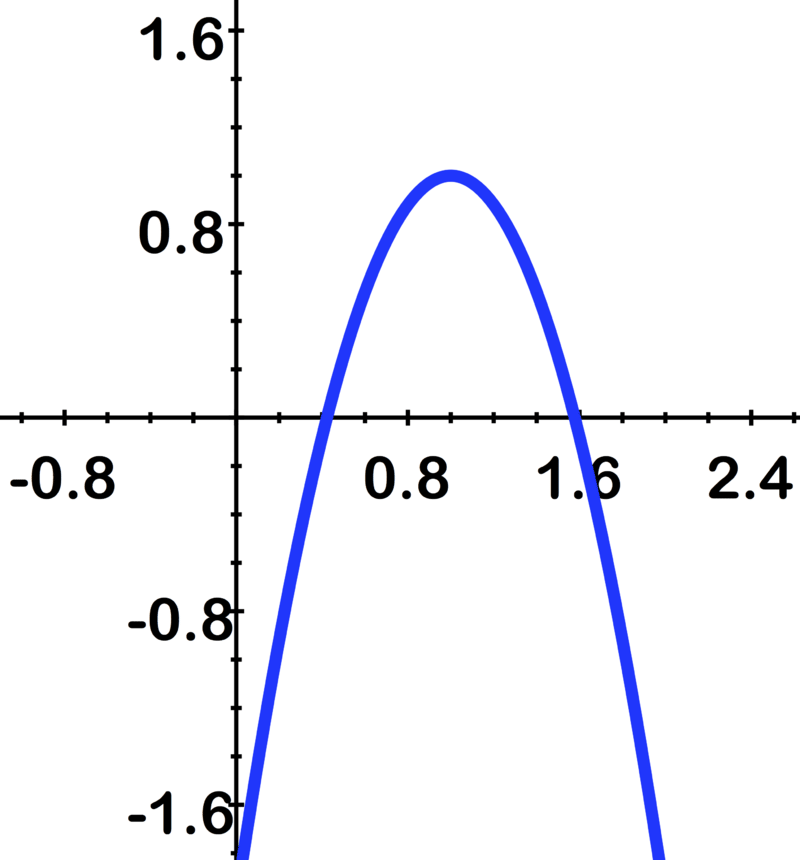
Рецензія
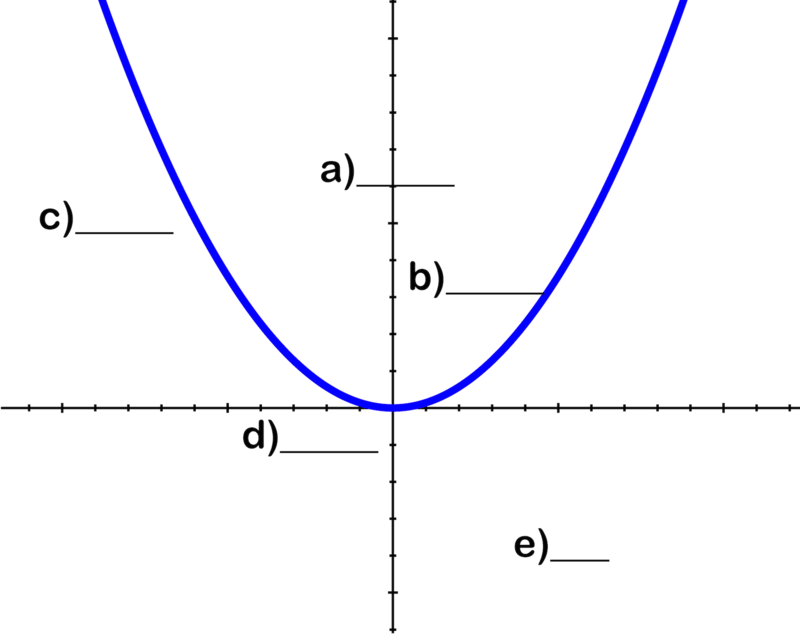
Використовуйте зображення для ідентифікації частин параболи:
- Фокус
- Вершина
- Фокусний радіус
- Директриса
- Парабола
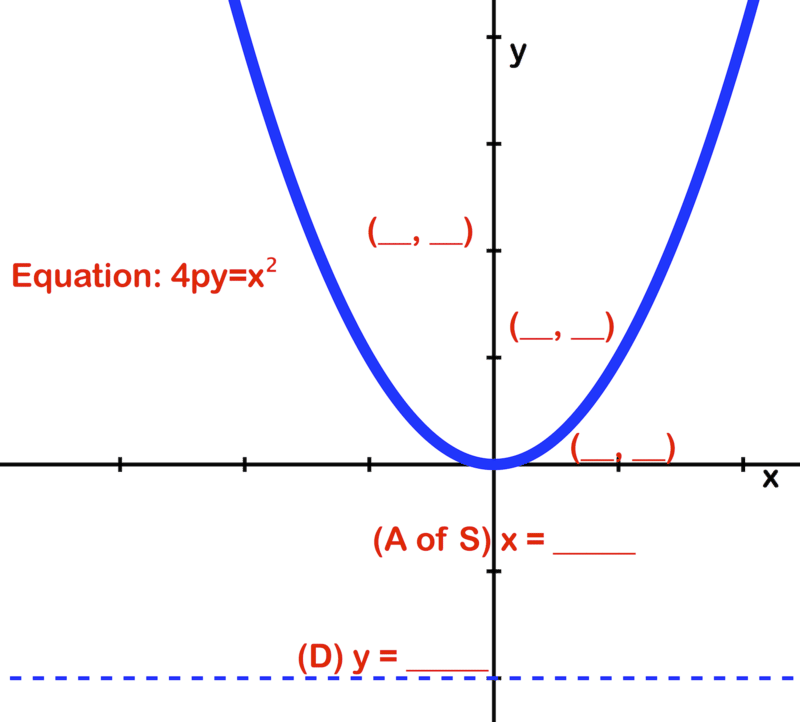
Використовуйте зображення та задане рівняння параболи, щоб визначити наступне:
- Координати фокуса
- Рівняння директриси
- Відстані фокусного радіуса
- Рівняння осі симетрії
- Координати вершини
- Знайти рівняння для параболи з директрикою: x=2 та фокусом: (0, −2)
- Знайти рівняння для параболи з вершиною: (5, −2) та директрирою: y=−5
- Знайдіть рівняння для параболи з фокусом: (3, 5) та вершиною: (3, 1)
Використовуйте зображення для ідентифікації вершини, осі симетрії та рівняння параболи:
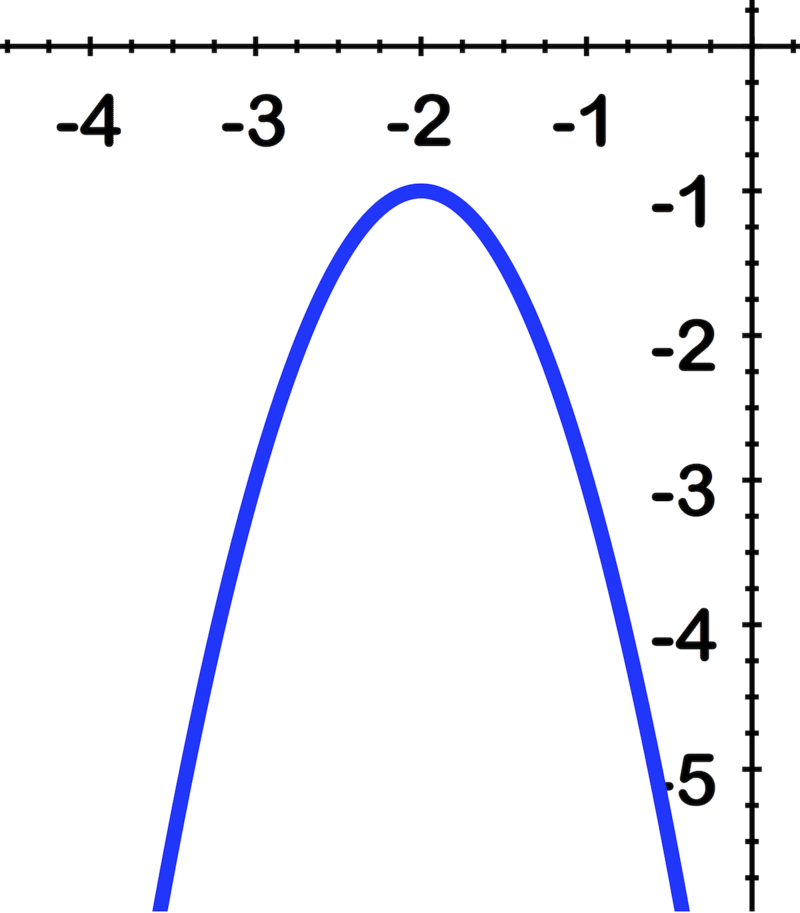
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.4.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Аналітична геометрія | Аналітична геометрія - це галузь математики, що займається моделюванням та дослідженням форм за допомогою алгебраїчних формул та системи координат. |
| вісь симетрії | Вісь симетрії параболи - це вертикальна лінія, яка проходить через вершину параболи. Парабола симетрична щодо цієї лінії. |
| Конічний | Конічні перерізи - це ті криві, які можуть бути створені перетином подвійного конуса і площини. Вони включають кола, еліпси, параболи та гіперболи. |
| директриса | Директриса параболи - це лінія, від якої парабола, здається, крива. Всі точки на параболі рівновіддалені від вогнища параболи і директриси параболи. |
| фокус | У центрі уваги параболи є точка, яка «закріплює» параболу. Будь-яка точка на параболі знаходиться точно на такій же відстані від фокуса, як і від директриси. |
| Парабола | Парабола - це множина точок, що знаходяться на рівній відстані від фіксованої точки внутрішньої кривої, яка називається «'focus"', і лінія на зовнішній стороні, яка називається «'directrix"'. Директриса буває вертикальною або горизонтальною, в залежності від орієнтації параболи. |