Skip to main content
LibreTexts - Ukrayinska

6.2.3: Параболи з будь-якою вершиною

  1. Last updated
  2. Save as PDF
  • Page ID
    55115

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Параболи з вершиною at (h, k)

    Ваше домашнє завдання полягає в тому, щоб знайти фокус параболи\(\ (x+4)^{2}=-12(y-5)\). Ви кажете, що фокус є (−4, 5). Бану каже, що фокус є (0, −3). Карлос каже, що фокус є (−4, 2). Хто з вас правильний?

    Параболи з вершиною at (h, k)

    Ви вже дізналися, що параболи не завжди мають свою вершину (0, 0). У цій концепції ми розглянемо параболи, де знаходиться вершина (h, k), навчимося знаходити фокус, директрису та граф.

    Нагадаємо, що рівняння параболи є\(\ x^{2}=4 p y\) або,\(\ y^{2}=4 p x\) а вершина - на початку. Також нагадаємо, що вершинна форма параболи є\(\ y=a(x-h)^{2}+k\). Поєднуючи два, ми можемо знайти форму вершини для коніків.

    \ (\\ почати {вирівняний}
    y &= a (x-h) ^ {2} +k\ текст {і} x^ {2} =4 р у &\ текст {Вирішити перший для} (х-ч) ^ {2}\ (x-h) ^ {2} &=\ frac {1} {a}
    (y-k) &\ text {Ми виявили, що} 4 p=\ frac {1} {a} (y-k) &\ text {Ми виявили, що} 4 p=\ frac {1} {a}\\
    (x-h) ^ {2} &=4 р (y-k) &
    \ кінець { вирівняні}\)

    Якщо парабола горизонтальна, то рівняння буде\(\ (y-k)^{2}=4 p(x-h)\). Зверніть увагу, що, незважаючи на те, що орієнтація змінена,\(\ k\) значення\(\ h\)\(\ x\) і залишаються зі\(\ y\) значеннями і відповідно.

    Знайти фокус і директрису трохи складніше. Використовуйте розширену таблицю нижче, щоб допомогти вам знайти ці значення.

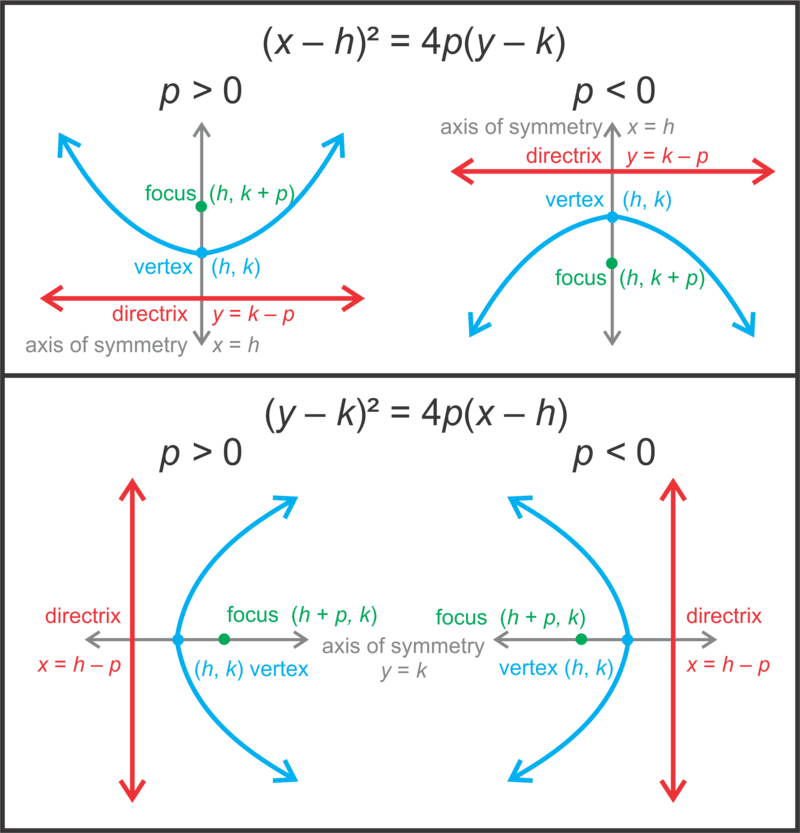
    F-D_B315 змінного струму 833D98D7C2644Ф157АЦ584КА4C02211B3F6CC51E7551D0+зображення_крихіткий+зображення_крихіткий.PNG

    Зверніть увагу, що спосіб, яким ми знаходимо фокус та директрису, не змінюється, чи\(\ p\) є позитивним чи негативним.

    Розберемо рівняння\(\ (y-1)^{2}=8(x+3)\). Ми знайдемо вершину, вісь симетрії, фокус і директрису. Потім ми визначимо, якщо функція відкривається вгору, вниз, вліво або вправо.

    По-перше, тому що\(\ y\) знаходиться в квадраті, ми знаємо, що парабола відкриється вліво або вправо. Можна зробити висновок, що парабола відкриється праворуч, оскільки 8 є позитивним,\(\ p\) тобто позитивним. Далі знайдіть вершину. Використовуючи загальне рівняння\(\ (y-k)^{2}=4 p(x-h)\), вершина дорівнює (−3, 1), а вісь симетрії -\(\ y=1\). Встановлюючи\(\ 4 p=8\), у нас є що\(\ p=2\). Додавши\(\ p\) до\(\ x\) -значення вершини, отримуємо фокус, (−1, 1). Віднімаючи\(\ p\) з\(\ x\) -значення вершини, отримаємо директрису,\(\ x=−5\).

    Давайте пографуємо параболу з наведеної вище задачі. Побудуйте вершину, вісь симетрії, фокус та директрису.

    Спочатку побудуйте всі критичні значення, які ми знайшли раніше. Потім визначте набір симетричних точок, які знаходяться на параболі, щоб переконатися, що ваша крива правильна. Якщо\(\ x=5\),\(\ y\) то або -7, або 9. Це означає, що точки (5, −7) та (5, 9) знаходяться на параболі.

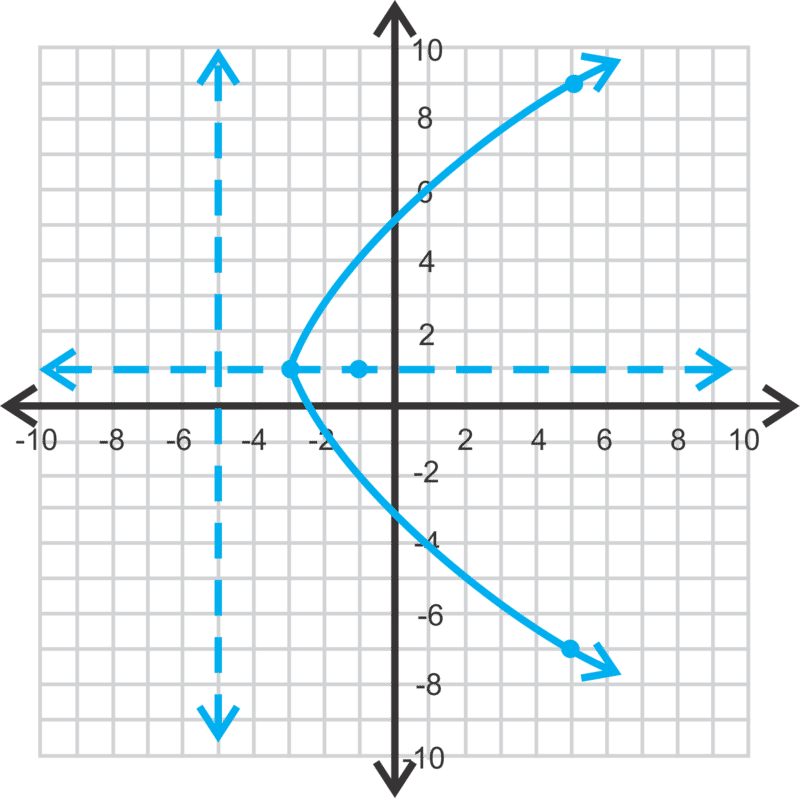
    F-D_9БК 3269 ЕАБ 39Е875Б0Б 0БА 0БА АБ 9925Е940 БА Кафе 447ФЦ757C35D0FC3+зображення_крихіткий+зображення_крихіткий.PNG

    Важливо відзначити, що параболи з горизонтальною орієнтацією не є функціями, оскільки вони не проходять тест вертикальної лінії.

    Вершина параболи дорівнює (−2, 4), а директриса - y=7. Знайдемо рівняння параболи.

    Для початку визначимося з орієнтацією цієї параболи. Оскільки директриса горизонтальна, ми знаємо, що парабола відкриється вгору або вниз (див. таблицю/малюнки вище). Ми також знаємо, що директриса знаходиться над вершиною, що робить параболу відкритою вниз і\(\ p\) буде від'ємною (якщо ви не впевнені).

    Щоб знайти\(\ p\), ми можемо використовувати вершину\(\ (h,k)\) і рівняння для горизонтальної директриси,\(\ y=k−p\).

    \ (\\ begin {вирівняний}
    7 &=4-p\\
    3 &=-p\ quad\ quad\ quad\ text {Запам'ятайте,} p\ text {є негативним через низхідну орієнтацію параболи.} \\
    -3 &=p
    \ кінець {вирівняний}\)

    Тепер, використовуючи загальну форму\(\ (x-h)^{2}=4 p(y-k)\), ми можемо знайти рівняння цієї параболи.

    \ (\\ почати {вирівняний}
    (х- (-2)) ^ {2} &= 4 (-3) (y-4)\\
    (x+2) ^ {2} &=-12 (y-4)
    \ кінець {вирівняний}\)

    Приклади

    Приклад 1

    Раніше вас попросили визначити, який учень правильний.

    Рішення

    Ця парабола має форму\(\ (x-h)^{2}=4 p(y-k)\). З таблиці, наведеної раніше в цьому уроці, ми бачимо, що в центрі уваги параболи цієї форми\(\ (h, k+p)\). Так що тепер ми повинні знайти ч, К, і р.

    Якщо\(\ (x+4)^{2}=-12(y-5)\) порівнювати з\(\ (x-h)^{2}=4 p(y-k)\), ми бачимо, що:

    1. \(\ 4=-h \text { or } h=-4\)
    2. \(\ -12=4 p \text { or } p=-3\)
    3. \(\ 5=k\)

    З цих фактів ми можемо знайти\(\ k+p=5+(-3)=2\).

    Тому фокус параболи -\(\ (−4,2)\) і Карлос правильний.

    Приклад 2

    Знайдіть вершину, фокус, вісь симетрії та директрису\(\ (x+5)^{2}=2(y+2)\).

    Рішення

    Вершина є,\(\ (-5,-2)\) і парабола відкривається, тому що\(\ p\) позитивна і\(\ x\) знаходиться в квадраті.

    \(\ 4 p=2\), Виготовлення\(\ p=\frac{1}{2}\). Фокус -\(\ (-5,-2+2)\) або\(\ (-5,0)\), вісь симетрії є\(\ x=-5\), а директриса -\(\ y=-2-\frac{1}{2}\) або\(\ y=-2 \frac{1}{2}\).

    Приклад 3

    Графік параболи з прикладу 2.

    Рішення

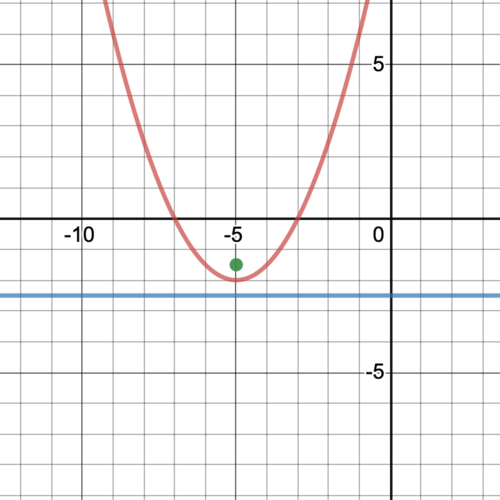
    F-D_86C9ec8FD6A83CF8BE727A86a5B7528B091C56AB523b48B8D9F2998B+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png

    Приклад 4

    Знайдіть рівняння параболи з вершиною (−5, −1) та фокусом (−8, −1).

    Рішення

    Вершина дорівнює (−5, −1), отже\(\ h=−5\) і\(\ k=−1\). Фокус має значення (−8, −1), що означає, що парабола буде горизонтальною. Ми знаємо це тому, що значення y вершини та фокусу обидва -1. Тому\(\ p\) додається або віднімається до\(\ h\).

    \(\ (h+p, k) \rightarrow(-8,-1)\)ми можемо зробити висновок, що\(\ h+p=-8 \rightarrow-5+p=-8\) і\(\ p=-3\)

    Тому рівняння\(\ (y-(-1))^{2}=4(-3)(x-(-5)) \rightarrow(y+1)^{2}=-12(x+5)\)

    Рецензія

    Знайдіть вершину, фокус, вісь симетрії та директрису парабол нижче.

    1. \(\ (x+1)^{2}=-3(y-6)\)
    2. \(\ (x-3)^{2}=y-7\)
    3. \(\ (y+2)^{2}=8(x+1)\)
    4. \(\ y^{2}=-10(x-3)\)
    5. \(\ (x+6)^{2}=4(y+8)\)
    6. \(\ (y-5)^{2}=-\frac{1}{2} x\)
    7. Графік параболи з #1.
    8. Графік параболи з #2.
    9. Графік параболи з #4.
    10. Графік параболи з #5.

    Знайдіть рівняння параболи з заданою вершиною і фокус або директриса.

    1. вершина: (2, −1), фокус: (2, −4)
    2. вершина: (−3, 6), директриса: x = 2
    3. вершина: (6, 10), директриса: y = 9,5
    4. Фокус виклику: (−1, −2), директриса: x = 3
    5. Розширення Перепишіть рівняння параболи, x 2 − 8x + 2y + 22 = 0, в стандартному вигляді заповнивши квадрат. Потім знайдіть вершину.

    Відповіді на проблеми з оглядом

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.2.

    Лексика

    Термін Визначення
    Вершинна форма Вершинна форма параболи є\(\ (x-h)^{2}=4 p(y-k)\) або\(\ (y-k)^{2}=4 p(x-h)\) де\(\ (h,k)\) знаходиться вершина.

    Атрибуції зображень

    1. [Малюнок 1]
      Кредит: Холлі Фішер
      Джерело: https://commons.wikimedia.org/wiki/File:Three_Main_Layers_of_the_Eye.png