6.2.2: Параболи та формула відстані
- Page ID
- 55106
Параболи та формула відстані
У попередніх уроках з конічних перерізів ми обговорювали як коло, так і еліпс, кожен з яких є результатом «нарізки» конуса, проясненого зліва направо. У цьому уроці ми обговоримо форму, утворену, коли ми прорізаємо лише одну сторону конуса, створюючи фігуру у формі чаші під назвою парабола.
Розглянемо фігуру «пісочний годинник», яку ми використовували в визначеннях кола і еліпса, створеного шляхом з'єднання двох нескінченних конусів на їх кінчиках. Яке обмеження було б на кут зрізу, який ми б виймали з одного з конусів, якби ми хотіли отримати лише параболу (не отримати еліпс, і ніяк не вдарити по іншому конусу)?
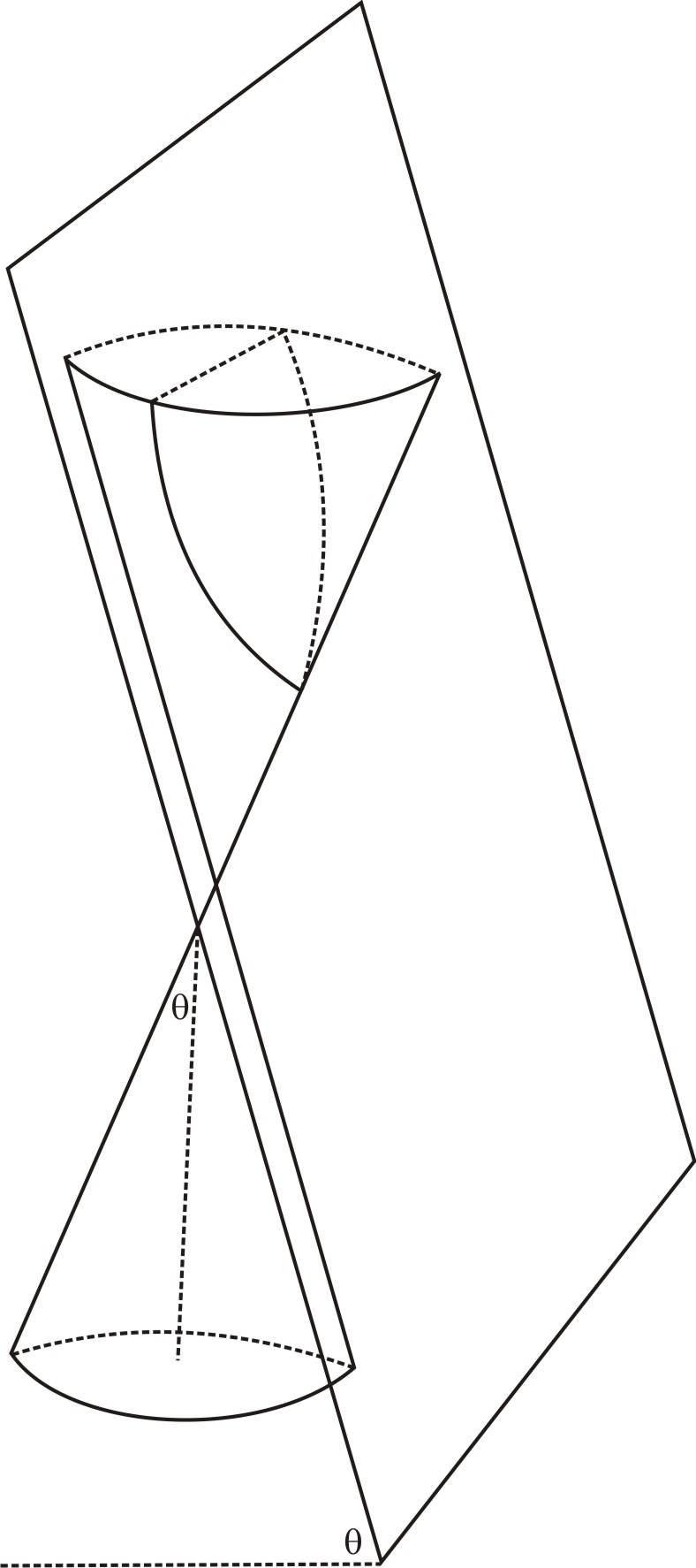
Параболи та формула відстані
Ми розглянули еліпси та кола, два випадки, коли площина перетинає лише одну сторону конуса і створює кінцевий поперечний переріз. Чи можна площині перетинати тільки одну сторону конуса, але створити нескінченний перетин?
Виходить, що це можливо тоді і тільки в тому випадку, якщо площина паралельна одній з ліній, що складають конус. Або, іншими словами, кут між площиною і горизонтом, дорівнює куту, утвореному стороною конуса і горизонтальною площиною.

На зображенні вище, якщо ви нахилите площину трохи вліво, вона відрізає кінцевий еліпс (можливо, дуже великий, якщо ви лише трохи нахилите його). Нахиліть площину вправо і вона буде перетинатися з обох сторін конуса, зробивши двосекційний конічний перетин, званий гіперболою, про який і піде мова в наступному розділі.
Коли площина паралельна з боку конуса, нескінченна форма, яка виникає в результаті перетину площини і конуса, називається параболою. Як і еліпс, він має ряд цікавих геометричних властивостей.
Рівняння параболи простіше, ніж у еліпса. Існує кілька методів виведення рівняння параболи, в цьому уроці ми досліджуємо формулу відстані.
Цей перший спосіб виникає безпосередньо з focus - властивості directrix, розглянутого в попередньому розділі. Припустимо, у нас є лінія і точка не на цій лінії в площині, і ми хочемо знайти рівняння множини точок в площині, яка є рівновіддаленою до цих двох об'єктів. Не втрачаючи жодної спільності, ми можемо зорієнтувати лінію горизонтально і точку на осі y, з початком між ними на півдорозі. Оскільки парабола - це множина точок, рівновіддалених від лінії і точки, парабола проходить через початок, (0, 0). На малюнку нижче показана така конфігурація. Точка безпосередньо між директрисою і вогнищем (початок в даному випадку) називається вершиною параболи. Припустимо, фокус розташований за адресою (0, b). Тоді директриса має бути y=−b.
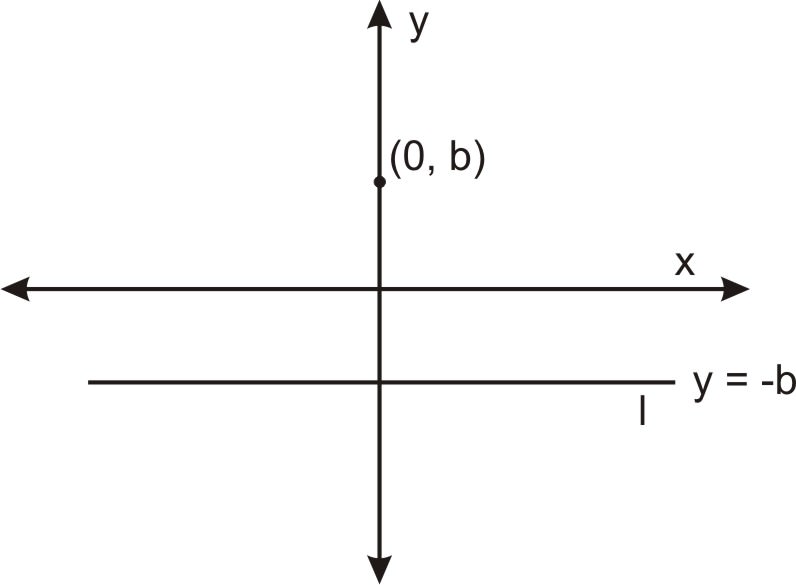
Таким чином, парабола - це сукупність точок,\(\ (x, y)\) рівновіддалених від лінії\(\ y=-b\) і точки фокусування\(\ (0, b)\). Відстань до лінії - це вертикальний відрізок від\(\ (x, y)\) вниз до\(\ (0,-b)\), який має довжину\(\ y-(-b)=y+b\). Відстань від\(\ (x, y)\) до фокусу\(\ (0, b)\) -\(\ \text { distance }=\sqrt{(x-0)^{2}+(y-b)^{2}}\) за формулою відстані. Таким чином, рівняння параболи - це множина точок, де ці дві відстані рівні.
\(\ y+b=\sqrt{(x-0)^{2}+(y-b)^{2}}\)
Оскільки відстані завжди позитивні, ми можемо квадратувати обидві сторони, не втрачаючи жодної інформації, отримуючи наступне.
\ (\\ почати {вирівняний}
y^ {2} +2 b y+b^ {2} &=x^ {2} +y^ {2} -2 b y+b^ {2}\ 2 b y &= x^ {
2} -2 б у\\ 4 b y &= x^ {2}\ y &=\ frac {1} {
4 b} x^ {2} {2}\
y &=\ розрив {1} {4 b} x^ {2}
\ кінець вирівняні}\)
Але\(\ b\) був обраний довільно і міг бути будь-яке додатне число, і для будь-якого додатного числа\(\ a\), завжди існує число\(\ b\) таке\(\ a=\frac{1}{4 b}\), що, так що ми можемо переписати це рівняння як:
\(\ y=a x^{2}\)
де\(\ a\) будь-яка константа.
Це загальна форма параболи з горизонтальною направленою, з осередком, що лежить над нею, і з вершиною біля початку. Якщо\(\ a\) негативний, парабола відбивається навколо\(\ x\) осі −, в результаті чого утворюється парабола з горизонтальною директрисою, з фокусом, що лежить під ним, і з вершиною біля початку. Рівняння може бути зрушено горизонтально або вертикально шляхом переміщення вершини, в результаті чого утворюється загальна форма параболи з горизонтальною директрисою і проходить через вершину\(\ (h,k)\):
\(\ y-k=a(x-h)^{2}\)
Перемикання\(\ x\) і\(\ y\), рівняння для параболи з вертикальною директрисою і з\(\ (h,k)\) вершиною в:
\(\ x-h=a(y-k)^{2}\)
Приклади
Раніше вам задавали питання про обмеження кута зрізу, вийнятого з однієї з конусів, якщо ви хочете тільки параболу.
Рішення
Для того, щоб отримати тільки перетин параболи, зріз повинен бути прийнятий під тим же кутом, що і сторона конуса, таким чином край зрізу проходить паралельно краю конуса і ніколи не перетинає його ні вгорі, ні внизу.
У цьому можна переконатися при уважному погляді на зображення зверху:

Намалюйте графік параболи\(\ y=3 x^{2}+12 x+17\).
Рішення
Для початку нам потрібно перерахувати коефіцієнт\(\ x^{2}\) терміна і завершити квадрат:
\ (\\ почати {масив} {l}
y=3\ ліворуч (x^ {2} +4 х\ праворуч) +17\\
y=3\ вліво (x^ {2} +4 x+4\ праворуч) +17-12\
y=3 (x+2) ^ {2} +5
\ end {масив}\)
Тепер пишемо його у вигляді\(\ y-k=a(x-h)^{2}\):
\(\ y-5=3(x+2)^{2}\)
Отже, вершина знаходиться за адресою (−2, 5), і будуючи декілька значень x по обидва боки від x = −2, ми можемо намалювати наступний ескіз параболи:
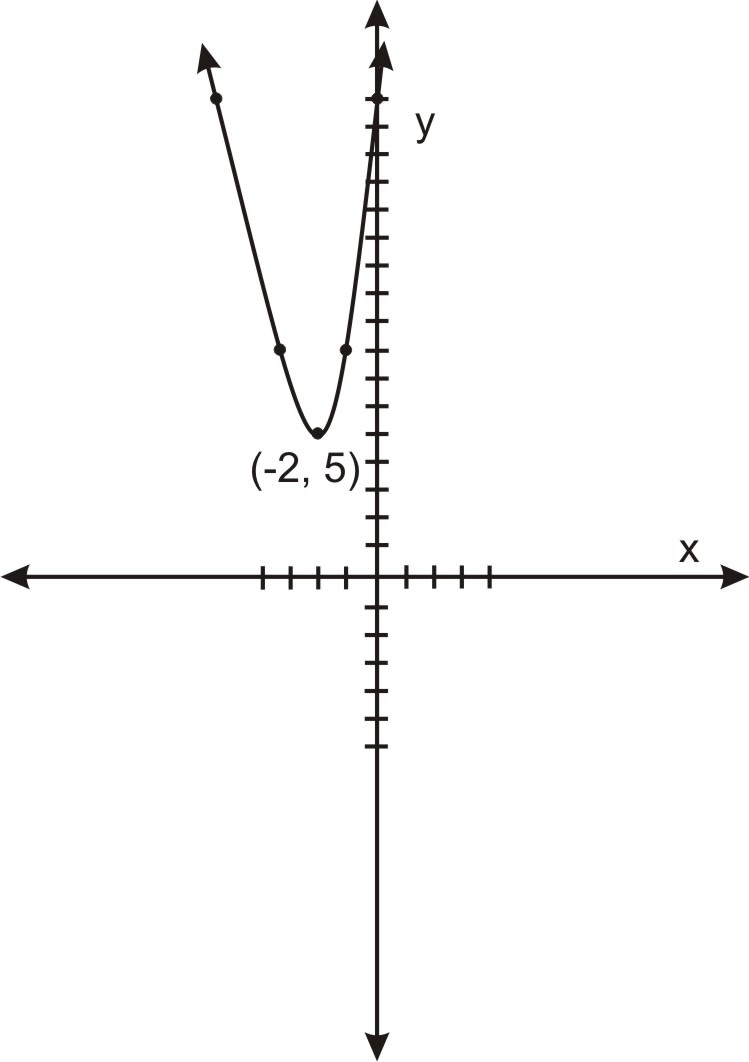
Намалюйте графік наступної параболи:\(\ y=2 x^{2}-2 x-3\).
Рішення
Фактор з 2:\(\ y=2\left(x^{2}-x\right)-3\)
Завершіть квадрат:\(\ y+\frac{1}{2}=2\left(x^{2}-x+\frac{1}{4}\right)-3\)
Додайте 3 до обох сторін і введіть тріноміал:\(\ y+3 \frac{1}{2}=2\left(x-\frac{1}{2}\right)^{2}\)
Вершина\(\ (h, k)\) - це:\(\ \left(\frac{1}{2},-3 \frac{1}{2}\right)\)
Ділянка на пару очок, щоб отримати:
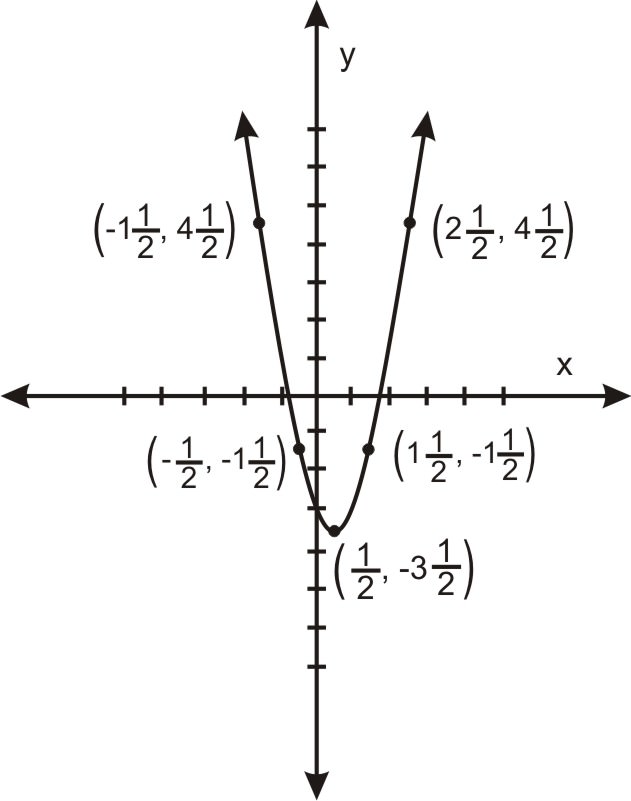
Намалюйте графік наступної параболи:\(\ 3 x^{2}+12 x+11-y=0\).
Рішення
Фактор з 3 і перемістіть y і 11:\(\ 3\left(x^{2}+4 x\right)=y-11\)
Завершіть квадрат:\(\ 3\left(x^{2}+4 x+4\right)=y-11+12\)
Фактор тріноміала і збирайте подібні терміни:\(\ 3(x+2)^{2}=y+1\)
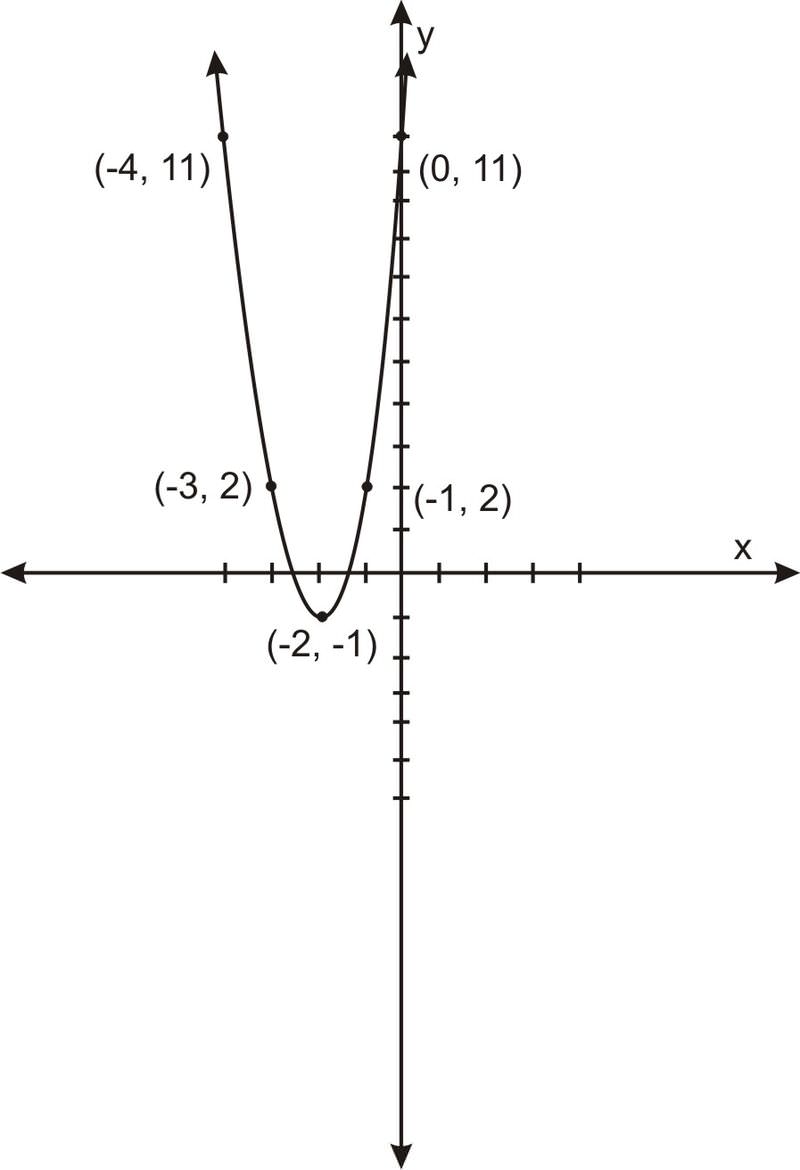
Вершина\(\ (h, k)\) знаходиться за адресою:\(\ (-2,-1)\)
Ділянка на пару очок, щоб отримати:
Визначте, які з наступних рівнянь є параболами:
- \(\ y-5 x+x^{2}=3\)
- \(\ x^{2}-3 y^{2}+3 y-2 x+15=0\)
- \(\ x-6 y^{2}+20 x-100=0\)
Рішення
Нагадаємо, що парабола має лише квадратний вхідний термін:
Оскільки\(\ \text { b. } x^{2}-3 y^{2}+3 y-2 x+15=0\) знаходиться в квадраті на вході і виході (іншими словами, обидва\(\ x\) і\(\ y\) знаходяться в квадраті), це не парабола.
\(\ \text { a. } y-5 x+x^{2}=3\)і\(\ \text { c. } x-6 y^{2}+20 x-100=0\) є обома параболами.
До речі, після завершення квадрата, рівняння а множники, такі як:
\(\ (x-1)^{2}-3\left(y-\frac{1}{2}\right)^{2}+14 \frac{3}{4}=0\).
Обчисліть відстань між (3, 4) і (9, 5).
Рішення
Для обчислення відстані між (3, 4) і (9, 5) скористайтеся формулою відстані
\(\ \text { distance }=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(\ \text { distance }=\sqrt{(9-3)^{2}+(5-4)^{2}} \ldots . . \text { Substitute }\)
\(\ \text { distance }=\sqrt{(6)^{2}+(1)^{2}} \ldots . . \text { Simplify }\)
\(\ \text { distance }=\sqrt{36+1} \rightarrow \sqrt{37}\)
\(\ \therefore \sqrt{37}\)відстань між (3, 4) і (9, 5).
Обчисліть відстань між (-2, 7) і (11, 23).
Рішення
Для обчислення відстані між (-2, 7) і (11, 23) скористайтеся формулою відстані
\(\ \text { distance }=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(\ \text { distance }=\sqrt{(11-(-2))^{2}+(23-7)^{2}} \ldots . . \text { Substitute }\)
\(\ \text { distance }=\sqrt{(13)^{2}+(16)^{2}} \ldots . . \text { Simplify }\)
\(\ \text { distance }=\sqrt{169+256} \rightarrow \sqrt{425} \rightarrow 5 \sqrt{17}\)
\(\ \therefore 5 \sqrt{17}\)відстань між (-2, 7) і (11, 23).
Рецензія
Графік наступний:
- \(\ y=-3(x-1)^{2}+2\)
- \(\ y=3(x-1)^{2}-1\)
- \(\ x=-2(y+2)^{2}-1\)
- \(\ y=3(x+4)^{2}-1\)
- \(\ y=(x-3)^{2}\)
- \(\ x=-3(y)^{2}+1\)
- \(\ x=-(y-3)^{2}-4\)
- \(\ x=-3(y-4)^{2}+4\)
- \(\ y=2(x+3)^{2}-3\)
- \(\ x=(y-1)^{2}-2\)
Для питань 11-20 уявіть обмежений конус (не нескінченно високий), як на фото нижче. Припустимо, що дві перераховані координати представляють перетин параболічної кривої та вершини конуса. Якби верхня поверхня конуса була представлена віссю x, то дві координати можна було б вважати x -перехопленнями рівняння параболи. Знайдіть відстань між точками, а там, де потрібно, координати точок.
- Координати: (-20, -17) і (6, -1)
- Координати: (-1, -5) і (6, -13)
- Координати: (1, 2) і (5, -5)
- Координати: (13, 12) і (15, 6)
- Координати: (3, 9) і (6, -14)
- \(\ -25 x^{2}+15 x+10=0\)
- \(\ -24 x^{2}+22 x-4=0\)
- \(\ 4 x^{2}-24 x+32=0\)
- \(\ 24 x^{2}+54 x+27=0\)
- \(\ 12 x^{2}+25 x+12=0\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.3.
Лексика
| Термін | Визначення |
|---|---|
| Конгруентний | Конгруентні фігури ідентичні за розміром, формою і мірою. |
| директриса | Директриса параболи - це лінія, від якої парабола, здається, крива. Всі точки на параболі рівновіддалені від вогнища параболи і директриси параболи. |
| Формула відстані | Відстань між двома точками\(\ \left(x_{1}, y_{1}\right)\) і\(\ \left(x_{2}, y_{2}\right)\) може бути визначено як\(\ d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\). |
| Еліпс | Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами. |
| еліпси | Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами. |
| фокус | У центрі уваги параболи є точка, яка «закріплює» параболу. Будь-яка точка на параболі знаходиться точно на такій же відстані від фокуса, як і від директриси. |
| Парабола | Парабола - це множина точок, що знаходяться на рівній відстані від фіксованої точки внутрішньої кривої, яка називається «'focus"', і лінія на зовнішній стороні, яка називається «'directrix"'. Директриса буває вертикальною або горизонтальною, в залежності від орієнтації параболи. |
| Вершина | Вершина параболи - найвища або найнижча точка на графіку параболи. Вершина - це максимальна точка параболи, яка відкривається вниз, і мінімальна точка параболи, яка відкривається вгору. |