5.2.3: Перехресні вироби

Перехресні вироби

Перехресні продукти пов'язані з точковими продуктами в ряді способів. Обидва є векторними розрахунками, обидва пов'язані не тільки з величиною кожного вектора, але і з відносними напрямками обох векторів.

Точкові добутки в певному сенсі обчислюють об'єднану силу двох векторів у заданому напрямку, і тому найбільші, коли вектори паралельні. Поперечні продукти, однак, найбільші, коли вектори перпендикулярні... що тоді вони обчислюють?

---

Перехресні вироби

Тоді як крапковий добуток двох векторів створює скалярне значення; перехресний добуток тих же двох векторів створює векторну величину, яка має напрямок, перпендикулярний початковим двом векторам.

Перехресний добуток двох векторних величин - це інший вектор, величина якого змінюється у міру зміни кута між двома початковими векторами. Перехресний добуток іноді називають векторним добутком двох векторів. Величина перехресного добутку являє собою площу паралелограма, сторони якого визначаються двома векторами, як показано на малюнку нижче. Тому максимальне значення для перехресного добутку виникає, коли два вектори перпендикулярні один одному, але коли два вектори паралельні один одному, величина перехресного добутку дорівнює нулю.

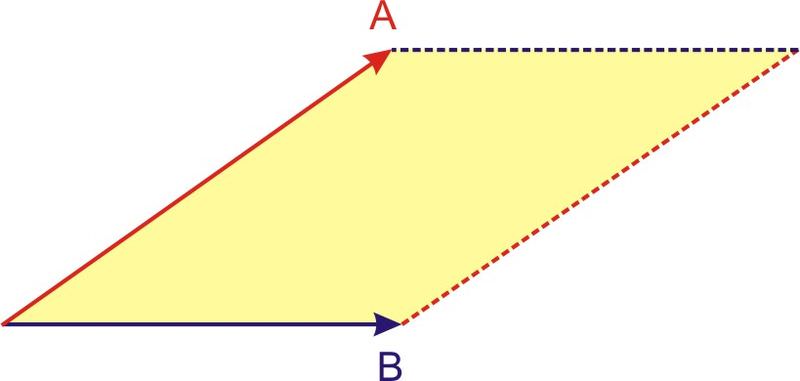
Алгебраїчна форма рівняння перехресного добутку складніша, ніж для точкового добутку. Для двох 3D векторів\(\ \vec{A}\) і\(\ \vec{B}\),

\(\ \vec{A} \times \vec{B}=\left\langle\left(A_{2} B_{3}-A_{3} B_{2}\right),\left(A_{3} B_{1}-A_{1} B_{3}\right),\left(A_{1} B_{2}-A_{2} B_{1}\right)\right\rangle\)

Інший спосіб опису процесу полягає в тому, щоб сказати, що перехресний добуток - це множення одного вектора на компонент іншого вектора, який перпендикулярний першому вектору. На схемі нижче два вектори, A і B. Перпендикулярна лінія була проведена радіально назовні від B до A, щоб створити прямокутний трикутник з A як гіпотенузою.

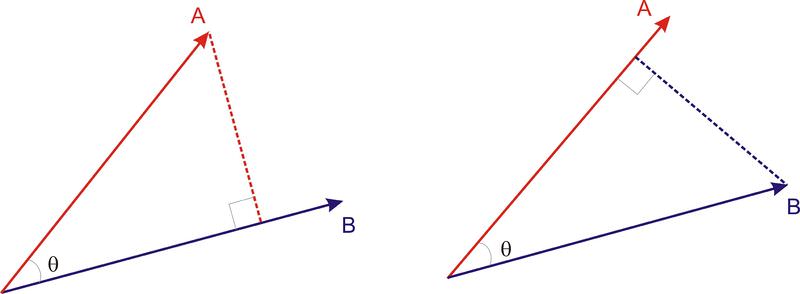
Компонент\(\ \vec{A}\) якого перпендикулярний,\(\ \vec{B}\) задається A sin θ, тому величину перехресного добутку можна записати як\(\ |\vec{A} \times \vec{B}|=\vec{A}(\vec{B} \sin \theta)=|\vec{A}||\vec{B}| \sin \theta\)

Напрямок поперечного добутку перпендикулярно площині, визначеній двома схрещеними векторами. Наприклад, перехресний добуток двох векторів в площині x-y буде паралельно осі z. Це все ще залишає два можливі напрямки для перехресного добутку: або +або −.

Використовуємо правилом для позначення напрямку поперечного виробу. Розмістіть великий і вказівний пальці правої руки першим вектором уздовж великого пальця, а другий вектор уздовж вказівного пальця. Ваш середній палець при розширенні перпендикулярно долоні вкаже напрямок перехресного добутку двох векторів.

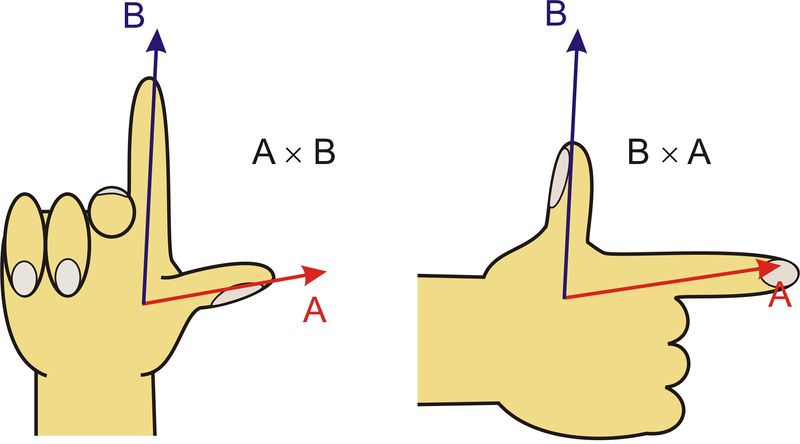
Як ви можете бачити на схемі вище,\(\ \vec{A} \times \vec{B}\) знаходиться вздовж +( виходить зі сторінки), поки\(\ \vec{B} \times \vec{A}\) знаходиться уздовж −( спускаючись на сторінку) і\(\ \vec{A} \times \vec{B}=-\vec{B} \times \vec{A}\)

Нормальний вектор

Ми можемо використовувати перехресний добуток і визначення вектора одиниці для визначення напрямку, який перпендикулярний площині.

Загалом, ми можемо визначити нормальний вектор, n, який має одиничну величину (тобто величину, рівну одиниці) і який перпендикулярний площині, зайнятій парою векторів, U і V.

\(\ \hat{n}=\frac{\vec{U} \times \vec{V}}{|\vec{U} \times \vec{V}|}\)

---

Приклади

Приклад 1

Обчисліть перехресний добуток двох векторів, показаних нижче.

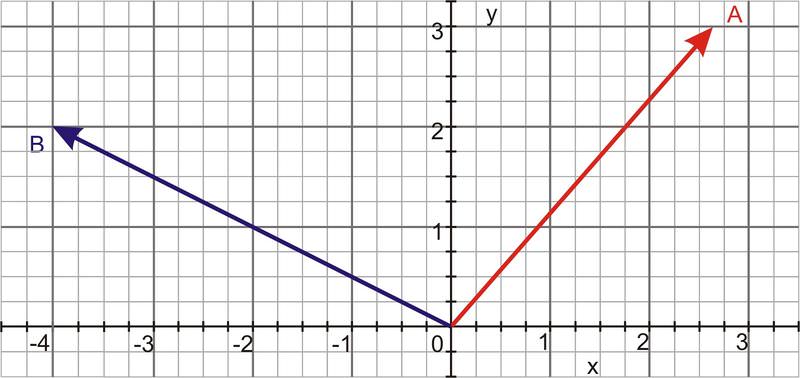
Рішення

Використовуйте компоненти двох векторів для визначення перехресного добутку.

\(\ \vec{A} \times \vec{B}=\left\langle\left(A_{y} B_{z}-A_{z} B_{y}\right),\left(A_{z} B_{x}-A_{x} B_{z}\right),\left(A_{x} B_{y}-A_{y} B_{x}\right)\right\rangle\)

Оскільки ці два вектори знаходяться в площині x-y, їх власні z-складові рівні 0, а векторний добуток буде паралельний осі z.

\ (\\ почати {масив} {l}
\ vec {A}\ times\ vec {B} =\ лангол [(3\ cdot 0) - (0\ cdot 2)], [(0\ cdot-4) - (2.5\ cdot 0)], [(2.5\ cdot 2) - (3\ cdot-4)]\
діапазон\\ vec {A}\ раз\ vec {B} =\ кут [(0) - (0)], [(0) - (0)], [(5) - (-12)]\ діапазон =\ кут 0,0, (5+12)\ діапазон =\ кут 0,0,17\ кут
\ кінець { масив}\)

Ми можемо перевірити нашу відповідь, використовуючи синусоїдальну версію перехресного добутку, але спочатку нам потрібно знати кут між двома векторами. Ми можемо використовувати точковий добуток, щоб знайти θ. Спочатку використовуйте компоненти, щоб знайти точковий твір.

\(\ \vec{A} \times \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}=(2.5 *-4)+(3 * 2)+(0 * 0)=-10+6+0=-4\)

Потім знайдіть величини двох векторів:

\ (\\ почати {масив} {л}
|\ vec {A} |=\ sqrt {A_ {x} ^ {x} ^ {2} +A_ {y} ^ {z} ^ {2}} =\ sqrt {2.5^ {2} +3^ {2}} +0^ {2}} =\ sqrt {6.25+9+0} =\ sqrt {15.0} 25}\\
|\ vec {B} |=\ sqrt {B_ {x} ^ {2} +B_ {y} ^ {2} +B_ {z} ^ {2}} =\ sqrt {(-4) ^ {2} +2} +0^ {2}} =\ sqrt {16+4+0} =\ sqrt {20}\ кінець {2}} =\ sqrt {20}
\ кінець {масив})

Потім використовуйте ці величини з косинусною версією крапкового добутку, щоб знайти θ.

\ (\\ почати {масив} {l}
\ vec {A}\ times\ vec {B} =|A||B|\\ cos\ тета\\
-4=\ sqrt {15.25}\ sqrt {20}\ cos
\ тета\\ cos\ theta=\ frac {-4} {\ sqrt {305}}\ приблизно\ frac {-4}\
\ тета=103^ {\ circ}
\ кінець {масив}\)

Тепер використовуйте синус цього кута і дві величини для визначення перехресного добутку:

\ (\\ почати {масив} {л}
|\ vec {A}\ times\ vec {B} |=|\ vec {A} ||\ vec {B} |\ sin\ тета\\ |\ vec {A}\ times\ vec {B} |=\ sqrt {15.25}\ sqrt {20}\ sin 103^ {\ circ} =\ sqrt {305}\ sqrt {15}\ sqrt {20}\ sin 103^ {\ circ} =\ sqrt {305}\ sin 103^ {\ circ} =17
\ кінець {масив}\)

Це та сама відповідь, яку ми отримали з позначення компонента, що добре. Використовуємо правило правої руки для визначення напрямку векторного добутку. Якщо розмістити великий палець уздовж вектора А, а вказівний палець уздовж вектора B, середній палець буде вказувати вздовж +і\(\ |\vec{A} \times \vec{B}|=\langle 0,0,17\rangle\)

Приклад 2

На діаграмі показані два вектори A і B, які визначають площину, що проходить через початок. Скористайтеся цими двома векторами для визначення вектора нормалі до цієї площини. \(\ \vec{A}=\langle 3,0,4\rangle\)і\(\ \vec{B}=\langle 5,10,0\rangle\)

Рішення

Нормальний вектор визначається

\(\ \hat{n}=\frac{\vec{U} \times \vec{V}}{|\vec{U} \times \vec{V}|}\)

В цьому випадку отримуємо

\(\ \hat{n}=\frac{\vec{A} \times \vec{B}}{|\vec{A} \times \vec{B}|}\)

Використовуйте компонентну версію рівняння крос-добутку для пошуку компонентів\(\ \vec{A} \times \vec{B}\)

\ (\\ begin {масив} {l}
\ vec {A}\ times\ vec {B} =\ лівий\ кут\ лівий (A_ {y} B_ {z} -A_ {z} B_ {z}\ праворуч),\ лівий (A_ {z} B_ {x} -A_ {x} B_ {z}\ праворуч),\ лівий (A_ {z} B_ {x} _ {y} -A_ {y} B_ {x}\ право)\ право\ діапазон\\ vec {A}\ час\ vec {B} =
\ кут [(0\ cdot 0) - (4\ cdot 10)], [(4\ cdot 5) - (3\ cdot 0)], [(3\ cdot 10) - (0\ cdot 10) - (0\ cdot 5) - (3\ cdot 0) - (0\ cdot 5)]\ діапазон\
\ vec {A}\ times\ vec {B} =\ лангл (0-40), (20-0), (30-0)\ діапазон =\ ланг-40,20,30\ діапазон
\ кінець {масив}\)

Далі обчислюємо величину перехресного добутку,\(\ |\vec{A} \times \vec{B}|\)

\ (\\ почати {масив} {л}
|\ vec {A}\ times\ vec {B} |=\ sqrt {(-40) ^ {2} +20^ {2} +30^ {2}} =\ sqrt {1600+400+900} =\ sqrt {2900} =53.8516\
\ капелюх {n} =\ frac {vec {A} раз\ vec {B}} {|\ vec {A}\ times\ vec {B} |} =\ frac {\ ланг-40,20,30\ діапазон} {53.9} =\ лівий\ лангель\ frac {-40} {53.9},\ frac {20} {53.9},\ frac {30} {53.9} праворуч\ діапазон =\ лангу-0.743,0.371,0.557\ діапазон
\ кінець {масив}\)

Приклад 3

Визначте перехресний\(\ \vec{F} \times \vec{r}\) добуток для двох векторів\(\ \vec{F}=\langle 2,3,4\rangle\) і\(\ \vec{r}=\langle 7,6,5\rangle\). Потім за допомогою перехресного добутку визначити кут між двома векторами.

Рішення

Один із двох способів визначення величини перехресного добутку двох векторів використовує складові двох векторів:

\ (\\ почати {масив} {l}
\ vec {F}\ times\ vec {r} =\ лівий\ кут\ лівий (F_ {y} r_ {z} -F_ {z} r_ {z}\ правий),\ лівий (F_ {z} r_ {x} -F_ {x} r_ {z}\ правий),\ лівий (F_ {x} _ {y} -F_ {y} r_ {x}\ право)\ вправо\ діапазон\
\ vec {F}\ раз\ vec {r} =\ кут (3\ cdot 5-4\ cdot 6), (4\ cdot 7-2\ cdot 5), (2\ cdot 6-3\ dot 7)\ діапазон =\ ланґль (15-24), (28-10), (12-21)\ діапазон\
\ vec {F}\ times\ vec {r} =\ ланг-9,18, -9\ діапазон
\ кінець {масив}\)

Тепер ми можемо використовувати перехресний добуток і друге визначення перехресного добутку для визначення кута між двома векторами.

\(\ |\vec{F} \times \vec{r}|=|F||r| \sin \theta\)

Нам потрібно обчислити величини векторів і перехресного добутку.

\ (\\ почати {масив} {л}
|\ vec {F} |=\ sqrt {F_ {x} ^ {x} ^ {2} +F_ {y} ^ {z} ^ {2}} =\ sqrt {2^ {2} +3^ {2} +4^ {2}}} =\ sqrt {4+9+16} =\ sqrt {29} =5.385\\
|\ vec {r} |=\ sqrt {r_ {x} ^ {2} +r_ {y} ^ {2} +r_ {z} ^ {2}} =\ sqrt {7^ {2} +6^ {2}} =\ sqrt {49+36+25} =\ sqrt {110} =10.488\\
vec {F}\ раз\ vec {r} |=\ sqrt {(-9 ) ^ {2} +18^ {2} + (-9) ^ {2}} =\ sqrt {81+324+81} =\ sqrt {486} =22.0454\
\ sin\ theta=\ frac {|\ frac {| |} {{f||r|} =\ frac {22.0454} {(5.0454} 385) (10.488)} = 0,390\\ тета=
\ sin ^ {-1} (0.390) =22,98^ {\ circ}
\ кінець {масив}\)

Ми можемо використовувати точковий добуток двох векторів, щоб перевірити наше рішення.

\ (\\ почати {масив} {л}
\ vec {F}\ раз\ vec {r} =|\ vec {F}\ |\ vec {r} |\ cos\ тета\\ vec {F}
\ раз\ vec {r} =F_ {x} r_ {x} +F_ {y} r_ {y} +F_ {y} +F_ {y} +F_ {y} +F_ {y} +F {z} r_ {z} =2 * 7+3 * 6+4 * 5=14+18+20=52
\\ cos\ theta=\ frac {\ vec {F}\ раз\ vec {r}} {|\ vec {F} ||\ vec {r} |} =\ frac {52} {(5.385) (10.488)}} =0.920714 \
\ тета=\ cos ^ {-1} (0.920714) =22.97
\ кінець {масив}\)

Ця відповідь відповідає нашому значенню від перехресного добутку до варіацій округлення.

Приклад 4

Визначте величину перехресного добутку двох векторів, показаних нижче.

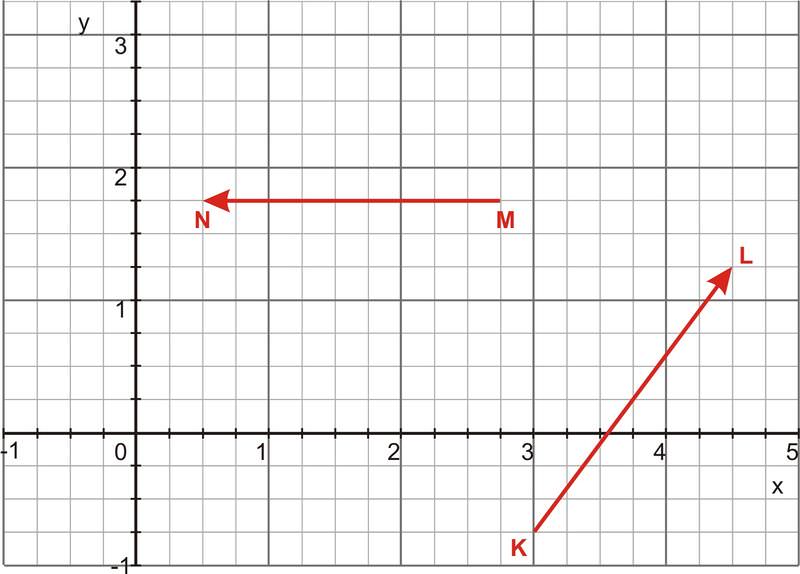
Рішення

Спочатку нам потрібно визначити складові двох векторів за допомогою інформації, наведеної на графіку. У цьому випадку\(\ \overrightarrow{M N}=\langle-2.25,0,0\rangle\) і\(\ \overrightarrow{K L}=\langle 1.5,2,0\rangle\)

\ (\\ begin {масив} {l}
\ переправа стрілка {M N}\ раз\ переправа стрілка {K L} =\ лівий\ кут\ ліворуч (M N_ {y} K L_ {z} -M N_ {z} K L_ {y}\ праворуч),\ ліворуч (M N_ {z} K L_ {x} -М {x} K {x} {z}\ праворуч),\ ліворуч (M N_ {x} K L_ {y} -M N_ {y} K L_ {x}\ праворуч)\ правий\ діапазон\
\ overrightarrow {M N}\ раз\ переправо {K L} =\ кут (0\ cdot 0-0\ cdot 2), (0\ cdot 1.5- (-2.25)\ cdot 0), ((-2.25)\ точка 2-0\ точка 1.5)\ діапазон
\\ стрілка направо {M N}\ час\ переправа {K L} =\ кут 0-0,0-0, -4.5-0\ діапазон =\ l0,0, -4.5\ діапазон
\ кінець {масив}\)

Як ми бачимо з компонентів, цей вектор має величину 4,5 одиниці і лежить у напрямку —z. Ми також можемо скористатися правилом правої руки, щоб побачити напрямок перехресного виробу. Як показано на малюнку нижче, якщо вирівняти великий палець правої руки з вектором MN і правий вказівний палець з вектором KL, долоню і витягнутий середній палець вказують в напрямку —z.

Приклад 5

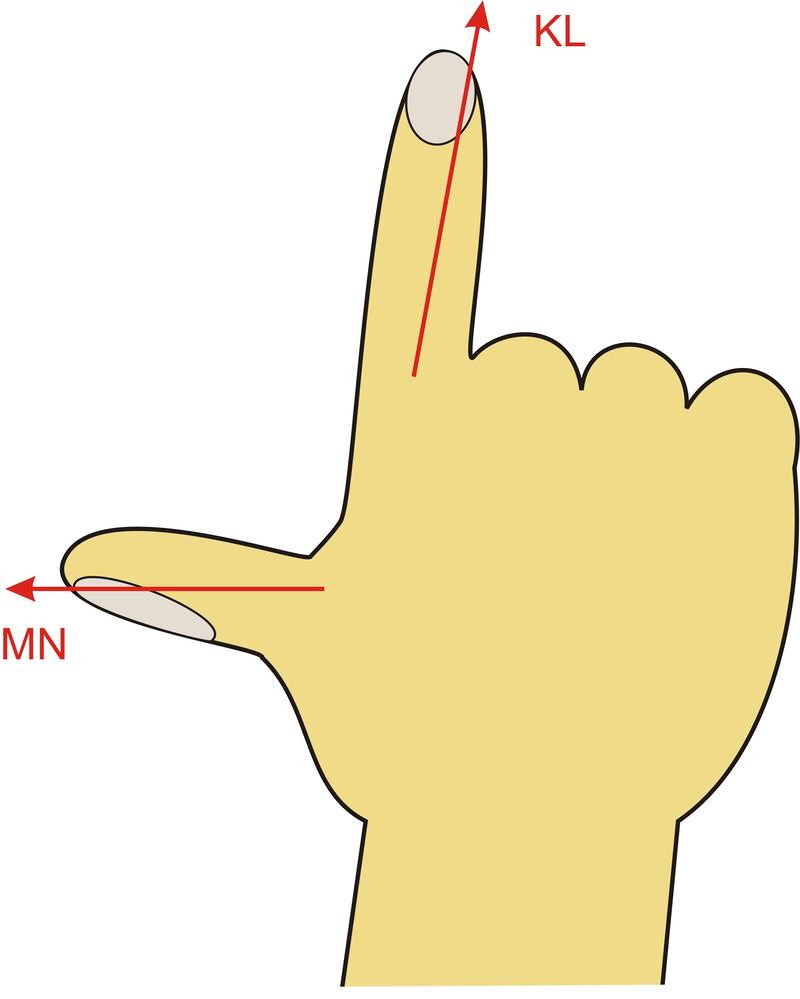
Площина, що проходить через початок, визначається двома векторами,\(\ \vec{W}=\langle 4,5,2\rangle\) і\(\ \vec{L}=\langle 8,1,9\rangle\). Визначте рівняння одиничного вектора, що представляє напрямок, перпендикулярний цій площині.

Рішення

Для вирішення цієї задачі потрібно використовувати визначення вектора нормалі\(\ \hat{n}=\frac{\vec{W} \times \vec{L}}{|\vec{W} \times \vec{L}|}\), складової форми визначення перехресного добутку,

\ (\\ почати {вирівняний}
&\ vec {W}\ times\ vec {L} =\ лівий\ кут\ лівий\ лівий (W_ {y} L_ {z} -W_ {z} L_ {z}\ правий),\ лівий (W_ {z} L_ {x} -W_ {x} L_ {z}\ праворуч),\ лівий (W_ {x} L_ {x} y} -W_ {y} L_ {x}\ правий)\ правий\ діапазон. \ text {У цьому випадку ми отримуємо}\\
&\ vec {W}\ times\ vec {L} =\ ланголь (5\ cdot 9-2\ cdot 1), (2\ cdot 8-4\ cdot 9), (4\ cdot 1-5\ cdot 8)\ діапазон\\
&\ vec {W}\ times\ vec {L} =\ langle (45-2), (16-36), (4-40)\ діапазон =\ кут 43, -20, -36\ діапазон
\ кінець {вирівняний}\)

Нам також потрібно знати величину цього перехресного добутку.

\ (\\ почати {масив} {л}
|\ vec {W}\ раз\ vec {L} |=\ sqrt {x^ {2} +y^ {2}} =\ sqrt {(43) ^ {2} + (-20) ^ {2} + (-36) ^ {2}} =\ sqrt {1849+400+1296} =\\
\ sqrt {3545} =59.54
\ кінець {масив}\)

Тепер ми можемо визначити вектор нормалі

\(\ \hat{n}=\frac{\vec{W} \times \vec{L}}{|\vec{W} \times \vec{L}|}=\frac{\langle 43,-20,-36\rangle}{59.54}=\left\langle\frac{43}{59.54}, \frac{-20}{59.54}, \frac{-36}{59.54}\right\rangle=\langle 0.7222,-0.3359,-0.6046\rangle\)

Приклад 6

Визначте площу паралелограма, сторони якого визначаються векторами\(\ \vec{w}=\langle 85,89,91\rangle\) і\(\ \vec{h}=\langle 67,70,88\rangle\), довжини вимірюються в сантиметрах.

Рішення

Площа паралелограма, сторони якого визначені парою векторів, дорівнює величині поперечного добутку двох векторів,\(\ |\vec{w} \times \vec{h}|\). Для початку нам потрібно знайти перехресний добуток двох векторів:

\ (\\ почати {масив} {l}
\ vec {w}\ times\ vec {h} =\ лівий\ кут\ лівий (w_ {y} h_ {z} -w_ {z} h_ {z}\ правий),\ лівий (w_ {z} h_ {x} -w_ {x} h_ {z}\ правий),\ лівий (w_ {z} h_ {x} _ {y} -w_ {y} h_ {x}\ право)\ право\ діапазон\
\ vec {w}\ час\ vec {h} =\ кут (89\ cdot 88-91\ cdot 70), (91\ cdot 67-85\ cdot 8), (85\ точка 70-89\ cdot 67)\ діапазон\
\ vec {w}\ час\ vec {h} =\ кут (7832-6370), (6097-7480), (5950-5963)\ діапазон =\ кут 1462, -1383, -13\ діапазон\
|\ vec {w}\ раз\ vec {h} |=\ sqrt {x^ {2} +y^ {2} +z^ {2}} =\ sqrt {1462^ {2} + (-1383) ^ {2} + (13) ^ {2}} =\ sqrt {4050302}\ приблизно 2012.5
\ кінець {масив}\)

Оскільки довжини двох векторів вимірювалися в сантиметрах, площа паралелограма становить 2013 см ², виміряна до найближчого квадратного сантиметра.

Приклад 7

Визначити перехресний добуток двох векторів\(\ \vec{f}=\langle 3,13,11\rangle\) і\(\ \vec{g}=\langle 9,6,15\rangle\)

Рішення

\ (\\ почати {масив} {l}
\ vec {f}\ times\ vec {g} =\ лівий\ кут\ лівий (f_ {y} g_ {z} -f_ {z} g_ {y}\ правий),\ лівий (f_ {z} g_ {x} -f_ {x} g_ {z}\ праворуч),\ лівий (f_ {x} g_ {x} g_ {z}\ правий),\ лівий (f_ {x} _ {y} -f_ {y} g_ {x}
\ право)\ право\ діапазон\\ vec {f}\ раз\ vec {g} =\ кут (13\ крапка 15-1\ крапка 6), (1\ cdot 9-3\ cdot 15), (3\ точка 6-13\ точка 9) \ діапазон\
\ vec {f}\ times\ vec {g} =\ лангель (195-66), (99-45), (18-117)\ діапазон =\ ланголь 129,54, -99\ діапазон
\ кінець {масив}\)

Приклад 8

Визначте величину перехресного добутку цих двох векторів.

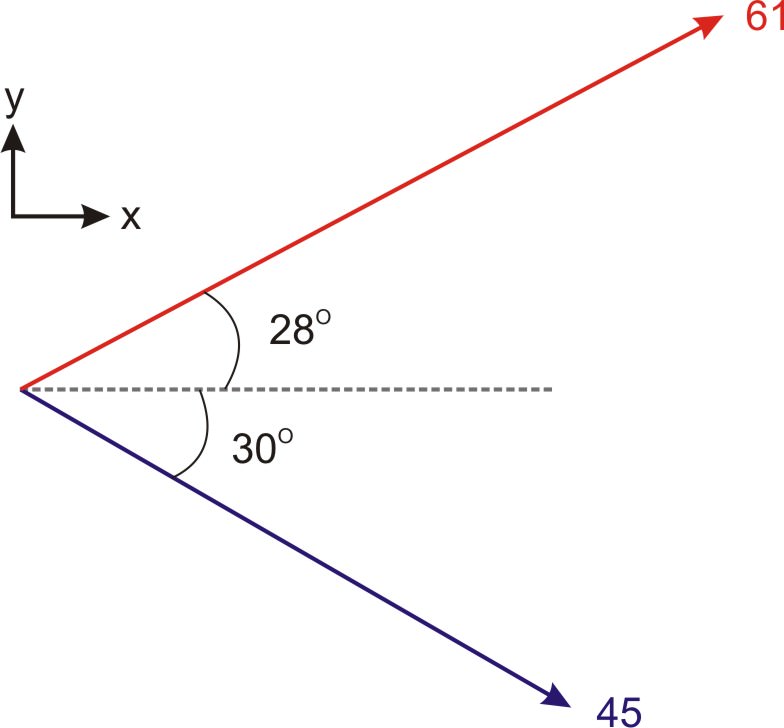
Рішення

Оскільки нам відомі величини двох векторів і кут між ними, ми можемо використовувати кут-версію рівняння перехресного добутку для визначення величини перехресного добутку:

\(\ |\vec{A} \times \vec{B}|=|\vec{A}||\vec{B}| \sin \theta=(61)(45) \sin 58=2328\)

Оскільки ці два вектора лежать в площині x-y, напрямок поперечного добутку буде паралельно осі z.

---

Рецензія

Розрахуйте перехресні вироби:

1. Вектори\(\ c=-6 i+2 j+3 k\) та\(\ a=-6 i+2 j+13 k\)
2. Вектори\(\ v=\langle-1,4,7\rangle\) та\(\ u=\langle-5,10,3\rangle\)
3. Вектори\(\ f=-6 i+8 j-6 k\) та\(\ s=-3 i+15 j+19 k\)
4. Вектори\(\ \mathrm{j}=-3 i+15 j-4 k\) та\(\ \mathrm{t}=7 i+10 j+6 k\)
5. Вектори\(\ r=\langle 3,13,-1\rangle\) та\(\ v=\langle 7,6,1\rangle\)
6. Вектори\(\ e=\langle-1,8,-3\rangle\) та\(\ a=\langle-2,1,19\rangle\)
7. Вектори\(\ \mathrm{j}=-3 i+17 j+6 k\) та\(\ h=8 i+9 j+7 k\)
8. Вектори\(\ a=9 i+10 j+9 k\) та\(\ g=-5 i+19 j+15 k\)
9. Вектори\(\ \mathrm{j}=4 i+18 j-8 k\) та\(\ m=2 i+j+19 k\)
10. Що таке перехресний твір\(\ \langle-2,1,-2\rangle\) і\(\ \langle 5,6,9\rangle\)?
11. Знайти вектор, ортогональний обох\(\ \langle 1,20,2\rangle\) і\(\ \langle 4,2,3\rangle\)
12. Вектори\(\ y=5 i+6 j+6 k\) і\(\ f=-4 i+9 j+3 k\). Яка площа паралелограма, утвореного наявністю y і f в якості суміжних сторін?
13. Яка площа паралелограма, утвореного наявністю\(\ \langle-2,1,7\rangle\) і в\(\ \langle 5,7,16\rangle\) якості суміжних сторін?
14. Що таке перехресний продукт між\(\ \langle 8,6,8\rangle\) і\(\ \langle 8,6,8\rangle\)?
15. Вектори\(\ g=-6 i+9 j-7 k\) і\(\ y=-24 i+36 j-28 k\) Що таке перехресний добуток між g та y?
16. Човен пливе на підшипнику 89° на схід від півночі в 564 футів на хвилину. Хвостовий вітер збільшує швидкість літака і дме 78° на захід від півночі зі швидкістю 25 футів на хвилину. Визначте фактичну швидкість літака в миль/год.
17. Літак летить на підшипнику 77° на схід від півдня зі швидкістю 606 миль/год. Хвостовий вітер збільшує швидкість літака і дме 33° на захід від півдня зі швидкістю 80 миль/год. Визначте напрямок площини.

---

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.6.

---

Лексика

Термін	Визначення
перехресний продукт	Перехресний добуток двох векторів - це третій вектор, який перпендикулярний обом вихідним векторам.
точковий добуток	Точковий добуток також відомий як внутрішній продукт або скалярний продукт. Дві форми точкового добутку є\(\ \vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta\) і\(\ \vec{a} \cdot \vec{b}=x_{a} x_{b}+y_{a} y_{b}\)
нормальний вектор	Нормальний вектор - це вектор, який перпендикулярний заданій поверхні або площині. Одиничний вектор нормалі - це нормальний вектор з величиною одиниці.
Правило праворуч	Правило правої руки використовується для позначення напрямку поперечного виробу. Розмістіть великий і вказівний пальці правої руки першим вектором уздовж великого пальця, а другий вектор уздовж вказівного пальця. Ваш середній палець при розширенні перпендикулярно долоні вкаже напрямок перехресного добутку двох векторів.
одиниця вектор	Одиничний вектор - це вектор з величиною одиниці.