5.2.1: Точкові продукти

Точковий добуток і кут між двома векторами

Хоча два вектори не можна суворо множити, як можуть числа, існує два різні способи знайти добуток між двома векторами. Перехресний добуток між двома векторами призводить до створення нового вектора, перпендикулярного іншим двом векторам. Ви можете дізнатися більше про перехресний добуток між двома векторами, якщо взяти Лінійну алгебру. Другим типом добутку є крапковий добуток між двома векторами, що призводить до регулярного числа. Інші назви крапкового добутку включають внутрішній добуток і скалярний добуток. Це число позначає, скільки одного вектора йде в напрямку іншого. В одному сенсі він вказує на те, наскільки два вектори узгоджуються один з одним. Ця концепція буде зосереджена на точковий добуток між двома векторами.

Що таке крапковий добуток між <−1,1> і <4,4>? Що означає результат?

---

Властивості точкового добутку

Точковий добуток визначається як:\(\ u \cdot v=<u_{1}, u_{2}>\cdot<v_{1}, v_{2}>=u_{1} v_{1}+u_{2} v_{2}\)

Ця процедура говорить про те, що ви множите відповідні значення, а потім підсумовуєте отримані продукти. Він може працювати з векторами, які мають більше двох вимірів однаково.

Перш ніж спробувати цю процедуру з конкретними числами, подивіться на наступні пари векторів та відносні оцінки їх крапкового добутку.

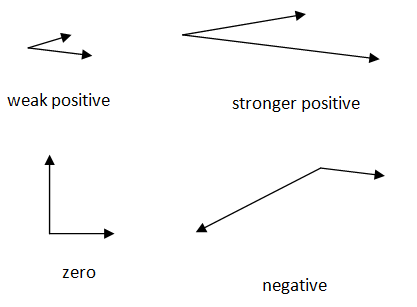
Зверніть увагу, як вектори, що йдуть в загальному тому ж напрямку, мають позитивний добуток точки. Подумайте про дві сили, що діють на один об'єкт. Позитивний точковий добуток означає, що ці сили працюють разом хоча б трохи. Інший спосіб сказати, що це кут між векторами менше 90 ^o.

Існує багато важливих властивостей, пов'язаних з точковим добутком. Двома найважливішими є 1) що відбувається, коли вектор має крапковий добуток з собою і 2) що є точковим добутком двох векторів, які перпендикулярні один одному.

• \(\ v \cdot v=|v|^{2}\)
• \(\ v\)і\(\ u\) перпендикулярні тоді і тільки якщо\(\ v \cdot u=0\)

Комутативна властивість утримує крапковий добуток між двома векторами.\(\ u \cdot v=v \cdot u\) Наступний доказ є для двовимірних векторів, хоча це стосується будь-яких розмірних векторів.

Почніть з векторів у вигляді компонента.

\ (\\ begin {масив} {l}
u=<u_ {1}, u_ {2} >\\
v=<v_ {1}, v_ {2} >
\ кінець {масив}\)

Потім застосуйте визначення точкового добутку та переставте терміни. Комутативна властивість вже відома для регулярних чисел, тому ми можемо використовувати це.

\ (\\ почати {вирівняний}
u\ cdot v &=\ лівий\ кут u_ {1}, u_ {2} >\ cdot<v_ {1}, v_ {2} >\ праворуч. \\
&=u_ {1} v_ {1} +u_ {2} v_ {2}\\
&=v_ {1} u_ {1} +v_ {2} u_ {2}\\
&= \<v_ {1}, v_ {2} > cdot \<u_ {1}, u_ {2} >\
&= v\ cdot u
\ кінець {вирівняний}\)

Розподільна властивість u⋅ (v+w) = uv+uw, також тримається під точковим добутком. Наступний доказ буде працювати з двовимірними векторами, хоча властивість має взагалі.

\ (\\ почати {вирівняний}
u=<u_ {1}, u_ {2} >, v=<v_ {1}, v_ {2} >, w &=\ лівий\ кут w_ {1}, w_ {2}\ правий\ діапазон\\
u\ cdot (v+w) &= u\ cdot\ ліво+ <v_ {1}, v_ {2} > \<w_ {1}, w_ {2} > вправо)\\ &= u
\ cdot<v_ {1} +w_ {1}, v_ {2} +w_ {2} >\\ &= <u_
{1}, u_ {2} >\ cdot<v_ {1} +w_ {1}, v_ {2} +w_ {2} >\\
&=u_ {1}\ лівий (v_ {1} +w_ {1}\ праворуч) +u_ {2}\ лівий (v_ {2} +w_ {2}\ праворуч)\\
&=u_ {1} v_ {1} +u_ {1} w_ {1} +u_ {2} v_ {2} +u_ {2} +u_ {2} _ {2} w_ {2}\\
&=u_ {1} v_ {1} +u_ {2} v_ {2} +u_ {1} w_ {1} +u_ {2} w_ {2}\\
&=u\ cdot v+v\ cdot w
\ end {вирівняний}\)

Точковий добуток може допомогти вам визначити кут між двома векторами, використовуючи наступну формулу. Зверніть увагу, що в чисельнику потрібно точковий добуток, оскільки кожен член є вектором. У знаменнику потрібно лише регулярне множення, оскільки величина вектора - це лише звичайне число, що вказує довжину.

\(\ \cos \theta=\frac{u \cdot v}{|u||v|}\)

Перегляньте частину цього відео, зосереджуючись на точковий продукт:

---

Приклади

Приклад 1

Раніше вам було запропоновано знайти точковий добуток між двома векторами <−1,1> і <4,4>.

Рішення

Його можна обчислити як:

(−1) (4) +1 (4) =−4+4=0

Результат нуля має сенс, оскільки ці два вектори перпендикулярні один одному.

Приклад 2

Знайдіть добуток крапки між наступними векторами: <3,1>⋅<5, −4>

Рішення

\(\ u\)=<3,5>

Приклад 3

Доведіть формулу кута між двома векторами:

\(\ \cos \theta=\frac{u \cdot v}{|u||v|}\)

Рішення

Почніть з закону затишку.

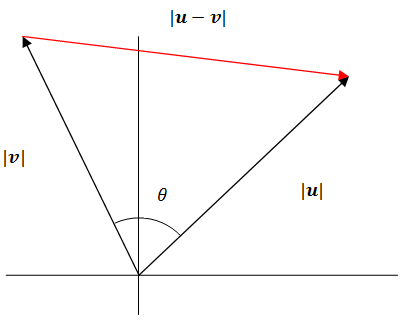
\ (\\ почати {вирівняний}
|u-v|^ {2} &=|v|^ {2} +|u|^ {2} -2|v||u|\ cos\ тета\\ (u-v)\ cdot
(u-v)\ cdot (u-v) &=\\
u\ cdot u-2 u\ cdot v+v\ cdot v &=\\
u|^ {2} -2 u\ cdot v+v\ cdot v &=\\ u|^ {2} точка v+|v|^ {2} &=\\
-2 u\ cdot v &=-2|v||u|\ cos\ тета\
\ гідророзриву {u\ cdot v} {|u||v|} &=\ cos\ тета
\ кінець {вирівняний}\)

Приклад 4

Знайдіть крапковий добуток між наступними векторами.

\(\ (4 i-2 j) \cdot(3 i-8 j)\)

Рішення

Стандартні одиничні вектори можуть бути записані як складові вектори.

\(\ <4,-2>\cdot<3,-8>=12+(-2)(-8)=12+16=28\)

Приклад 5

Що таке кут між\(\ u=<3,5>\) і\(\ v=<2,8>\)?

Рішення

Використовуйте формулу кута між двома векторами.

\(\ u=<3,5>\text { and } v=<2,8>\)

\ (\\ почати {вирівняний}
\ frac {u\ cdot v} {|u||v|} &=\ cos\ тета\
\ frac {<3,5>\ cdot<2,8>} {\ sqrt {34}\ cdot\ sqrt {68}} &=\ cos\ тета\
\ frac {6+40} {\ sqrt {34}\ cdot\ sqrt {68}} &=\ cos\ тета\
\ cos ^ {-1}\ лівий (\ frac {46} {\ sqrt {34}\ cdot\ sqrt {68} }\ праворуч) &=\ тета\\
16.93^ {\ circ} &\ приблизно\ тета
\ кінець {вирівняний}\)

---

Рецензія

Знайдіть крапковий добуток для кожної з наступних пар векторів.

1. <2,6>⋅<−3,5>
2. <5, −1>⋅<4,4>
3. <−3, −4>⋅<2,2>
4. <3,1>⋅<6,3>
5. <−1,4>⋅<2,9>

Знайдіть кут між кожною парою векторів нижче.

6. <2,6>⋅<−3,5>
7. <5, −1>⋅<4,4>
8. <−3, −4>⋅<2,2>
9. <3,1>⋅<6,3>
10. <−1,4>⋅<2,9>
11. Що таке\(\ v \cdot v\)?
12. Як можна використовувати точковий добуток, щоб знайти величину вектора?
13. Що таке\(\ 0 \cdot v\)?
14. Покажіть,\(\ c\) що\(\ (c u) \cdot v=u \cdot(c v)\) де константа.
15. Показати, що <2,3> перпендикулярно <1.5, −1>.

---

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 7.4.

---