5.2.4: Векторна проекція
- Page ID
- 55166
Векторна проекція
Проектування одного вектора на інший явно відповідає на питання: «скільки одного вектора йде в напрямку іншого?» Точковий добуток корисний тим, що він виробляє скалярну величину, яка допомагає відповісти на це питання. У цій концепції ви створите фактичний вектор, а не просто скаляр.
Чому векторна проекція корисна при розгляді витягування коробки в напрямку,\(\ v\) а не горизонтально в напрямку\(\ u\)?
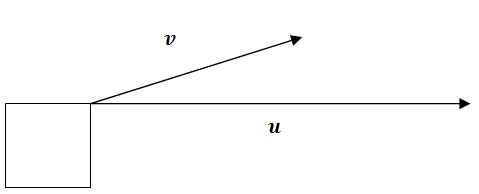
Проекції
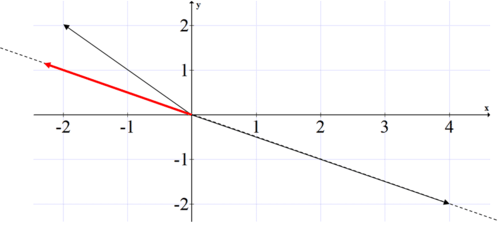
Розглянемо питання зверху.
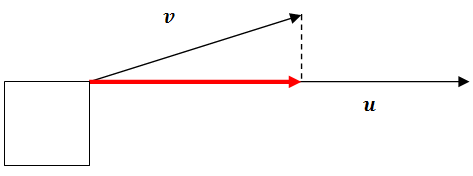
Визначення векторної проекції для зазначеного червоного вектора називається\(\ \operatorname{proj}_{u} v\). Коли ви\(\ \operatorname{proj}_{u} v\) читаєте, ви повинні сказати «векторну проекцію\(\ v\) на»\( u\). Це означає, що новий вектор йде в сторону\(\ u\). Векторна проекція - це вектор, який утворюється, коли один вектор вирішується на два складові вектори, один, який паралельний другому вектору і один, який перпендикулярний другому вектору. Паралельний вектор - векторна проекція.
Концептуально це означає, що якщо хтось тягнув коробку під кутом і силою вектора,\(\ v\) то частина їх енергії буде витрачена даремно, потягнувши коробку вгору, і частина енергії насправді сприяла б витягуванню коробки горизонтально.
Визначення скалярної проекції - це просто довжина векторної проекції. Коли скалярна проекція позитивна, це означає, що кут між двома векторами менше 90. Коли скалярна проекція негативна, це означає, що два вектори рухаються в протилежних напрямках.
Формулу векторної проекції можна записати двома способами. Версія зліва найбільш спрощена, але версія праворуч має найбільш сенс концептуально. А.
\(\ \operatorname{proj}_{u} v=\left(\frac{v \cdot u}{|u|^{2}}\right) u=\left(\frac{v \cdot u}{|u|}\right) \frac{u}{|u|}\)
Доказ формули векторної проекції полягає в наступному:
З огляду на два вектори\(\ u\)\(\ v\), що таке\(\ \operatorname{proj}_{u} v\)?
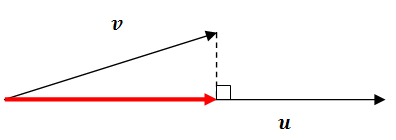
Спочатку зверніть увагу, що проектований вектор червоним кольором буде йти в напрямку\(\ u\). Це означає, що він буде добутком одиничного вектора\(\ \frac{u}{|u|}\) і довжини червоного вектора (скалярної проекції). Для того щоб знайти скалярну проекцію, зверніть увагу на прямокутний трикутник, невідомий кут θ між двома векторами і коефіцієнт косинусів.
\(\ \cos \theta=\frac{\text { scalar projection }}{|v|}\)
Нагадаємо, що\(\ \cos \theta=\frac{u \cdot v}{|u||v|}\). Тепер просто підставляємо і спростимо знайти довжину скалярної проекції.
\ (\\ почати {вирівняний}
\ cos\ тета &=\ frac {\ текст {скалярна проекція}} {|v|}
\\ розриву {u\ cdot v} {|u||v|} &=\ текст {скалярна проекція}} {|v|}\\
frac {u\ cdot v} {|u|} &=\ текст {скалярний проекція}
\ кінець {вирівняний}\)
Тепер у вас є довжина векторної проекції та напрямок, в якому ви хочете, щоб вона пройшла:
\(\ \operatorname{proj}_{u} v=\left(\frac{u \cdot v}{|u|}\right) \frac{u}{|u|}\)
Приклади
Раніше вас запитали, чому векторна проекція корисна при розгляді тягнути коробку в напрямку, а не горизонтально в напрямку\(\ u\). Векторна проекція корисна у застосуваннях фізики, що включають силу та роботу.
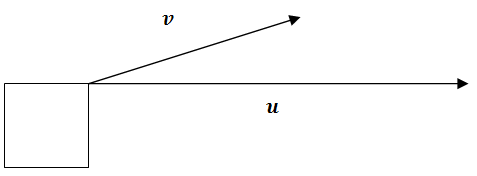
Рішення
Коли коробка витягується вектором,\(\ v\) частина сили витрачається даремно, підтягуючи проти сили тяжіння. У реальному житті це може бути корисно через тертя, але поки ця енергія неефективно витрачається на горизонтальний рух коробки.
Знайти скалярну проекцію вектора\(\ v=<3,4>\) на вектор\(\ u=<5,-12>\).
Рішення
Як зазначалося раніше, скалярна проекція - це величина векторної проекції. Це було показано,\(\ \left(\frac{u \cdot v}{|u|}\right)\) де\(\ u\) знаходиться вектор, на який проектується.
\(\ \frac{u \cdot v}{|u|}=\frac{<5,-12>\cdot<3,4>}{13}=\frac{15-48}{13}=-\frac{33}{13}\)
Знайти векторну проекцію вектора\(\ v=<3,4>\) на вектор\(\ u=<5,-12>\)
Рішення
Оскільки скалярна проекція вже була знайдена в прикладі 2, вам слід помножити скаляр на одиничний вектор «на».
\(\ -\frac{33}{13}<\frac{5}{13},-\frac{12}{13}>=<-\frac{165}{169}, \frac{396}{169}>\)
Намалюйте вектор\(\ <-2,-2>\) і\(\ <4,-2>\). Поясніть, використовуючи ескіз, чому негативна\(\ <-2,-2>\) скалярна проекція на має\(\ <4,-2>\) сенс.
Рішення
Спочатку побудуйте два вектори і продовжте вектор «на». Коли відбувається векторна проекція, вектор\(\ <-2,2>\) йде в протилежному напрямку вектора\(\ <4,-2>\). Це створить векторну проекцію, що йде в протилежному напрямку\(\ <4,-2>\).
Батько тягне дочку на пагорб. Пагорб має ухил в 20 о. Дочка на санках, що сидить на землі і має мотузку, яку батько тягне з силою 100 фунтів, коли він ходить. Канат робить кут 39 о з ухилом. Яку ефективну силу докладає батько, переміщаючи дочку і сани в гору?
Рішення
Коробка представляє дівчину і санки. Синя стрілка вказує на 100 фунтів сили батька. Зверніть увагу, що питання запитує просто кількість сили, що означає скалярну проекцію. Оскільки це не залежить від нахилу цього пагорба, ми можемо повернути нашу перспективу і все одно отримати таку ж скалярну проекцію.
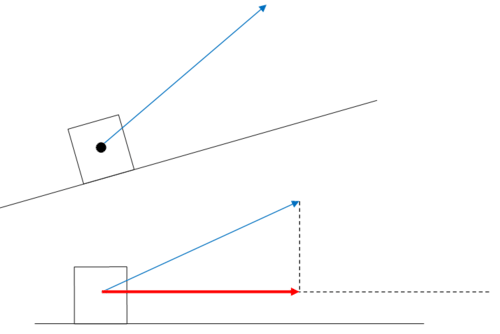
Складові вектора сили батька є,\(\ 100<\cos 39^{\circ}, \sin 39^{\circ}>\) а вектор «на» - це будь-який вектор горизонтально праворуч. Оскільки ми шукаємо лише довжину горизонтальної складової, і у вас вже є кут між двома векторами, скалярна проекція:
\(\ 100 \cdot \cos 39^{\circ} \approx 77.1 \mathrm{lb}\)
Рецензія
- Ескіз векторів\(\ <2,4>\) і\(\ <2,1>\).
- Що таке векторна проекція\(\ <2,4>\) на\(\ <2,1>\)? Намалюйте проекцію.
- Ескіз векторів\(\ <-2,1>\) і\(\ <-1,3>\).
- Що таке векторна проекція\(\ <-1,3>\) на\(\ <-2,1>\)? Намалюйте проекцію.
- Ескіз векторів\(\ <6,2>\) і\(\ <8,1>\).
- Що таке векторна проекція\(\ <6,2>\) на\(\ <8,1>\)? Намалюйте проекцію.
- Ескіз векторів\(\ <1,7>\) і\(\ <6,3>\).
- Що таке векторна проекція\(\ <1,7>\) на\(\ <6,3>\)? Намалюйте проекцію.
- Ящик знаходиться на стороні пагорба, нахиленого на 30 о. Вага коробки - 40 фунтів. Яка величина сили, необхідна для того, щоб ящик не ковзав вниз по гірці?
- Сара знаходиться на санках на стороні пагорба, нахиленого на 60 о. Вага Сари і саней становить 125 фунтів. Яка величина сили, необхідна Сему, щоб утримати Сару від ковзання вниз по пагорбу.
- Автомобіль 1780 фунтів припаркований на вулиці, яка робить кут 15 o з горизонтальним. Знайдіть величину сили, необхідної для того, щоб автомобіль не скотився з гірки.
- Автомобіль 1900 фунтів припаркований на вулиці, яка робить кут 10 o з горизонталлю. Знайдіть величину сили, необхідної для того, щоб автомобіль не скотився з гірки.
- Сила 30 фунтів, яка робить кут 32 o з похилою площиною тягне коробку вгору по площині. Похилу площину роблять кут 20 о з горизонталлю. Яка величина ефективної сили тягне коробку вгору по площині?
- Сила 22 фунтів, яка робить кут 12 o з похилою площиною тягне коробку вгору по площині. Похилу площину роблять кут 25 о з горизонталлю. Яка величина ефективної сили тягне коробку вгору по площині?
- Енн тягне фургон по горизонтальній поверхні з силою 50 фунтів. Рукоятка вагона робить кут 30 о з землею. Яка величина ефективної сили тягне вагона?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.5.
Лексика
| Термін | Визначення |
|---|---|
| скалярна проекція | Скалярна проекція вектора на інший вектор дорівнює довжині проекції першого вектора на другий вектор. |
| одиниця вектор | Одиничний вектор - це вектор з величиною одиниці. |
| векторна проекція | Векторна проекція вектора на заданий напрямок являє собою вектор з величиною, рівною скалярній проекції. Напрямок векторної проекції такий же, як і одиничний вектор даного напрямку. |
Атрибуції зображень
- [Рисунок 1]
Кредит: CK-12 Фонд
Джерело: https://commons.wikimedia.org/wiki/File:Prototype_Pontiac_race_car.jpg
Ліцензія: CC BY-SA