5.2.2: Скалярні прогнози

Скалярні прогнози

Як інженер, або пілот, або водій гоночних автомобілів, або навіть шеф-кухар, часто може бути корисно визначити результат різних величин і напрямків сили, застосованих до певної дії, щоб прийняти рішення про найкраще використання додаткової сили, висоти, швидкості або тепла для досягнення оптимального результату.

Цей урок присвячений скалярним проекціям, які дозволяють робити вищезазначені речі і цілу низку інших.

---

Скалярні прогнози

Скалярна проекція дозволяє досліджувати результат різних «довжин» одного вектора на загальному дослідженні. Проекція вектора на конкретний напрямок, по суті, є результатом застосування конкретного значення в цьому напрямку. Нагадаємо, що точковий добуток вектора - це скалярна величина, що описує тільки величину конкретного вектора. Скалярна проекція задається точковим добутком вектора з одиничним вектором для цього напрямку.

Наприклад, позначення компонентів для векторів, наведених нижче, є AB=⟨4,3⟩ та D = ⟨3, −1.25⟩.

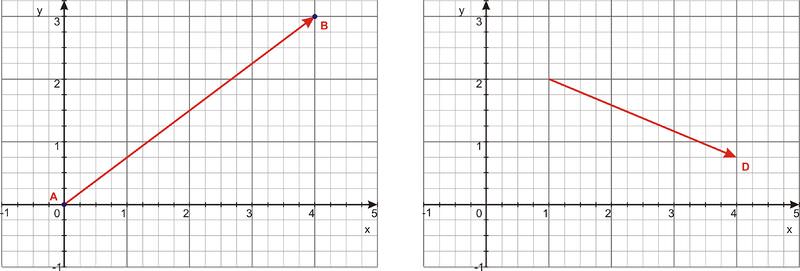
Скалярна проекція вектора AB на\(\ \hat{x}\) задана

\(\ \overrightarrow{A B} \times \hat{x}=(4 \cdot 1)+(3 \cdot 0)+(0 \cdot 0)=4\)

Скалярна проекція вектора AB на\(\ \hat{y}\) задана

\(\ \overrightarrow{A B} \times \hat{y}=(4 \cdot 0)+(3 \cdot 1)+(0 \cdot 0)=3\)

А скалярна проекція вектора AB на\(\ \hat{z}\) задана

\(\ \overrightarrow{A B} \times \hat{z}=(4 \cdot 0)+(3 \cdot 0)+(0 \cdot 1)=0\)

Скалярні проекції AB на напрямки x та y є ненульовими числами, оскільки вектор розташований у площині x-y. Скалярна проекція AB на напрямок z дорівнює нулю, тому що напрямок z перпендикулярно AB.

Векторні проекції

Векторна проекція вектора на заданий напрямок має величину, рівну скалярній проекції. Напрямок векторної проекції такий же, як і одиничний вектор даного напрямку. Нагадаємо, що коли вектор\(\ \vec{v}\) множиться на скаляр s, його складові задаються

\(\ \overrightarrow{s v}=\left\langle s v_{x}, s v_{y}, s v_{z}\right\rangle\)

Для обчислення векторної проекції АВ на напрямок вектора D використовують скалярну проекцію, розраховану в попередньому прикладі, і одиничний вектор\(\ \vec{D}\).

\(\ (\overrightarrow{A B} \times \vec{D}) \vec{D}=\langle(1.23 \cdot 0.923),(1.23 \cdot-0.385)\rangle=\langle 1.135,-0.474\rangle\)

---

Приклади

Приклад 1

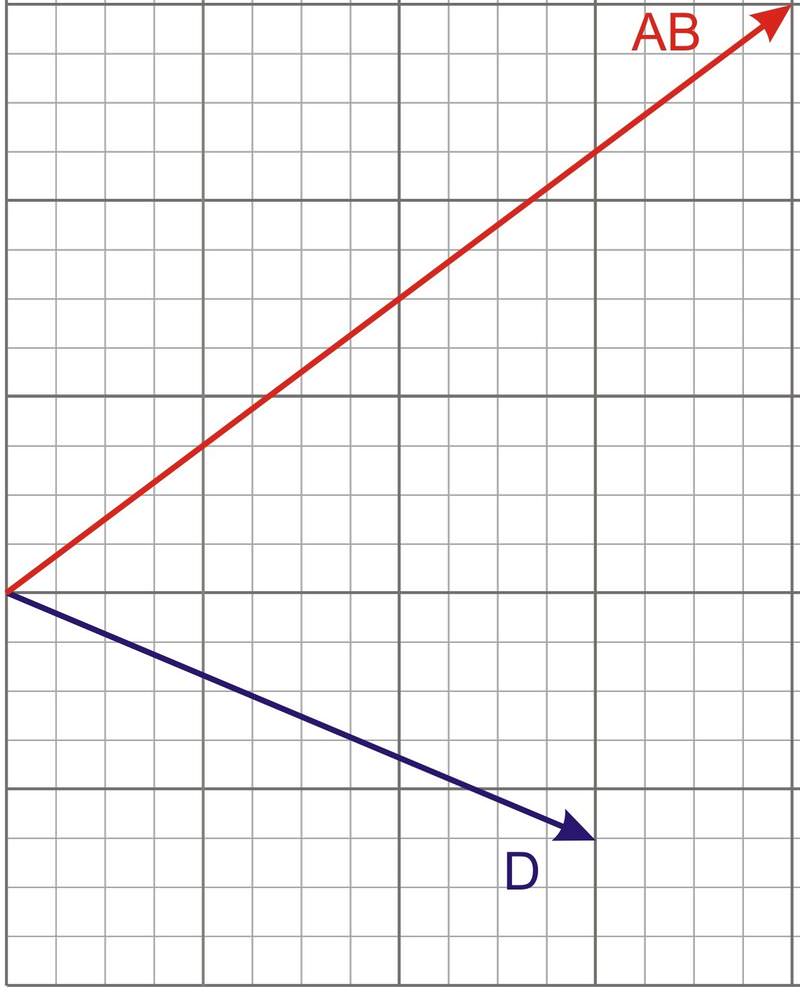
На діаграмі нижче показані обидва вектори AB і D разом на одній сітці. Визначте скалярну проекцію вектора AB на напрямок вектора D.

Рішення

Щоб знайти скалярну проекцію на напрямок іншого вектора, нам потрібно знати одиничний вектор у напрямку вектора D.

По-перше, складовими\(\ \vec{D}\) є

\(\ \vec{D}=\langle 3,-1.25\rangle\)

Тепер величина\(\ \vec{D}\) є

\(\ |D|=\sqrt{\left(D_{x}\right)^{2}+\left(D_{y}\right)^{2}}=\sqrt{3^{2}+(-1.25)^{2}}=\sqrt{9+1.5625}=\sqrt{10.5625}=3.25\)

Нарешті, вектор напрямку\(\ \vec{D}\) є

\ (\\ begin {масив} {l}
\ vec {D} =\ frac {\ vec {D}} {|D|} =\ frac {3\ капелюх {x} + (-1.25)\ капелюх {-1.25}} {3.25}\ капелюх {x} +\ frac {-1.25} {3.25}\ шапка {y}\\
vec {D} =\ лангле 0.923, -0.385\ діапазон
\ end {масив}\)

Тепер ми можемо використовувати точковий добуток для обчислення скалярної проекції АВ на напрямок вектора D.

\(\ \overrightarrow{A B} \times \vec{D}=(3 \cdot 0.923)+(4 \cdot-0.385)+(0 \cdot 0)=2.769+(-1.54)=1.23\)

Приклад 2

Визначити скалярну проекцію вектора\(\ \vec{R}=\langle 27,39,52\rangle\) на напрямок\(\ \vec{T}=\langle 44,26,17\rangle\).

Рішення

Скалярна проекція одного вектора на напрямок іншого є точковим добутком першого вектора з одиничним вектором, що представляє напрямок другого вектора. Для обчислення скалярної проекції нам потрібно визначити одиничний вектор в напрямку вектора\(\ \vec{T}=\langle 44,26,17\rangle\). Пам'ятайте, що одиничний вектор дорівнює відношенню вектора і його величини, тому спочатку потрібно обчислити довжину вектора.\(\ \vec{T}\)

\ (\\ почати {масив} {л}
|\ vec {T} |=\ sqrt {T_ {x} ^ {x} ^ {2} +Т_ {y} ^ {z} ^ {2}} =\ sqrt {(44) ^ {2} + (26) ^ {2} + (17) ^ {2}} =\ sqrt {1936+676+289}\\
=\ sqrt {2901} =53.86\
\ vec {T} =\ frac {\ vec {T}} {|\ vec {T} |} =\ frac {\ лангель 44,26,17\ діапазон} {53.86} =\ лівий\ лангл\ frac {44} {53.86},\ frac {26} {53.86},\ гідророзрив {17} {53.86}\ право\ діапазон =\ лангле 0.8169,0.4827,0.3156\ діапазон
\ кінець {масив}\)

Тепер ми можемо обчислити скалярну проекцію\(\ \vec{R}\) onto,\(\ \vec{T} \) обчисливши точковий добуток

\ (\\ почати {масив} {l}
\ vec {R}\ раз\ vec {T} =( 27\ cdot 0.8169) + (39\ cdot 0.4827) + (52\ cdot 0.3156) =22,0563+18.6253
+16.4112 = 57.0928
\ кінець {масив}\)

Приклад 3

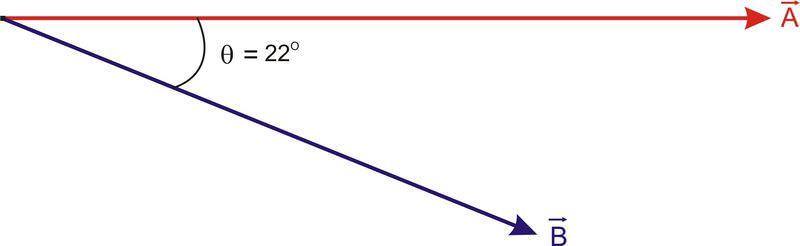
Визначте \(\ \vec{A}\)векторну проекцію на напрямок\(\ \vec{B}\) і\(\ \vec{B}\) векторну проекцію на напрямок\(\ \vec{A} \cdot \vec{A}=7 c m \ @\ 0^{\circ}\) і\(\ \vec{B}=4 c m\ @\ -22^{\circ}\).

Рішення

Векторна проекція одного вектора на напрямок іншого вектора задається\(\ (\vec{A} \times \vec{B}) \vec{B}\) тим, де\(\ \vec{B}\) - одиничний вектор у напрямку\(\ \vec{B}\). Так як це одиничний вектор\(\ \vec{B}\) має величину 1 і має такий же напрямок, як\(\ \vec{B}, \vec{B}=1\ @\ -22^{\circ}\). Тому,\(\ (\vec{A} \times \vec{B}) \vec{B}=(|\vec{A} \| \vec{B}| \cos \theta) \vec{B}=((7)(1) \cos 22)\ @\ -22^{\circ}=6.49\ @\ -22^{\circ}\)

Векторна проекція одного вектора на напрямок іншого вектора задається\(\ (\vec{B} \times \vec{A}) \vec{A}\) тим, де\(\ \vec{A}\) - одиничний вектор у напрямку\(\ \vec{A}\). Так як це одиничний вектор\(\ \vec{A}\) має величину 1 і має такий же напрямок, як\(\ \vec{A}, \vec{A}=1\ @\ 0^{\circ}\). Тому,\(\ (\vec{B} \times \vec{A}) \vec{A}=(|\vec{B}||\vec{A}| \cos \theta) \vec{A}=((4)(1) \cos 22)\ @\ 0^{\circ}=3.71\ @\ 0^{\circ}\)

Приклад 4

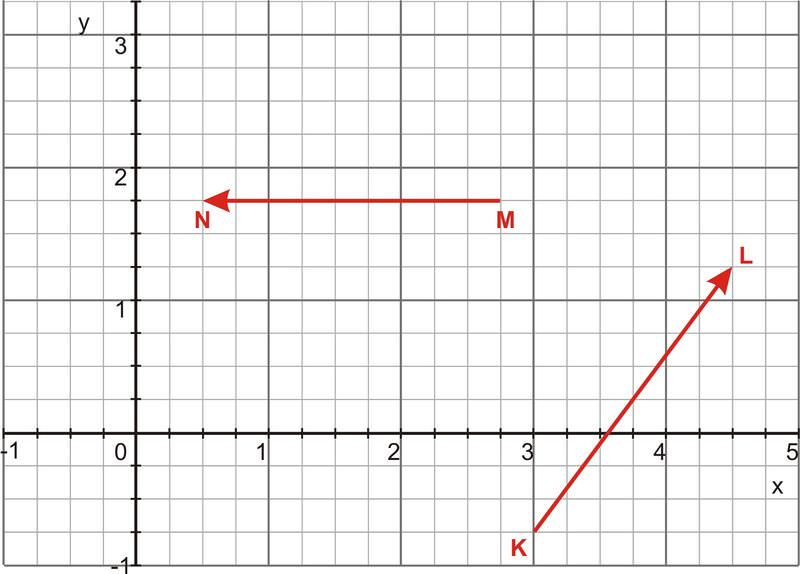
Визначте векторну проекцію вектора\(\ \overrightarrow{M N}\) на вектор\(\ \overrightarrow{K L}\).

Рішення

Векторна прогресія одного вектора на другий вектор - це множення точкових добутків двох векторів і одиничного вектора, що визначає напрямок другого вектора. В даному випадку,\(\ (\overrightarrow{M N} \times \overrightarrow{K L}) \overrightarrow{K L}\). Спочатку нам потрібно визначити складові двох векторів за допомогою інформації, наведеної на графіку. В даному випадку\(\ \overrightarrow{M N}=\langle-2.25,0.0\rangle\) і\(\ \overrightarrow{K L}=\langle 1.5,2,0\rangle\). Потім нам потрібно визначити точковий добуток двох векторів.

\ (\\ почати {масив} {л}
\ переправа стрілка {M N}\ раз\ переправа стрілка {K L} =( М N) _ {x} (K L) _ {x} + (М N) _ {y} (K L) _ {y} + (M N) _ {z} (K L) _ {z}\\
=( 2.25) (1.5) + (2) (0) + (0) (0) =3.375
\ кінець {масив}\)

Нам також потрібно визначити одиничний вектор в сторону\(\ \overrightarrow{K L}\). Пам'ятайте, що одиничний вектор дорівнює відношенню вектора і його величини, тому спочатку потрібно обчислити довжину вектора\(\ \overrightarrow{K L}\).

\ (\\ почати {масив} {л}
|\ переправа стрілка {K L} |=\ sqrt {(K L) _ {x} ^ {2} + (K L) _ {y} ^ {2} + (K L) _ {z} ^ {2}} =\ sqrt {(1.5) ^ {2} + (2) ^ {2} + (0) ^ {2} + (0) ^ {2}} =\ sqrt {2.25+4+0}\\
=\ sqrt {6.25} =2.5
\\ переправа стрілка {K L} =\ frac {\ переправа стрілка {K L}} {|\ переправа стрілка {K L} |} =\ frac {\ кут 1.5,2.0,0\ діапазон} {2.5} =\ лівий\ лангле\ гідророзриву {1.5} {2.5},\ frac {2} {2.5},\ frac {0} {2.5}\ праворуч\ діапазон=\ лангл 0,6,0,8,0\ діапазон
\ кінець {масив}\)

Нарешті, ми помножимо крапковий добуток двох векторів на цей одиничний вектор,

\(\ (\overrightarrow{M N} \times \overrightarrow{K L}) \overrightarrow{K L}=(3.375)\langle 0.6,0.8,0\rangle=\langle 2.025,2.7,0\rangle\)

---

Рецензія

1. Обчислити результат скалярного кратного 6 на векторі\(\ \langle 1,19\rangle\)
2. Обчислити результат скалярного кратного (-8) на векторі\(\ \langle 7,8\rangle\)
3. Обчислити результат скалярного кратного 15 на векторі\(\ \langle-7,3\rangle\)
4. Обчислити результат скалярного кратного (-11) на векторі\(\ \langle-9,20\rangle\)
5. Обчислити результат скалярного кратного 16 на векторі\(\ \langle 9,10\rangle\)
6. Заданий вектор\(\ A=\langle-4,6\rangle\) і вектор\(\ B=\langle 9,15\rangle\). Що таке проекція А на Б?
7. Що таке проекція\(\ \langle 2,10\rangle\) на\(\ \langle 1,3\rangle\)?
8. Заданий вектор\(\ C=\langle 1,2\rangle\) і вектор\(\ D=\langle 1,11\rangle\). Що таке проекція С на D?
9. Заданий вектор\(\ E=\langle-5,3\rangle\) і вектор\(\ F=\langle-1,18\rangle\). Що таке проекція Е на F?
10. Що таке проекція\(\ \langle-2,1\rangle\) на\(\ \langle-5,6\rangle\)?
11. Заданий вектор\(\ \mathrm{H}=\langle 8 i+11 j\rangle\) і вектор\(\ I=\langle-2 i+15 j\rangle\) Що таке проекція H на I?
12. Що таке проекція\(\ \langle-1,6\rangle\) на\(\ \langle 8,16\rangle\)?
13. Що таке проекція\(\ \langle-1,8\rangle\) на\(\ \langle 7,8\rangle\)?
14. Заданий вектор\(\ \mathrm{J}=\langle-4 i+8 j\rangle\) і вектор\(\ K=\langle-8 i+10 j\rangle\). Що таке проекція J на K?
15. Заданий вектор\(\ L=\langle-4,3\rangle\) і вектор\(\ M=\langle 7,17\rangle\). Що таке проекція L на M?

---

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 5.5.

---

Лексика

Термін	Визначення
точковий добуток	Точковий добуток також відомий як внутрішній продукт або скалярний продукт. Дві форми точкового добутку є\(\ \vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta \text { and } \vec{a} \cdot \vec{b}=x_{a} x_{b}+y_{a} y_{b}\).
скалярна проекція	Скалярна проекція вектора на інший вектор дорівнює довжині проекції першого вектора на другий вектор.
блок вектор	Одиничний вектор - це вектор з величиною одиниці.

---

Атрибуції зображень

1. [Рисунок 1]
   Кредит: CK-12 Фонд
   Джерело: https://commons.wikimedia.org/wiki/File:Prototype_Pontiac_race_car.jpg
   Ліцензія: CC BY-SA