4.5: Перевірка обґрунтованості логіки речень

Розібравшись із завданням приборкання природної мови, ми нарешті в змозі виконати другий і третій кроки побудови логіки: визначення логічної форми і розробка тесту на валідність. Тест буде включати застосування навичок, які ми вже вивчили: встановлення таблиць істинності та обчислення істинних значень сполук. По-перше, ми повинні визначити логічну форму в SL.

Логічна форма в SL

Це здасться банальним, але необхідно. Ми вчимося оцінювати аргументи, виражені в SL. Як і будь-яка оцінка дедуктивних аргументів, результат залежить від форми аргументу. Так що таке форма аргументу SL? Розглянемо приклад; ось аргумент в SL:

A aLT B
~B
Отже, ~ A

«A» та «B» означають прості речення англійською мовою; нам байдуже, які саме. Ми працюємо в SL: враховуючи аргумент на цій мові, як ми визначаємо його форму? Досить просто, систематично замінюючи великі літери змінними (малі літери, такі як 'p', 'q' і 'r'). Форма цього конкретного аргументу SL така:

р aLi q
~ q
Отже, ~ р

Заміна великих літер малими змінними була систематичною в цьому сенсі: кожне входження однієї і тієї ж великої літери (наприклад, 'A') було замінено однією і тією ж змінною (наприклад, 'p').

Щоб створити логічну форму аргументу SL, ми систематично замінюємо речення SL на те, що ми будемо називати реченнями. Речення SL - це лише добре сформована комбінація символів SL - великі літери, оператори та дужки. Форма речення - це комбінація символів, яка була б добре сформована в SL, за винятком того, що вона має малі змінні замість великих літер.

Знову ж таки, це може здатися банальним зміною, але це необхідно. Пам'ятайте, коли ми тестуємо аргумент на валідність, ми перевіряємо, чи є його форма такою, що це можливо для його приміщення, щоб виявитися істинним, а його висновок помилковим. Це означає перевірку різних способів заповнення форми конкретними пропозиціями. Змінні - як випливає з назви - можуть відрізнятися в тому, як нам потрібно: вони є загальними і можуть бути замінені будь-яким старим конкретним реченням. Фактичні конструкції SL мають великі літери, які є фактичними реченнями, що мають конкретні істинні значення. Концептуально непослідовно говорити про перевірку різних можливостей для фактичних речень. Тому ми повинні перейти на форми речення.

Перевірка достовірності таблиці істинності

Щоб перевірити аргумент SL на валідність, ми ідентифікуємо його логічну форму, потім створюємо таблицю істинності зі стовпцями для кожної зі змінних і форм речень у вигляді аргументу. Заповнення стовпців Ts і Fs під кожним з операторів у цих формах речень дозволить нам перевірити те, що ми шукаємо: екземпляр форми аргументу, для якого умови виявляються істинними, а висновок виявиться помилковим. Пошук такого екземпляра демонструє недійсність аргументу, а неможливість його знайти демонструє його обґрунтованість.

Щоб побачити, як це працює, корисно буде попрацювати на прикладі. Розглянемо наступний аргумент англійською мовою:

Якщо демократи повернуть Конгрес, буде прийнято багато нових законів.
Демократи не заберуть Конгрес.
Тому багато нових законів не будуть прийняті.

Ми оцінимо його, спочатку переводячи його на SL. Нехай «D» виступає за «демократи забирають Конгрес» і «L» виступають за «Буде прийнято багато нових законів». Це аргумент в SL:

D Це L
~D
Тому ~ Л

По-перше, логічна форма. Замінивши 'D' на 'p' і 'L' на 'q', отримаємо:

р
aCt q ~p
Тому ~ q

Тепер ми створили таблицю істинності, зі стовпцями для кожної зі змінних і стовпцями для кожної з форм речень. Щоб визначити, скільки рядків потрібно нашій таблиці, відзначимо кількість різних змінних, які зустрічаються в аргумент-формі (назвіть це число 'n'); для таблиці знадобиться 2 ⁿ рядків. У цьому випадку у нас є дві змінні - 'p 'і 'q' - і тому нам потрібно 2 ² = 4 рядки. (Якби були три змінні, нам потрібно було б 2 ³ = 8 рядків; якби їх було чотири, 2 ⁴ = 16; і так далі.) Ось таблиця, яку нам потрібно заповнити для цього прикладу:

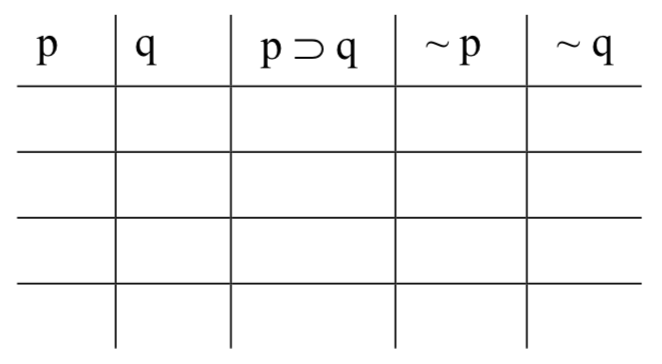
Спочатку заповнюємо «базові стовпчики». Це стовпці для змінних. Робимо це систематично. Почніть з крайнього правого стовпця (у цьому випадку під «q») і заповніть по черзі Ts і Fs: T, F, T, F, F,... стільки разів, скільки вам потрібно - поки ви не отримаєте значення істини в кожному рядку. Це дає нам це:

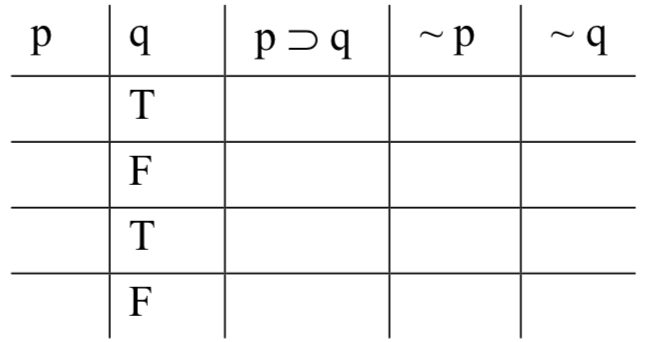
Далі ми переходимо до базового стовпця ліворуч від того, який ми щойно заповнили (під 'p' зараз), і заповнюємо Ts і Fs, чергуючи в два: T, T, F, F, F,... стільки разів, скільки нам потрібно. Результат такий:

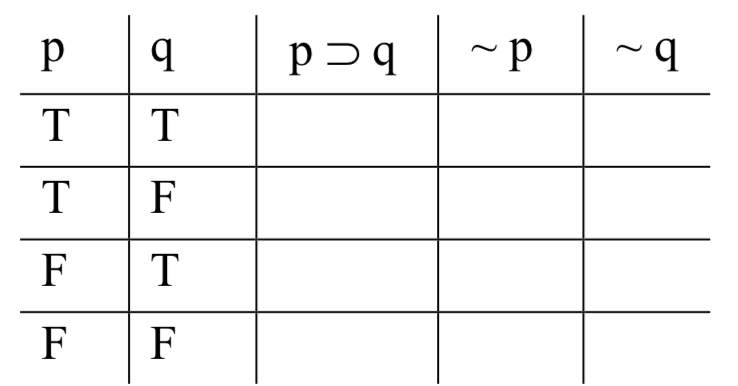
Якби був третій базовий стовпець, ми б заповнили Ts і Fs чергуючи в четвереньках: T, T, T, T, F, F, F, F... Для четвертого базового стовпця ми чергували б кожен інший вісім. І так далі.

Далі нам потрібно заповнити стовпці Ts і Fs під кожним з операторів в стовпцях форм заяви. Для цього ми застосовуємо наші знання про те, як обчислювати істинні значення сполук з точки зору значень їх компонентів, консультуючись з визначеннями таблиць істинності операторів. Ми знаємо, як обчислити значення p tuli q: це брехня, коли р істинно і q false; істинно інакше. Ми знаємо, як обчислити значення ~ p і ~ q: це лише протилежності значень p і q в кожному з рядків. Здійснюючи ці обчислення, ми заповнюємо таблицю таким чином:

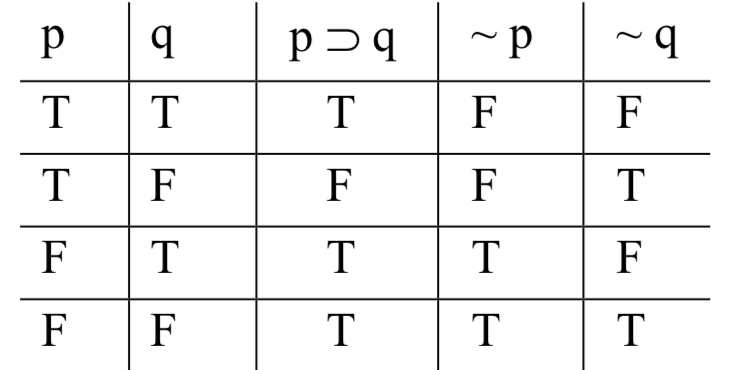
Після заповнення таблиці ми перевіряємо, чи є у нас дійсна або недійсна форма. Позначка недійсної форми полягає в тому, що приміщення може бути істинним, а висновок помилковим. Тут рядки таблиці - це можливості - чотири можливі результати підключення певних речень SL для змінних: обидва true; перше - true, але друге false; перше false, але друге true; обидва false. Причина, по якій ми систематично заповнюємо базові стовпці, як описано вище, полягає в тому, що метод гарантує, що наші рядки будуть колективно вичерпати всі ці можливі комбінації.

Отже, щоб побачити, чи можливо приміщення, щоб збутися, і висновок вийде помилковим, ми перевіряємо кожен з рядків, шукаючи той, в якому це відбувається - той, в якому є T під 'p taLi q', T під '~ p ', і F під '~ q'. А у нас одне: в рядку 3 приміщення збуваються і висновок виходить помилковим. Цього достатньо, щоб показати, що аргумент недійсний:

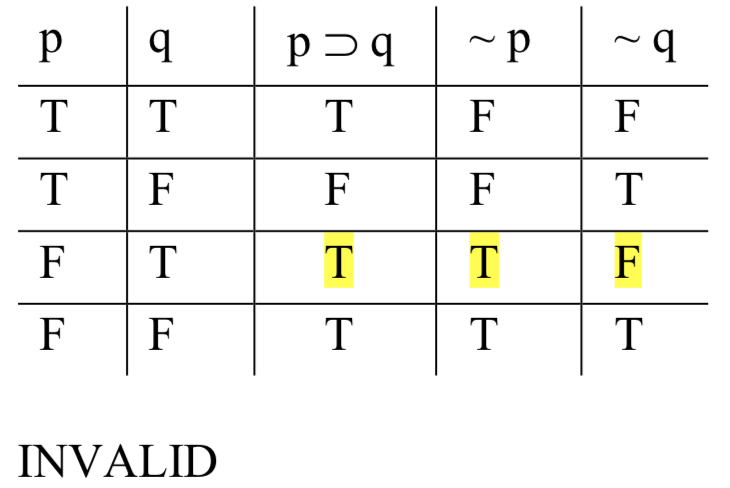
Коли ми перевіряємо на валідність, ми шукаємо одне, і лише одне: рядок (або рядки), в якому приміщення виходять істинними, а висновок виходить помилковим. Якщо ми знайдемо його, ми показали, що аргумент є недійсним. Якщо ми не знайдемо такого, це вказує на те, що приміщення не може бути істинним, а висновок помилковим - і тому аргумент є дійсним. У будь-якому випадку, єдине, що ми шукаємо, - це ряд із справжніми передумовами та помилковим висновком. Будь-який інший вид ряду не має значення. Для початківців часто помилково думають, що вони є. Четвертий рядок в таблиці вище, наприклад, виглядає суттєво. У цьому ряду все виходить правдою. Хіба це не означає щось - щось хороше, наприклад, що аргумент є дійсним? Ні. Пам'ятайте, що кожен ряд представляє можливість; те, що рядок 4 показує, що це можливо для приміщення, щоб бути правдою, а висновок вірним. Але цього недостатньо для обґрунтованості. Щоб аргумент був дійсним, приміщення повинні гарантувати висновок; всякий раз, коли вони правдиві, висновок повинен бути правдивим. Те, що це просто можливо, що всі вони збуваються, недостатньо.

Давайте розглянемо більш цікавий приклад, щоб побачити, як обчислення істинних значень форм заяви іноді має протікати поетапно. Навичка, необхідна тут, не є нічим новим - це лише визначення основних операторів та обчислення значень найпростіших компонентів спочатку, але потрібно пильна увага, щоб все було рівно. Розглянемо цей аргумент SL (не важливо, що його англійський аналог):

(~ А • Б) ∨ ~ Х
Б, To A
Тому ~ Х

Щоб отримати його форму, ми замінюємо 'A' на 'p', 'B' на 'q', а 'X' на 'r':

(~ р • q) ∞ ~ r
q, т.
Отже, ~ r

Таким чином, наша таблиця правди буде виглядати так (вісім рядків, тому що у нас є три змінні; 2 ³ = 8):

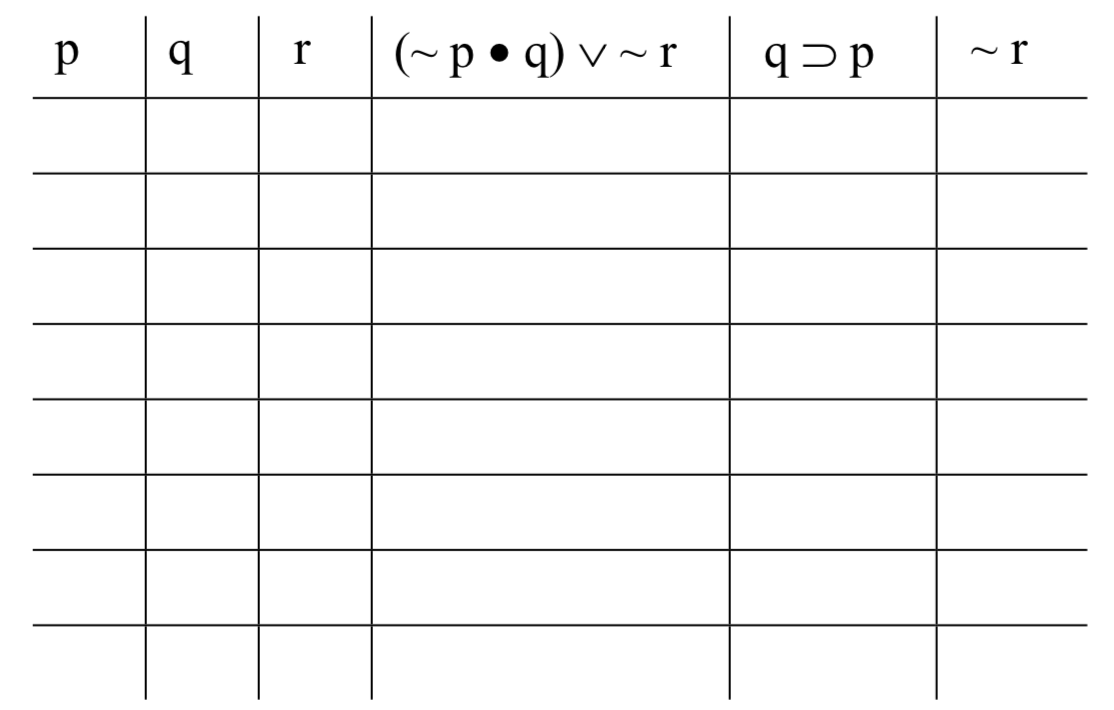
Заповнення базових стовпців, як зазначено вище - чергуючи кожен інший для стовпця під «r», кожні два під «q», а кожні чотири під «p» - ми отримуємо:

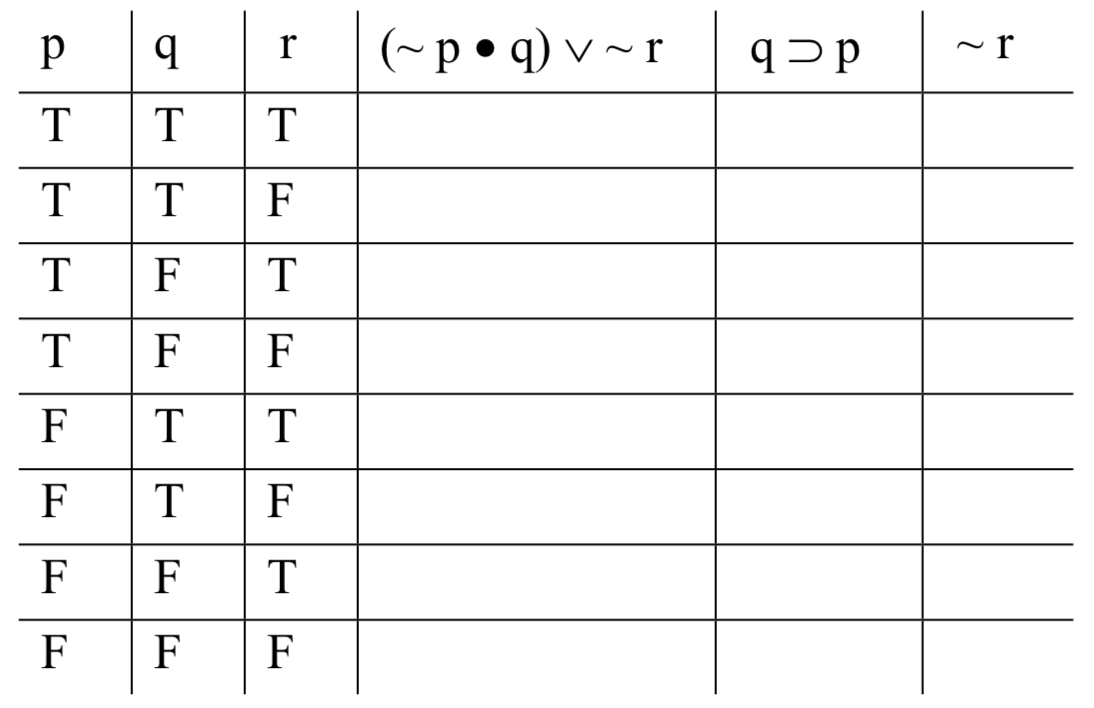
Тепер звернемо увагу на три речення-форми. Почнемо з першої передумови, з'єднання '(~ p • q) ∨ ~ r'. Нам потрібно обчислити істинну величину цієї формули. Ми знаємо, як це зробити, за умови, що у нас є істинні значення найпростіших частин; ми вже вирішили такі проблеми. Єдина відмінність у випадку таблиць істинності полягає в тому, що існує безліч різних присвоєнь істини-значень найпростішим частинам. У цьому випадку існує вісім різних способів присвоєння істинних значень «p», «q» та «r»; вони представлені вісьмома різними рядками таблиці. Отже, ми вирішуємо проблему, яку ми знаємо, як вирішити; ми просто робимо це вісім разів.

Почнемо з визначення основного оператора складової формули. У цьому випадку це клин: у нас є диз'юнкція; лівий диз'юнкт - «(~ p • q)», а правий диз'юнкт - '~ r'. Щоб розібратися, що відбувається під клином в нашій таблиці, треба спочатку розібратися зі значеннями цих складових. Обидва диз'юнкти самі по собі є складними: '(~ p • q)' є кон'юнкцією, а '~ r' є запереченням. Давайте спочатку займемося сполученням. Щоб з'ясувати, що відбувається під крапкою, нам потрібно знати значення '~ p' і 'q '. Ми знаємо значення 'q'; це один з базових стовпців. Ми повинні обчислити значення '~ p'. Це просто: в кожному рядку значення '~ p' буде просто протилежним значенню 'p '. Відзначимо значення під тильдою, оператором, який їх генерує:

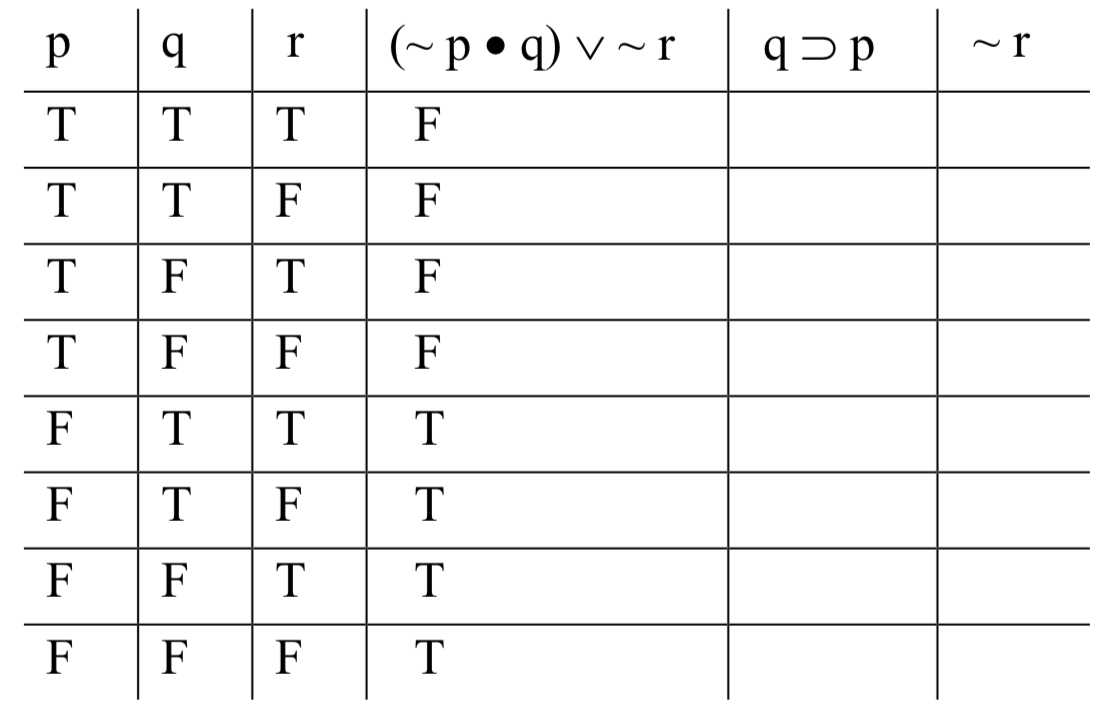
Щоб обчислити значення кон'юнкції, ми розглянемо результат у кожному рядку функції істини для точки, де входами є значення під тильдою в '~ p' і значення під 'q' в базовому стовпці. У рядах 1 і 2 це F • Т; в рядах 3 і 4, F • F; і так далі. Результати:

Колонка, яку ми щойно створили, під крапкою, дає нам діапазон істинних значень для лівого диз'юнкту в першій передумові. Нам потрібні значення правостороннього диз'юнкта. Це просто '~ r', який легко обчислити: це просто протилежне значення 'r' в кожному рядку:

Тепер ми можемо остаточно визначити істинні-значення для всієї диз'юнкції. Обчислюємо значення правди-функції клина, де входами є стовпці під крапкою, з одного боку, а тильда від '~ r' з іншого. F ∨ F, F ∨ Т, F ∨ F і так далі:

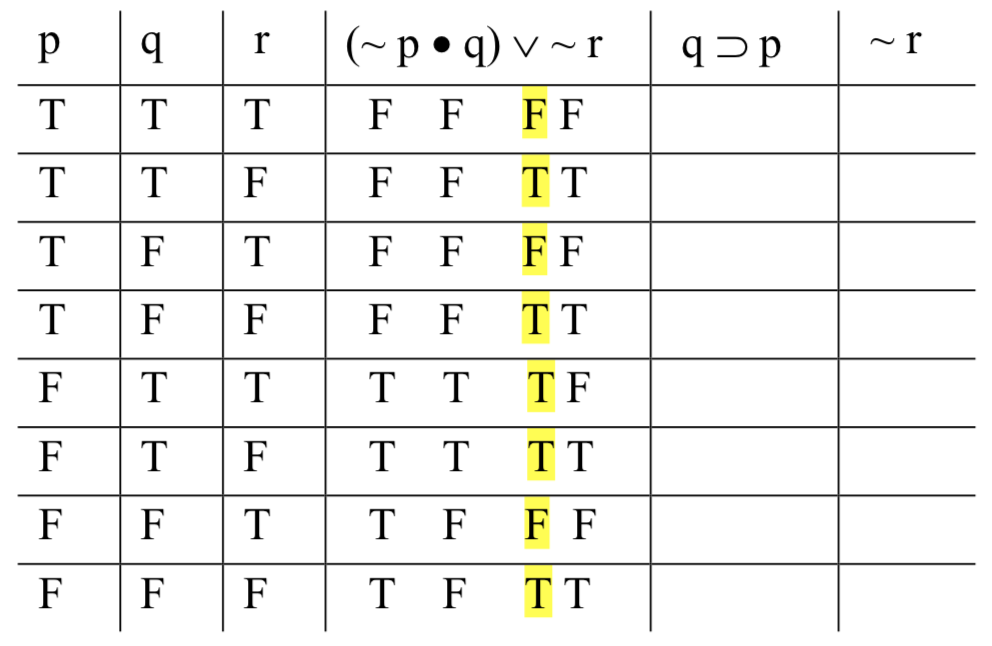
Оскільки цей стовпець представляє діапазон можливих значень для всієї форми речення, ми виділимо його. Коли ми перевіряємо на валідність, ми шукаємо рядки, де приміщення в цілому збуваються; ми будемо шукати значення під їх основними операторами. Щоб зробити це простіше, просто так ми не втрачаємо відслідковувати речі візуально через всі ці стовпці, ми виділяємо один під основним оператором.

Далі, друге приміщення, яке, на щастя, набагато менш складне. Це, однак, трохи складно. Тут нам потрібно обчислити значення умовного. Але зверніть увагу, що речі трохи відрізняються від звичайних: попередній, «q», має свій базовий стовпець праворуч від стовпця для наступного, «р». Це трохи незручно. Ми звикли обчислювати умовні пристрої зліва направо; нам доведеться подумки пристосуватися до того факту, що «q» p' йде справа наліво. (Крім того, якщо це допоможе, ви можете просто відтворити базові стовпці під змінними у стовпці «q» taLi p'.) Таким чином, в перших двох рядках ми обчислюємо T - T; але в рядках 3 і 4 це F | T; в рядках 5 і 6 це T aCL F (єдина обставина, при якій умовні виходять помилковими); an в рядках 7 і 8 це F, це F, L F. Ось результат:

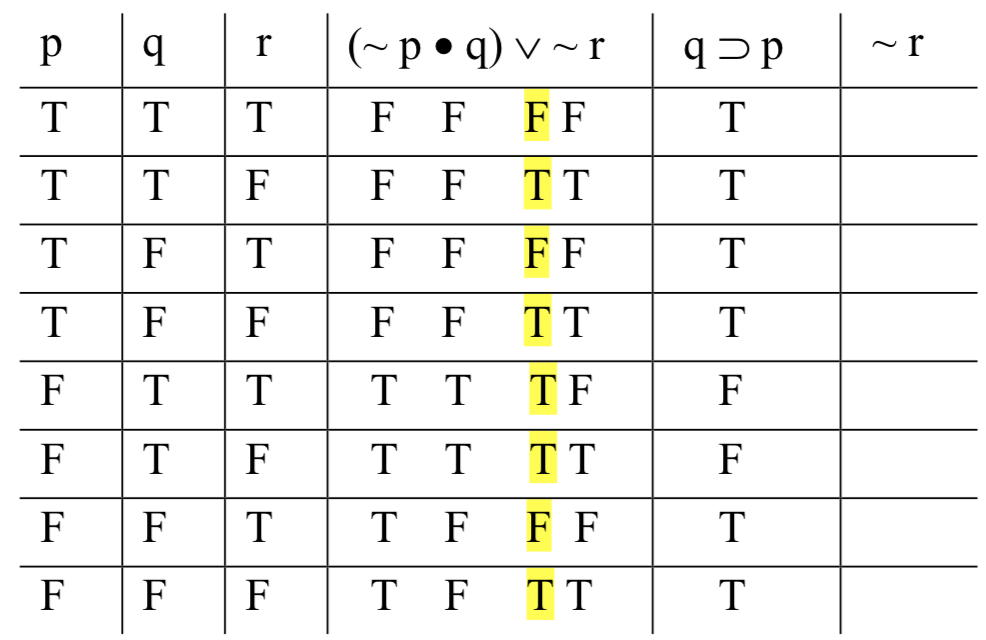
Не потрібно виділяти цю колонку, оскільки це єдиний, який ми створили для цього приміщення, тому не може бути плутанини.

Закінчуємо таблицю обчисленням значень для висновку, що нескладно:

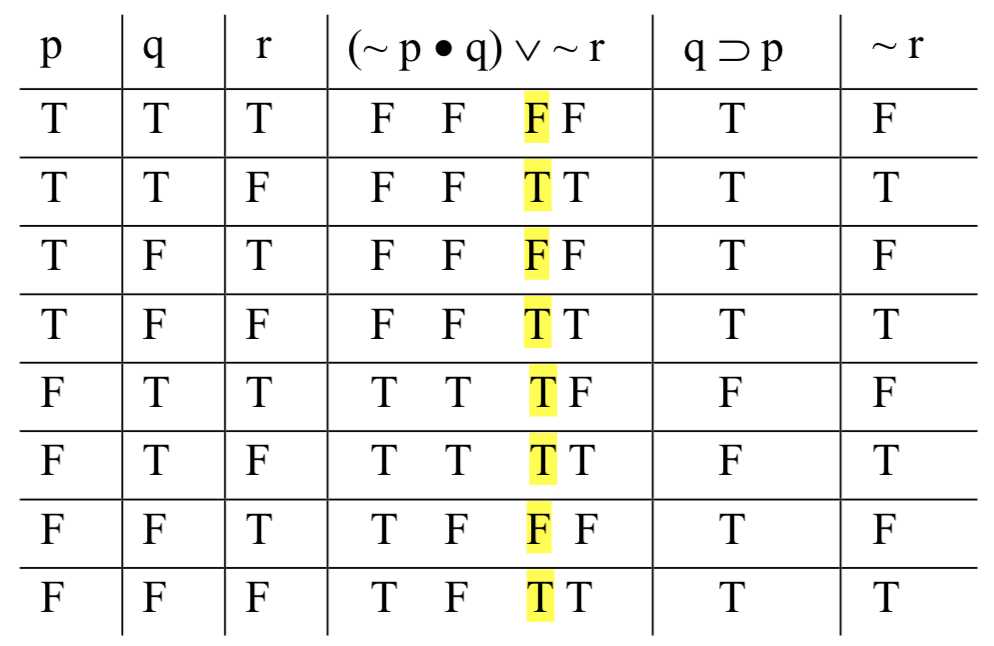
Чи є аргумент справедливим? Шукаємо ряд з істинними передумовами і помилковим висновком. Їх немає. Єдині два ряди, в яких обидва приміщення збуваються, - це другий і восьмий, і в обох ми також маємо вірний висновок. Не можна, щоб приміщення було правдивим, а висновок помилковим, тому аргумент є справедливим.

Так що, як ми перевіряємо аргументи на валідність в SL. Це проста процедура; основним джерелом помилки є проста необережність. Йдіть крок за кроком, уважно стежте за тим, що ви робите, і це повинно бути легко. Варто зазначити, що тест таблиці істинності - це те, що логіки називають «процедурою прийняття рішень»: це процес, керований правилами (алгоритм), який гарантовано відповість на ваше запитання (в даному випадку: дійсний чи недійсний?) в кінцевому числі кроків. Можна запрограмувати комп'ютер для запуску тесту таблиці істинності на довільно довгих аргументах SL. Це втішає, оскільки як тільки один раз отримує більше чотирьох змінних або близько того, процес стає непохитним.

Вправи

Перевірте наступні аргументи на достовірність. Для тих, які є недійсними, вкажіть рядок (и), які демонструють недійсність.

1. ~ A, отже ~ A ∨ B

2. A - В, ~ В, отже ~ A

3. A ∨ B, ~ A, отже ~ B

4. ~ (A ≡ B), A ∨ B, отже A • B

5. ~ (A TRaLS B), ~ B ∨ ~ A, отже ~ (~ A ≡ B)

6. ~ B ∨ A, ~ A, A ≡ B, отже ~ B

7. A aLi (B • C), ~ B ∨ ~ C, отже ~ A

8. ~ A ∞ C, ~ B, ~ C, тому A ≡ C

9. ~ A ∨ (~ B • C), ~ (C ∞ B), тому ~ С | ~ B

10. A ∨ B, B | C, ~ C, отже ~ A