9.13: Обґрунтованість із присудком ідентичності

Last updated
Save as PDF

Page ID: 52943

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Пропозиція\(\PageIndex{1}\)

Природний відрахування з правилами для\(\eq[][]\) - це здорово.

Доказ. Будь-яка формула форми\(\eq[t][t]\) дійсна, так як для кожної структури\(\Struct M\),\(\Sat{M}{\eq[t][t]}\). (Зауважте, що ми припускаємо, що термін\(t\) буде заземлений, тобто він не містить змінних, тому призначення змінних не мають значення).

Припустимо, останній висновок в деривації є\(\Elim{\eq[][]}\), тобто деривація має наступний вигляд:

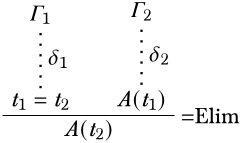
9.13.1.png

Приміщення\(\eq[t_1][t_2]\) і\(A(t_1)\) виведені з нерозряджених припущень\(\Gamma_1\) і\(\Gamma_2\), відповідно. Ми хочемо показати, що\(A(t_2)\) випливає з\(\Gamma_1 \cup \Gamma_2\). Розглянемо структуру\(\Struct{M}\) с\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\). За індукційною гіпотезою,\(\Sat{M}{A(t_1)}\) і\(\Sat{M}{\eq[t_1][t_2]}\). Тому,\(\Value{t_1}{M} = \Value{t_2}{M}\). \(s\)Дозволяти бути будь-якою змінною присвоєння, і\(s'\) бути\(x\) -variant, заданий\(s'(x) = \Value{t_1}{M} = \Value{t_2}{M}\). За пропозицією 5.13.3,\(\Sat[,s]{M}{A(t_1)}\)\(\Sat[,s']{M}{A(x)}\) відф\(\Sat[,s]{M}{A(t_2)}\). З тих пір\(\Sat{M}{A(t_1)}\), у нас є\(\Sat{M}{A(t_2)}\). ◻