7.3: Природний відрахування

Template:MathJaxZach

Природний дедукція - це система деривації, призначена для відображення фактичних міркувань (особливо вид регламентованих міркувань, що використовуються математиками). Фактичне міркування протікає за низкою «природних» закономірностей. Наприклад, доказ випадками дозволяє нам встановити висновок на основі диз'юнктивної передумови, встановлюючи, що висновок випливає з будь-якого з диз'юнктів. Непряме доказ дозволяє встановити висновок, показавши, що його заперечення призводить до протиріччя. Умовний доказ встановлює умовну вимогу «якщо... то...», показуючи, що наслідок випливає з попереднього. Природний дедукція - це формалізація деяких з цих природних висновків. Кожен з логічних зв'язків та кількісних показників поставляється з двома правилами, введенням та правилом усунення, і кожен з них відповідає одному такому природному зразку висновку. Наприклад,$\Intro{\lif}$ відповідає умовним доказом, а$\Elim{\lor}$ доказом у справах. Особливо просте правило$\Elim{\land}$, яке дозволяє робити висновок від$A \land B$ до$A$ (або$B$).

Однією з особливостей, що відрізняє природний відрахування від інших систем деривації, є його використання припущень. Похідний в природному дедукції - це дерево формул. Єдина формула стоїть в корені дерева формул, а «листя» дерева - формули, з яких виводиться висновок. У природному дедукції деякі формули листя відіграють певну роль всередині деривації, але «витрачаються» до того часу, коли деривація дійде до висновку. Це відповідає практиці, в фактичних міркуваннях, введення гіпотез, які залишаються в силі лише на короткий час. Наприклад, у доказі випадків ми припускаємо істинність кожного з диз'юнктів; умовним доказом ми припускаємо істинність попередника; непрямим доказом ми припускаємо істинність заперечення висновку. Цей спосіб введення гіпотетичних припущень, а потім позбавлення від них на службі встановлення проміжного кроку є відмінною рисою природного відрахування. Формули на листках похідного природного відрахування називаються припущеннями, і деякі правила висновку можуть їх «розряджати». Наприклад, якщо ми маємо вихід$B$ з деяких припущень, які включають$A$, то$\Intro{\lif}$ правило дозволяє нам зробити висновок$A \lif B$ і звільнити будь-яке припущення форми$A$. (Щоб відстежувати, які припущення розряджаються, на яких умовиводів, ми позначимо умовивід і припущення, які він розряджає числом.) Припущення, які залишаються нерозрядженими в кінці деривації, разом є достатніми для істинності висновку, і тому висновок встановлює, що його невичерпні припущення тягнуть за собою його висновок.

Співвідношення,$\Gamma \Proves A$ засноване на природному вирахуванні, тримається, якщо є похідне, в якому$A$ є останнє речення в дереві, і кожен лист, який не розряджений, знаходиться в$\Gamma$. $A$це теорема в природному вирахуванні, якщо є похідний, в якому$A$ є останнє речення і всі припущення виписані. Наприклад, ось деривація, яка показує, що$\Proves (A \land B) \lif A$:

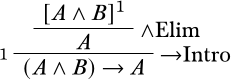
Мітка$1$ вказує на те, що припущення$A \land B$ розряджається при$\Intro{\lif}$ умовиведенні.

Набір$\Gamma$ є непослідовним, якщо$\Gamma \Proves \lfalse$ в природному відрахуванні. Правило$\FalseInt{}$ робить так, що з неузгодженого множини можна вивести будь-яке речення.

Природні системи дедукції були розроблені Герхардом Гентценом та Станіславом Яськовським у 1930-х роках, а пізніше розроблені Дагом Правіцем та Фредеріком Фітчем. Оскільки його висновки відображають природні методи доказування, філософи віддають перевагу. Версії, розроблені Fitch, часто використовуються у вступних підручниках з логіки. У філософії логіки іноді приймалися правила природного дедукції для надання значень логічних операторів («доказово-теоретична семантика»).