7.2: Послідовне обчислення

Last updated
Save as PDF

Page ID: 52709

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Хоча багато систем деривації працюють з домовленостями речень, послідовне обчислення працює з послідовностями. Послідовність - це вираз виду\[A_1, \dots, A_m \Sequent B_1, \dots, B_m,\nonumber\], що представляє собою пару послідовностей пропозицій, розділених послідовним символом\(\Sequent\). Будь-яка послідовність може бути порожньою. Похідний в послідовному численні - це дерево послідовностей, де верхні послідовності мають особливу форму (їх називають «початковими послідовностями» або «аксіомами») і кожна інша послідовність випливає з послідовностей безпосередньо над нею за одним з правил умовиводу. Правила умовиводу або маніпулюють пропозиціями в послідовностях (додавання, видалення, або перестановка їх або зліва, або справа), або вводять складну формулу в висновок правила. Наприклад,\(\LeftR{\land}\) правило дозволяє робити висновок від\(A, \Gamma \Sequent \Delta\) до\(A \land B, \Gamma \Sequent \Delta\), а\(\RightR{\lif}\) дозволяє висновок від\(A, \Gamma \Sequent \Delta, B\) до\(\Gamma \Sequent \Delta, A \lif B\), для будь-якого\(\Gamma\)\(\Delta\), \(A\), і\(B\). (Зокрема,\(\Gamma\) і\(\Delta\) може бути порожнім.)

Відношення, засноване на послідовному\(\Proves\) обчисленні, визначається наступним чином:\(\Gamma \Proves A\) якщо існує певна послідовність,\(\Gamma_0\) така, що кожен\(A\) in\(\Gamma_0\) знаходиться\(\Gamma\) і є похідний з послідовністю \(\Gamma_0 \Sequent A\)на її корені. \(A\)є теоремою в послідовному численні, якщо послідовність\(\Sequent A\) має похідну. Наприклад, ось деривація, яка показує, що\(\Proves (A \land B) \lif A\):

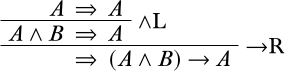
7.2.1.png

Набір\(\Gamma\) є непослідовним у послідовному обчисленні, якщо є похідне\(\Gamma_0 \Sequent\) (де кожен\(A \in \Gamma_0\) знаходиться в,\(\Gamma\) а права частина послідовності порожня). Використовуючи правило\(\RightR{\Weakening}\), будь-яке речення може бути виведено з неузгодженого множини.

Послідовне обчислення було винайдено в 1930-х роках Герхардом Гентценом. Через свою систематичну і симетричну конструкцію, це дуже корисний формалізм для розробки теорії похідних. Відносно легко знайти похідні в послідовному обчисленні, але ці похідні часто важко прочитати, і їх зв'язок з доказами іноді нелегко побачити. Це виявилося дуже елегантним підходом до дериваційних систем, однак, і багато логіки мають послідовні системи числення.