Skip to main content
LibreTexts - Ukrayinska

11.4.3:3-значна логіка

  1. Last updated
  2. Save as PDF
  • Page ID
    52486

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ось старий аргумент під назвою парадокс купи. Почніть з однієї піщинки. Одна піщинка - це не купа піску. Додавання одного зерна до цієї купи також не зробить купу. Насправді додавання однієї піщинки до всього, що не купа, не робить це купи. Так, немає купи піску.

    Але, звичайно, є купи піску, тому з міркуваннями повинна бути певна проблема. У боротьбі з логікою розпливчастості невелика кількість логіків припускають, що повинна бути якась точна точка, де некупа стає купкою. Багато інших рекомендують використовувати те, що ми називаємо 3-значною логікою, щоб дозволити деяким палям бути купи, деякі - не купи, а деякі інші - між ними. Ці логіки рекомендують сказати, що в цих проміжних випадках речення «Це купа» не є ні істинним, ні хибним, і йому має бути присвоєно третє значення істини «ні». Давайте вкажемо цю третю істину значенням символом «#» і присвоїмо його реченню «Додавання однієї піщинки до всього, що не купа, не робить його купи» з тієї причини, що речення не зовсім вірне, але і не зовсім помилкове. Можливо, ми зможемо вирішити парадокс купи таким чином.

    Перш ніж говорити більше про купи, давайте трохи більше розвинемо нашу формальну логіку.

    Що стосується заперечення, наша інтуїція говорить нам, що якщо P скорочували будь-яке формальне твердження, таке як A, B, C,..., або навіть більш складні твердження, що містять багато великих літер, то

    ~P вірно, якщо P є помилковим,

    і ми очікуємо, що таблиця істинності заперечення матиме ці два рядки:

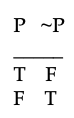
    Знімок екрана 2019-12-25 в 5.17.55 PM.png

    Більшість філософів і логіків цим задоволені. Однак наша інтуїція не настільки зрозуміла, коли мова йде про заперечення речення, яке, на нашу думку, не має класичного значення істини (A T або F). Ось чому. Філософ і логік Бертран Рассел вважав, що всі речення мають класичну істинну цінність, але багато прихильників 3-значної логіки мають інтуїцію, що наступне речення - це ще один вид речення, яке не є ні істинним, ні помилковим:

    Нинішній король Франції лисий.

    Вони кажуть, що це ні правда, ні помилково через невдалу припущення, тому він повинен отримати третє значення істини, таке як #. Кажуть заперечення

    Нинішній король Франції не лисий

    не є істинним або хибним.

    XVII століття король Франції
    король Франції

    Рассел знову не погоджується і каже, що обидва ці речення про короля Франції є помилковими, і вони насправді не є запереченням один одного. Так чи інакше, саме тому прихильники 3-значної логіки дають наступну таблицю для заперечення, де # - третя істина-значення, що означає відсутність класичної істини-значення:

    Знімок екрана 2019-12-25 в 5.20.54 PM.png

    Польський логік Ян Лукасевич використовував цю таблицю в 1924 році, але його мотивацією для розвитку 3-значної логіки було не надавати третю істинну цінність реченням з невдалими припущеннями, ні розпливчастим реченням, а в тому, щоб дати її реченням про майбутнє, наприклад, «Завтра буде морський бій», який він вважали, що були нездатні бути призначені або T або F, тому що завтра не сталося. Інші логіки хочуть використовувати 3-значну логіку для речень про нереальні сутності, такі як «Супермен і Бетмен обідають».

    Щоб мати повну логіку речення, яка є 3-значною, нам потрібно дати таблиці істинності для символів з'єднувача & і v і →. Логіки досліджували різні варіанти цих таблиць. Давайте скористаємося наступними таблицями, які рекомендував Лукасевич.

    Знімок екрана 2019-12-25 в 5.21.27 PM.png

    Спосіб читання цих таблиць для, скажімо, A&B полягає в тому, що істинні значення A походять з одного з рядків, але істинне значення B походить від одного зі стовпців, а значення A&B - це значення, де рядок A відповідає стовпцю B. Наприклад, якщо A - #, а B - F, то дивимося на рядок # і стовпець F і знаходимо, що A&B - це F.

    Вправа\(\PageIndex{1}\)

    Якщо реченню «Нинішній король Франції лисий» дано істинно-значення #, яка істина-значення цих трьох пропозицій при перекладі на нашу 3-значну логіку речень?

    Нинішній король Франції лисий або не лисий.
    Якщо нинішній король Франції лисий, то нинішній король Франції лисий.
    Справа не в тому, що король Франції і лисий, і не лисий.

    Відповідь

    Нехай Б буде пропозиція «Нинішній король Франції лисий». Тоді питання задаються для істинних значень B v ~B і B → B і ~ (B & ~B). Їх значення зобов'язані таблицями істинності бути # і T і #.

    Вправа\(\PageIndex{1}\)

    Розглянемо більш загальне питання про те, як працює 3-значна логіка. Чи можете ви з тим, як закон Аристотеля виключений середній P v ~ P тримається в класичній 2-значній логіці, але не в нашій 3-значній логіці? Закон передбачає, що незалежно від того, яке значення істини має речення, замінене на P, складне речення P v ~P матиме значення істини Т. Чому цей підтекст тримається в 2-значній логіці, але не вдається в нашій 3-значній логіці?

    Відповідь

    Коротко, закон виключеного середнього провалюється в 3-значній логіці, оскільки, коли P отримує значення #, більша пропозиція P v ~P не відповідає дійсності; це #.

    Попередня перевірка концепції показала, що P v ~P є тавтологією в нашій 2-значній логіці, але не може бути тавтологією в нашій 3-значній логіці, як ми очікували. Лукасевич хотів, щоб він зазнав невдачі, коли P був реченням, не вистачало класичної правдивої цінності, наприклад, «Завтра буде морський бій».

    Давайте тепер перейдемо від одиночних речень до аргументів. Ми визначаємо аргумент, який буде дедуктивно дійсним у двозначній або 3-значній логіці тоді і лише тоді, коли його висновок вірний, коли його передумови є істинними. Аргументи в 3-значній логіці можна оцінювати за допомогою таблиць істинності подібно до звичайної 2-значної логіки, але тепер рядків більше, оскільки є більше комбінацій істинних значень. Наприклад, якщо аргумент складається з пропозицій рівно з двох букв пропозиції A і B, то замість чотирьох рядків класичних таблиць істинності є дев'ять рядків. Вам знадобляться наступні дев'ять рядків для того, щоб розглядати всі можливі призначення істини-значень реченню букв А і Б:

    Знімок екрана 2019-12-25 в 5.23.45 PM.png

    Давайте використаємо таблиці істинності, щоб вирішити, чи є наступна форма аргументу дійсною в нашій 3-значній логіці. Він дійсний у 2-значній логіці і, як кажуть, має логічну форму під назвою «modus ponens».

    Знімок екрана 2019-12-25 в 5.24.17 PM.png

    Ось таблиця істинності для цього аргументу в нашій 3-значній логіці:

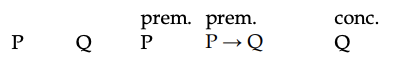
    Знімок екрана 2019-12-25 в 5.24.47 PM.png
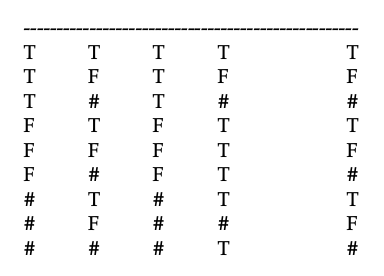
    Знімок екрана 2019-12-25 в 5.25.17 PM.png

    Щоб використовувати цю таблицю для оцінки обґрунтованості аргументу, ви будете шукати рядок, який служить контрприкладом аргументу, а саме рядок, в якому два передумови є істинними, але висновок не є. Є тільки один ряд, в якому два приміщення вірні, перший ряд, тому вам не потрібно дивитися на інші ряди. У цьому першому рядку Q отримує значення T, тому рядок не може бути контрприкладом. Тому аргумент справедливий в 3-х значній логіці. Однією з моралів тут є те, що якщо ви зосередитеся в цій проблемі на пошуку лише зустрічного прикладу, вам не потрібно будувати цілу таблицю істинності дев'яти рядків; достатньо побудувати лише перший рядок. Зазвичай при розгляді будь-якого аргументу буде певний спосіб впорядкувати полювання на контрприклад і уникнути побудови великих таблиць.

    Вправа\(\PageIndex{1}\)

    Показати, що цей класично дійсний аргумент є недійсним у нашій 3-значній логіці:

    А → Б так ~А в Б

    Відповідь

    У рядку, в якому A і B обидва отримують значення істини #, передумова вірна, але висновок не є, так що рядок є контрприкладом