Skip to main content
LibreTexts - Ukrayinska

11.4.2: Аргументи, логічні наслідки та контрприклади

  1. Last updated
  2. Save as PDF
  • Page ID
    52497

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Перейдемо від семантики пропозицій до семантики аргументів. Аргумент у Sentential Logic вважається дійсним або логічно правильним на всякий випадок, якщо висновок повинен бути істинним, коли передумови істинні. Коли це справа з деяким аргументом, ми говоримо, що його висновок є логічним наслідком його приміщення. Ось вагомий аргумент:

    А → Д
    А
    —
    Д

    Ось рецепт або механічний метод для прийняття рішення про те, чи є аргумент дійсним. Перевірте таблицю істинності для всіх пропозицій в аргументі (а саме всі її передумови плюс його висновок). Якщо у всіх ситуаціях (тобто всі рядки, або всі присвоєння істинних значень на великі літери), які роблять приміщення істинними, висновок також робиться вірним, то аргумент оголошують дійсним. В іншому випадку оголосіть його недійсним. Давайте застосуємо метод до цієї таблиці істинності для наведеного вище аргументу:

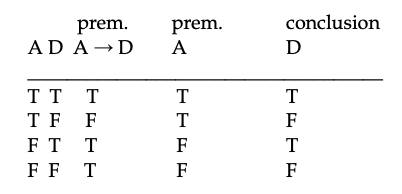
    Знімок екрана 2019-12-25 в 5.15.27 PM.png

    Будь-який аргумент, написаний у формальній Sentential Logic, може бути перевірено на достовірність цим методом побудови та перевірки таблиць істинності. Некоректний аргумент матиме рядок, який показує, як все приміщення може бути істинним, а висновок помилковий.

    Вправа\(\PageIndex{1}\)

    Використовуйте метод таблиці істинності, щоб перевірити, чи є цей аргумент дійсним.

    ~А
    С → А
    —
    ~С

    Відповідь

    Так, він дійсний. Він має форму модуля tollens. Немає можливості, щоб приміщення було правдивим, поки висновок є помилковим, не порушуючи таблиць істини.

    У вагомому аргументі немає рядка таблиці істинності, в якій приміщення отримують Ts, тоді як висновок отримує F. Тобто, вагомі аргументи не мають контраприкладів. Зверніть увагу, що вагомі аргументи можуть мати помилкові передумови.

    Вправа\(\PageIndex{1}\)

    Чи є у цього аргументу контрприклад?

    А → Б
    Б
    —
    А

    Відповідь

    Так. Цей аргумент має недійсну форму, яка називається підтвердженням послідовності. У ситуації, коли A є помилковим, а B є істинним, ми маємо контрприклад, оскільки тоді аргумент має істинні передумови та помилковий висновок. Наприклад, ось аргумент, який вчиняє помилку ствердження наслідку: якщо той хлопчик, який стоїть там, є вашим дідусем, то цей хлопчик - чоловік. Цей хлопчик - самець. Отже, той хлопчик, що стоїть там, - твій дідусь. Це має справжні передумови та помилковий висновок у будь-якій ситуації, коли там стоїть хлопчик. Оскільки існує ситуація, навіть якщо це не ситуація в реальному житті, яка зробила б приміщення істинним, а висновок помилковим, аргумент є недійсним.